Диаграмма Вейча функции y
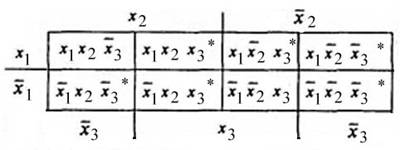
После выделения конъюнкций (они отмечены звездочкой), видно, какие конъюнкции могут образовывать пары для склеивания.
В результате применения операций склеивания и поглощения можно получить другое аналитическое выражение:
в котором отсутствуют возможности дальнейших склеивании и поглощений. Однако последнее выражение является избыточным, так как отдельные конъюнкции могут быть “липшими”, т.е. их “составные части” могут включаться в другие конъюнкции. У данной функции существует пять безызбыточных дизъюнктивных форм, из которых только две являются минимальными:
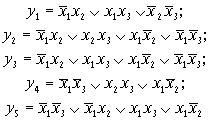
Из приведенных зависимостей видно, что только функции у1 и у4 являются минимальными формами функций, так как они содержат наименьшее число конъюнкций и имеют минимальный ранг этих конъюнкций.
Минимизация “вручную” возможна только для функций, зависящих от 4-5 переменных, так как трудоемкость переборов растет в квадратичной зависимости от числа переменных. Применение мощных ЭВМ для этих Целей позволяет расширить границы до п= 12-15. Если при этом учесть, что функции могут быть частично определены (значения функций на некоторых наборах переменных можно определять произвольно), а также что иногда приходится решать задачи совместной минимизации систем ЛФ, то минимизация ЛФ становится сложной инженерной, практической и научной проблемой.
Техническая интерпретация логических функций
По логическим выражениям проектируются схемы ЭВМ. При этом следует придерживаться следующей последовательности действий.
1. Словесное описание работы схемы.
2. Формализация словесного описания.
3. Запись функций в дизъюнктивной (конъюнктивной) совершенной нормальной форме по таблицам истинности.
4. Минимизация логических зависимостей с целью их упрощения.
5. Представление полученных выражений в выбранном логически полном базисе элементарных функций.
6. Построение схемы устройства.
7. Проверка работоспособности полученной схемы. Покажем взаимосвязь перечисленных этапов на примере.
Пример 7. Спроектировать схему, фиксирующую появление “неправильной” тетрады в двоично-десятичном представлении чисел.
1. Каждая тетрада двоично-десятичного представления числа содержит десятичные цифры 0-9, что соответствует двоичным числам 0000-1001. Значения тетрады, соответствующие двоичным числам 1010-1111 (шестнадцатеричные цифры A-F), не должны появляться при представлении десятичных чисел.
2. Составим таблицу истинности функции (табл. 2.8), которая принимает значения, равные единице, при появлении “неправильных” тетрад. Разряды тетрады обозначим переменнымих, у, z, u.
Таблица 1.6
Таблица истинности функции F
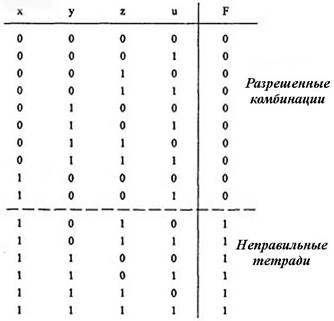
3. Исходная совершенная дизъюнктивная нормальная форма записывается
4. Эта форма функции допускает упрощение, что видно по диаграмме Вейча (табл.1.7). Этот же результат может быть получен аналитически.
Таблица 2.9
Диаграмма Вейча для функции f
5. Минимальная форма функции F в логически полном базисе {&, v, } будет иметь вид:
Для представления этой же схемы в другом полном базисе, например {&}, воспользуемся правилом де Моргана:
6. По полученным зависимостям можно построить схемы фиксации “неправильных” тетрад (рис.1.8).
7. Проверить работоспособность построенных схем можно путем задания различных комбинаций переменных х, у, z, и и определения реакции на выходе схемы F.
Рис. 1.8 Схема фиксации неправильных тетрад: а - схема в базисе (Г, &, V), б - схема в базисе (&).
Техническая реализация логических функций
Булева алгебра допускает множество логических операций, но всего трех из них — И, ИЛИ, НЕ — достаточно для того, чтобы выразить любые логические операции, или функции.
Так, с помощью одного элемента ИЛИ на два входа, двух элементов И на два входа и одного элемента НЕ можно построить логическую схему двоичного полусумматора (рис. 1.9), способного осуществлять операцию двоичного сложения двух одноразрядных двоичных чисел (т. е. выполнять правила двоичной арифметики):
0 + 0 = 0; 0+1 = 1; 1 + 0=1; 1 + 1 = 0.
Рис.1.9. Логическая схема двоичного полусумматора
При этом полусумматор выделяет бит переноса. Однако такая схема не содержит третьего входа, на который можно подавать сигнал переноса от предыдущего разряда суммы двоичных чисел. Поэтому полусумматор используется только в младшем разряде логической схемы суммирования многоразрядных двоичных чисел, где не может быть сигнала переноса от предыдущего двоичного разряда. Полный двоичный сумматор (рис. 1.10) складывает два многоразрядных двоичных числа с учетом сигналов переноса от сложения в предыдущих двоичных разрядах.
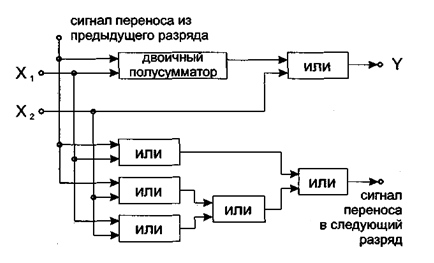
Рис.1.10. Логическая схема двоичного сумматора
Соединяя двоичные сумматоры в каскад, можно получить логическую схему сумматора для двоичных чисел с любым числом разрядов. С некоторыми изменениями эти логические схемы применяются для вычитания, умножения и деления двоичных чисел. С их помощью построены арифметические устройства современных компьютеров.
Все описанные логические схемы являются однотактными. Значения их выходов однозначно определяются значениями их входов. Фактор времени в них отсутствует. Наряду с ними существуют многотактные логические схемы, в которых значения их выходов определяются не только значениями их входов, но и их состоянием в предыдущем такте. Фактор времени и определяется этими тактами. К таким логическим схемам относятся схемы памяти (рис. 1.11). Они строятся с помощью обратной связи с выхода на вход логической схемы.
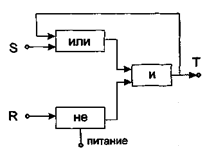
Рис. 1.11. Логическая схема оперативной памяти
Даже простейшая логическая схема памяти на один бит обязательно содержит обратную связь с выхода на вход. Она состоит из трех логических элементов, реализующих логические функции НЕ (отрицание), И, ИЛИ.
В этой схеме с помощью обратной связи образуется замкнутая цепь с выхода на вход для запоминания входного сигнала. Эта цепь сохраняется после снятия входного сигнала неограниченное время, вплоть до появления сигнала стирания.
Такая схема памяти имеет еще и другое название: триггер с раздельными входами — для запоминания (5) и стирания (R). Широко используется в вычислительной технике и триггер со счетным входом. Он имеет только один вход и один выход. Такая схема осуществляет деление на 2, т. е. состояние ее выхода изменяется только после подачи подряд двух входных импульсов. Соединяя триггеры со счетным входом в последовательный каскад, можно осуществлять деление на 2, 4, 8, 16, 32, 64 и т. д.
Схема оперативной памяти играет важную роль при построении систем управления машинами повышенной опасности, такими, как прессы и одноножевые бумагорезательные машины («гильотины») (рис. 1.12). Чтобы обезопасить руки оператора, такие машины строят с системами двуручного управления. Подобные системы заставляют оператора держать обе руки на кнопках управления во время каждого рабочего цикла машины. Это исключает попадание рук в опасную зону, где происходит прессование детали или резание стопы бумаги.
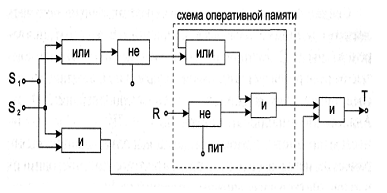
Рис. 1.12. Логическая схема безопасного двуручного управления машинами повышенной опасности
Приведенный пример еще раз показывает, насколько, казалось бы, абстрактная наука алгебра логики близка к практической жизни. Она позволяет решать самые разные задачи управления.
Входные и выходные сигналы электромагнитных реле, подобно высказываниям в булевой алгебре, также принимают только два значения. Когда обмотка обесточена, входной сигнал равен нулю, а если по обмотке протекает ток, входной сигнал равен единице. Когда контакт реле разомкнут, выходной сигнал равен нулю, а если контакт замкнут, выходной сигнал равен единице.
Именно это сходство между высказываниями в булевой алгебре и поведением электромагнитных реле заметил известный физик Пауль Эренфест. Еще в 1910 г. он предложил использовать булеву алгебру для описания работы релейных схем в телефонных системах. По другой версии идея использования булевой алгебры для описания электрических переключательных схем принадлежит Ч. Пирсу. В 1936 г. основатель современной теории информации Клод Шеннон в своей докторской диссертации объединил двоичную систему счисления, математическую логику и электрические цепи.
Связи между электромагнитными реле в схемах удобно обозначать с помощью логических операций НЕ, И, ИЛИ, повторения (ДА) и т. д. Например, последовательное соединение контактов реле реализует логическую операцию И, а параллельное соединение этих контактов — логическую операцию ИЛИ. Аналогично выполняются операции И, ИЛИ, НЕ в электронных схемах, где роль реле, замыкающих и размыкающих электрические цепи, выполняют бесконтактные полупроводниковые элементы — транзисторы, созданные в 1947—1948 гг. американскими учеными Джоном Бардином, Уильямом Шокли и Уолтером Браттейном.
В современных компьютерах микроскопические транзисторы в кристалле интегральной схемы сгруппированы в системы «вентилей», выполняющих логические операции над двоичными числами. Так, с их помощью построены описанные выше двоичные сумматоры, позволяющие складывать многоразрядные двоичные числа, производить вычитание, умножение, деление и сравнение чисел между собой. Логические «вентили», действуя по определенным правилам, управляют движением данных и выполнением инструкций в компьютере.