Лекция 10 Числовые характеристики случайного вектора.

1. Математическое ожидание.

Пусть задан случайный вектор . Математическим ожиданием случайного вектора называется.

Для непрерывных случайных величин

(8)

. ( 9)

Для дискретных случайных величин

, (10)

(11)

в которых суммирование проводится по всем возможным значениям индексов и.

Если множество возможных значений случайного вектора конечно, то математические ожидания случайных величин ив формулах представляют собой конечные суммы. В случае счетного множества возможных значений случайного вектора математические ожидания в этих формулах равны суммам числовых рядов, если эти ряды абсолютно сходятся. В противном случае математическое ожидание случайного вектора не определено.

2. Условные математические ожидания. Линии регрессии.

Рассмотрим совокупность тех точек на плоскости, для которых случайная величина принимает постоянное значение. Математическое ожидание для такой совокупности точек называется условным математическим ожиданием

линия регрессии по. (12)

Аналогично для совокупности тех точек на плоскости, для которых случайная величина принимает постоянное значение

–линия регрессии по. (13)

3. Характеристики рассеяния.

Дисперсия случайной величины

(14)

Эту формулу можно представить в следующем виде

(15)

Аналогично

(16)

(17)

Среднеквадратичное отклонение для случайных величин иравно.

, .

4. Характеристики связи случайных величин

Корреляционным моментом или ковариацией двух случайных величин называется математическое ожидание произведения отклонений этих величин от их математического ожидания

. (18)

В дальнейшем будем использовать обозначение .

Для непрерывных случайных величин

(19)

Для дискретных случайных величин

(20)

где – вероятность того, что случайный векторпримет значение.

Размерность корреляционного момента равна произведению размерностей случайных величин.

Безразмерной характеристикой связи случайных величин является коэффициент корреляции

.

Дисперсия случайной величины является ковариацией ее с собой, т.е.

,,

Если и– независимые случайные величины, то их корреляционный момент равен нулю. Действительно, в этом случае . Поэтому

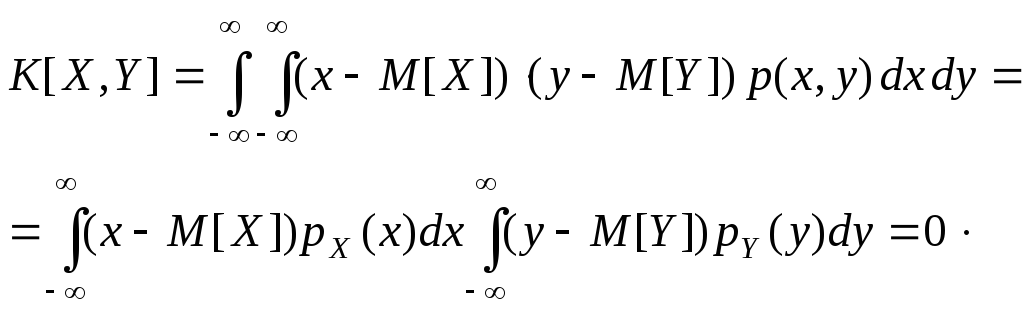
Здесь было учтено, что

, .

Обратное утверждение неверно. Из равенства нулю корреляционного момента системы случайных величин ине следует, что эти величины независимы.

Пример.

Покажем, что существуют зависимые случайные величины, для которых . Пусть

Тогда плотности распределения случайных величин иравны соответственно

, .

Отсюда видно, что , т.е.и– зависимые случайные величины. Вычислим корреляционный момент этих случайных величин по формуле

Найдем вначале математические ожидания случайных величин

Здесь внутренний интеграл равен нулю как интеграл от нечетной функции по симметричному относительно промежутку.

Аналогично . Следовательно,

.

Случайные величины называются некоррелированными, если их корреляционный момент равен нулю и коррелированными, если их корреляционный момент не равен нулю.

Если случайные величины инезависимы, то они некоррелированы.

Если случайные величины изависимы, то они могут быть коррелироваными и некоррелироваными.

Если случайные величины инекоррелированы, то они могут быть зависимыми и независимыми.

Если случайные величины икоррелированы. то они зависимы.

Матрицей ковариаций случайных величининазывается симметричная квадратная матрица второго порядка, на главной диагонали которой расположены дисперсии случайных величини, а на побочной диагонали – корреляционные моменты, т.е.

. (21)