Содержание

1. Понятия случайных величин и их свойства	3
2. Основные понятия теории случайных функций	10
3. Понятия случайных полей	14
4. Список литературы	17

1. Понятия случайных величин и их свойства.

Одним из важнейших основных понятий теории вероятностей является понятие о случайной величине.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее какое именно.

Различают случайные величины прерывного (дискретного) и непрерывного типа.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений прерывной случайной величины бесконечно.

Также различают зависимые и независимые случайные величины.

Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины X и Y называются зависимыми.

Условно будем обозначать случайные величины большими буквами, а их возможные значения – соответствующими малыми буквами.

Про случайную величину будем говорить, что она подчинена закону распределения.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.; его можно задать таблично, аналитически (в виде формулы) и графически.

Установим форму, в которой может быть задан закон распределения прерывной случайной величины X. Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности. Такую таблицу будем называть рядом распределения случайной величины X.

Для наглядности закон распределения случайной величины можно изобразить графически: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Затем в этой прямоугольной системе координат строят точки (x_i,p_i) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения:

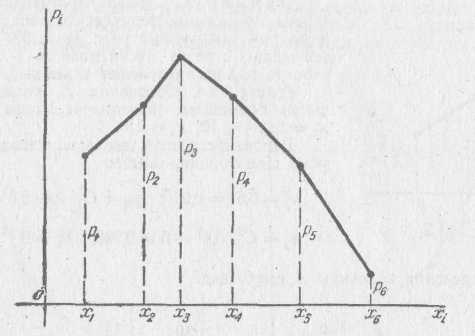
Многоугольник распределения, так же как ряд распределения, полностью характеризует случайную величину.

Каждый закон распределения представляет собой некоторую функцию, и указание этой функции полностью описывает случайную величину с вероятностной точки зрения.

Итак, выше мы ввели в рассмотрение ряд распределения как исчерпывающую характеристику (закон распределения) прерывной случайной величины. Однако эта характеристика не является универсальной; она существует только для прерывных случайных величин. Для непрерывной случайной величины такой характеристики построить нельзя. Следовательно, для непрерывной случайной величины не существует ряда распределения, в том смысле, в каком он существует для прерывной величины. Для количественной характеристики этого распределения введем понятие функции распределения случайной величины X.

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее x, т.е.

F(x) = P(X<x).

Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки x.

Иногда функцию распределения называют интегральной функцией или интегральным законом распределения.

Функция распределения – самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как прерывных, так и непрерывных.

Однако, этот способ задания не является единственным. Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности.

Плотность распределения непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x):

f(x) = F'(x).

Иногда функцию f(x) называют дифференциальной функцией распределения или дифференциальным законом распределения величины X.

Термин «плотность распределения» становится особенно наглядным при пользовании механической интерпретацией распределения; в этом смысле функция f(x) буквально характеризует плотность распределения масс по оси абсцисс. Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.(рис.2)

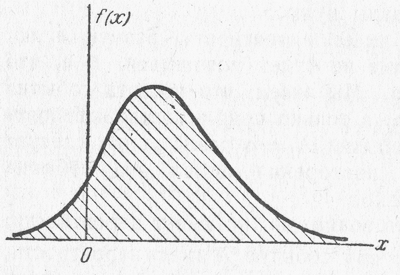
рис.2

Итак, мы познакомились с рядом полных, исчерпывающих характеристик случайных величин – так называемых законов распределения. Такими характеристиками были:

для дискретной случайной величины

1. функция распределения;

2. ряд распределения (графически – многоугольник распределения);

для непрерывной величины

1. функция распределения;

2. плотность распределения (графически – кривая распределения).

Также для случайных величин существуют числовые характеристики, назначение которых – выразить в сжатой форме наиболее существенные особенности распределения.

Среди числовых характеристик случайных величин нужно прежде всего отметить те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.

Важнейшую роль среди этих характеристик играет математическое ожидание случайной величины, которое иногда его называют просто средним значением случайной величины.

Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

.

С механической точки зрения, математическое ожидание M[X] есть не что иное, как абсцисса центра тяжести данной системы материальных точек.

Заметим, что в вышеприведенной формулировке определение математического ожидания справедливо только для дискретных случайных величин.

Для непрерывной величины X математическое ожидание выражается уже не суммой, а интегралом:

,

где f(x) – плотность распределения величины X.

Выше мы рассмотрели формулы, выражающие математическое ожидание соответственно для прерывной и непрерывной случайной величины X.

Если же величина X принадлежит к величинам смешанного типа, то ее математическое ожидание выражается формулой вида:

,

где сумма распространяется на все точки x_i, в которых функция распределения терпит разрыв, а интеграл – на все участки, на которых функция распределения непрерывна.