11067

110

равных исходному (см. рис.90) Теорема верна для паркетов, набранных на основе любого произвольно взятого треугольника.

Рис.93. Паркет набранный на основе произвольно взятого неправильного четырехугольника.

Триангуляция Делоне, по имени советского математика Бориса Делоне, является как бы трехмерным паркетом, набранным из треугольников, создана для приближенного моделирования и математического описания топологии местностей в первой пол. XX в., оказалась удобна для моделирования лендморфных объектов архитектуры. Представляется собой разновидность паркета из неравновеликих треугольных элементов– полигональную модель поверхности либо разрезку плоскости, формирующуюся по определенным правилам.

Плоские и трехмерные сетки, вплотную связанные с классификацией и типологией соответствующих плоскостей, поверхностей и объемов. Пионером по использованию в архитектуре эстетики сетчатых структур является русский химик и инженер В. Шухов, далее на идею трехмерного моделирования на основе неортогональных сетчатых структур наталкивались в разное время Отто Фрай, лауреат Прицкеровской премии, Р.Б. Фулер, Н. Форстер (см. таб.18.)

Таблица 18.

111

112

Градостроительные кластеры, при всей сложности их планировочной организации в основе формально-композиционной структуры, имеют градостроительную сетку некоторого геометрического вида.

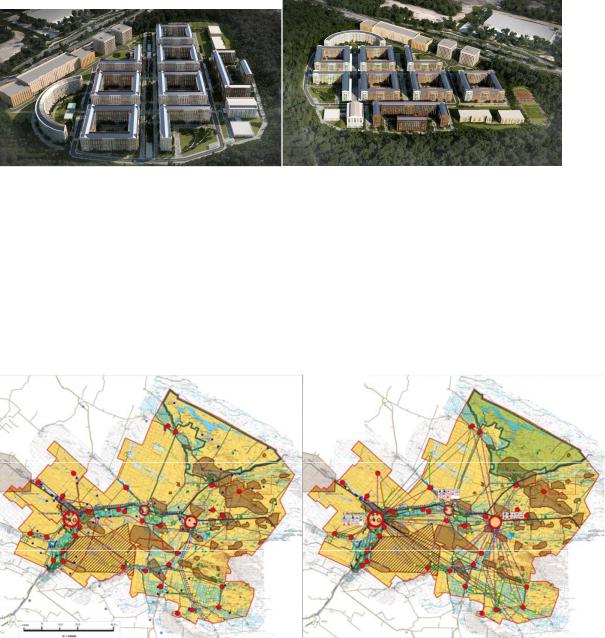
Рис. 94. Испанский архитектор Рикардо Бофилл разработал для российской группы компаний "СУ-155" проект жилой недвижимости - Media City, более 3,5 тыс. квартир площадью около 145 тыс. кв. м. Реализована идея замкнутых кварталов с изолированными от внешнего шума внутренними дворами, разделенными внутриквартальными проездами. Подобная планировка создает закрытые от уличного движения дворы, более уютные и комфортные для жителей.

Кла́стер (cluster — скопление, кисть, рой) — объединение нескольких однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определёнными свойствами.

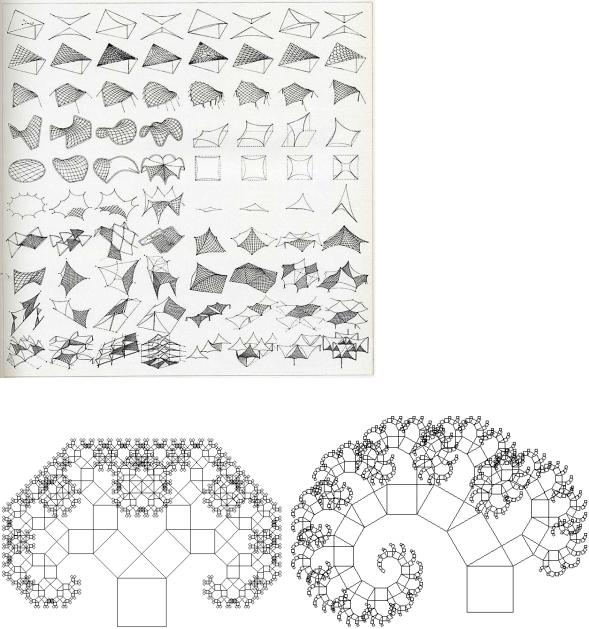
Рис. 95. Структура градостроительного кластера промышленного характера : градостроительная на основе комбинирования и трасформации градостроительных сеток, структура кластера с наложенным графом функциональных взаимосвязей.

Сингулярный — лат. singularis отдельный, странный, особенный; в физике точка, в которой уравнения имеют особенность:

113

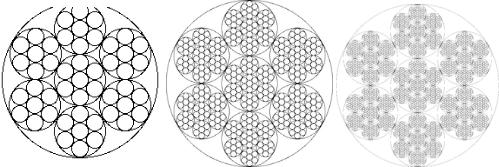
Рис.96. Штудии сетчатых поверхностей Фрай Отто. Casabella 301 1966, 35.

Рис. 97. Дерево Пифагора — разновидность фрактала, основанная на фигуре, известной как «Пифагоровы штаны». Одно из доказательств теорему приводит фигуру, где сторонам прямоугольного треугольника построены смежные квадраты. Дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку. Одним из свойств дерева Пифагора является то, что если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице. В классическом дереве Пифагора угол равен 45 градусам, можно построить дерево Пифагора при использовании других углов, т. н. обдуваемое ветром дерево Пифагора.

Алгоритм построения «дерева Пифагора» сводится к рекурсивному построению отрезков под определенными углами 45, 30 и 60 градусов. Если изображать только отрезки, соединяющие каким-либо образом выбранные «центры» треугольников, получится «обнаженное» дерево Пифагора. Повторение алгоритма построения на каждом уровне фрактала называется итерацией, и подлежит математическому описанию в виде формулы.

114

Рис. 98. Круговой фрактал после третьей итерации, после четвёртой итерации, после пятой итерации.

Лекция 8.

систематическом изложении геометрии точка обычно принимается заодно из исходных понятий. В современной математике, топологии точками

пространстве точкой на зывается некая упорядоченная совокупность из n чисел. В теории множеств точки характеризу ют свойства рассматриваемого множества.

При этом, понятие точки представляет собой одну из величайших научных абстракций, и даже мистификаций т.к. физически точек не существует. Об этом косвенно свидетельствует принцип неопределенности Гейнзенберга – определить точное местоположение действительно малой элементарной частицы невозможно в силу волновой природы вещества. Конкретным местоположением будет область пространства, облако математических точек. Учитывая открытие складок пространства– времени, гравитационн ых волн, становится понятной условность не точки, а даже самого пространства. В природном формообразовании ни один объект в приближении не может являться точкой - все и меет размеры и структуру, пылинка в воздухе, звезда в миллионах световых лет от Земли, самолет в десятках километров от наблюдателя и пчела на р асстоянии пяти метров, причем структура каждой «точки» вовсе не обязательно сводится к центрической – шару, кругу. Квадрат Малевича, подвешенный в крупном выставочном зале с бел ыми стенами и светом на расстоянии пятидесяти метров будет выглядеть, как точка. Следовательно, лю бая точка при приближении может демонстрировать усложнение, некомпактность собственной композиционной структуры. С точки зрения иерархии мерности, созданной а Винчи на основе геометрии Евклида, точка

115

нольмерна. Зная сущностную невозможность точки, можно смело охарактеризовать точку, как нольмерное пространство.

По принадлежности геометрические точки подразделяются на особые точки: точки линий (ТЛ), точки поверхностей (ТП) и точки объемов (ТО).

В группе ТЛ выделяются следующие блоки точек.

1.Точки прямых линий: точка отграничения линии (точка начала и конца отрезка прямой, точка середины отрезка); точка пересечения n – го числа линий (зона пересечения); точка деления отрезка линии на части; точка изменения толщины линии.

2.Точки кривых линий: гладкая точка кривой (в которой можно провести единственную касательную линию); точка касания (в которой можно провести единственную касательную); точка перегиба (здесь касательная пересекает кривую); точка возврата 1-го и 2-го рода (с расположением по обе стороны оси и по одну сторону); точка излома (кривая в этой точке имеет две касательные, что свойственно строфоиде и декартову листу); точки min и max кривизны (кривизна – К плоской кривой в данной точке является величина, обратная радиусу соприкасающейся окружности: К=1/r). Помимо этих точек здесь можно отметить: фокусную точку, центральную точку, точку вершины и сопряжения (скачкообразного изменения кривизны).

Рис. 99.

Точки кривых линий (по рукописи

Голова Г.М.).

116

3.Точки ломаных линий: точки перелома (изменения направления развития, поворота); точки смыкания (соединение отдельных разнонаправленных отрезков).

4.Точки пучковых линий представляются одной точкой – точкой исхода.

Рис.100. Точки ломаных и пучковых линий (по рукописи Голова Г.М.).

В группе ТП можно обозначить следующие блоки точек.

1. Точки плоских поверхностей являют собой точки плоских решеток всех видов (регулярных и нерегулярных, сквозных и центрических тригональных, гексагональных, тетрагональных, октогональных и т.д.). Они фиксируют пространственные габариты решеток, их конфигуративность и подразделяются на: наружные (контурные) и внутренние (внутриконтурные) точки.

Рис. 101. Точки плоских решеток (по рукописи Голова Г.М.)

117

Сюда же относятся замечательные точки треугольников, ч асть из которых используется при триангуляции в проектировании топологических

структур:

Рис. 102. Слева направо: А). Точка пересечения биссетрисцентр вписанной окружности. Б).Точка пересечения медиан является центром тяжести треугольника. В). Точка пересечения высот называется ортоцентром треугольника.

В 1765 году немец ий математик Эйлер доказал, что в любом треугольнике ортоцентр, центр тяжести и центр описанной окружности лежат на одной прямой, названой позже прямой Эйлера.

Рис.103. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной в округ треугольника окружности. В 20 х гг. XIX века французские математики По нселе, Брианшон и другие установили независимо друг от друга следующую теорему: основания медиан, основания высот и середины отрезков высот, соединяющих ортоцентр с вершинами треугольника, лежат на одной и той же

окружности.

2.Точки криволинейных поверхностей характеризуют также как и в первом случае, точк и криволинейных решеток всех видов. Они определяют своим местоположением тот или иной вид поверхности и подразделяются на контурные, внутриконтурные и точки вершин (конус).

3.Точки складчатых поверхностей такие же, как в первом случае, но с дополнением в виде к онтактных точек вдоль линии сты ковки плоских элементов складчатой поверхности.

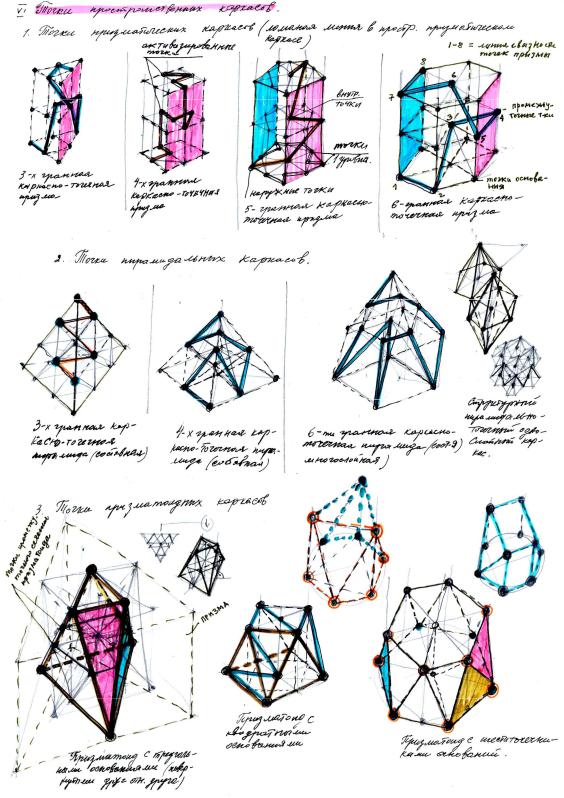
Рис.104.

Составные

точечные каркасы.

(по рукописи Голова Г.М.)

119

Специфичность понятия архитектурной точки заключается в том, что она может быть представлена как продукт выполнения операций свертывания или развертывания исходной формы.

В первом случае исходной формой может быть одномерное (Л), двухмерное (П) или трехмерное образование (О). Их сжатие (свертывание) в пределах одинакового фона (поля восприятия) определяет получение составных точек: линейных точек (ЛТ), а не точек линий; поверхностных (ПТ) и объемных точек (ОТ). При этом, сжатие представляется как уменьшение габаритов, при сохранении общей структуры исходной формы, как перевод ее на более низкий уровень восприятия. При этом визуальная масса полученной сжатием (свертыванием) формы существенно меньше визуальной массы исходной формы. Архитектурные точки могут быть простыми (моноконтурными) и сложными (поликонтурными).

Рис.106. Виды комбинаторных точек (по рукописи Голова Г.М.).

Идеальная простая точка («прототочка») представляет собой результат свертывания круга или шара. Графически она визуализируется одним действием – нажатием остро заточенного инструмента (иглы, карандаша) и характеризуется наличием простого контура. Однако, точка может быть получена и несколькими действиями – короткими перемещениями инструмента в любых направлениях. При переводе ее на другой уровень восприятия (операция развертывания), определяющий второй случай ее представления, увеличенный контур представляется как сложный. Совокупность информативных точек этого контура свидетельствует о том, что перед нами точечная точка (ТТ). Контур являет собой линейную точку (ЛТ). Расчленение внутреннего поля «мнимыми» динамическими осями позволяет считать ее поверхностной точкой (ПТ), а при развитии ее структуры по оси Z она выступает как объемная точка (ОТ). Таким образом, нам открывается алгоритм процесса построения объемной формы путем постадийного развертывания исходной точечно-точечной формы до получения конечного продукта – точечно-объемной формы. Он может быть поливариантным в зависимости от исходных условий – замысла автора. В кодированном виде данный алгоритм выглядит следующим образом: ТТ, ЛТ, ПТ, ОТ, а это ни что иное как результат