
10298
.pdf
которые будем называть комплексными. Число x Re z Re(x iy) назы-
ваютдействительной (лат. realis– действительный) частью комплексного числа, а число y Im z Im(x iy) его мнимой (лат. imaginarius – мнимый)
частью.
31.2. Геометрическая интерпретация комплексных чисел. Ком-
плексные числа удобно изображать точками плоскости xOy , с декартовой
системой координат, которую в этом случае называют комплексной плоскостью. Ось абсцисс этой плоскости называют действительной осью – ей отвечают действительные числа z x , а ось ординат – мнимой осью. Числа z iy , лежащие на мнимой оси, называют чисто мнимыми.
Два комплексных числа z1 x1 iy1 и z2 x2 iy2 равны тогда и только
тогда, когда x1 x2 и y1 y2
Сопряжённым к данному комплексному числу z x iy назовем число z x iy , которое обычно помечается чертой сверху. Сопряжённые комплексные числа отличаются знаком мнимой части. Если z x iy , то z x iy . Сопряжённые числа симметричны относительно действительной оси (см. рис. 31.1).
Рис. 31.1
31.3.Тригонометрическая форма комплексного числа. Наряду с ал-
гебраической формой комплексного числа z x iy |
введем его тригоно- |
метрическую форму. Будем интерпретировать |
комплексное число |
z x iy как радиус-вектор точки (x, y) .Модулем r |
комплексного числа |
|
|
|
|
z x iy называют длину этого вектора r | z | x2 |
y2 (см. рис. 31.2). Мо- |
||
дуль – это расстояние от начала координат до точки |
z (x, y) . |
||
Угол между положительным направлением оси Ox и радиус-векто- ром z называется аргументом комплексного числа. Поскольку этот угол определяется с точностью до числа, кратного 2 ,то выделим его главную ветвь 0 argz 2 . Значение arg z определяется как решение системы уравнений
220

cos |
|
|
x |
|
; sin |
|
|
y |
|
; 0 |
2 . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
x2 |
y2 |
x2 |
y2 |
|||||||||
|
|
|
|
|
|
|
|
Рис. 31.2
От алгебраической формы комплексного числа легко перейти к его тригонометрической форме
|
|
z x i y r cos ir sin r(cos i sin ) . |
|
||||||||||||||||||||||
Пример.Представить число |
|
|
z 1 i в тригонометрической форме. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Модуль r |
|
1 i |
|
|
( 1)2 ( 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 . Аргумент находим, выбирая из |
||||||||||||||||||||||
решений уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
cos |
|
1 |
|
|
|
|
2 |
; |
sin |
|
1 |
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
||||||
то, которое попадает в промежуток |
|
|
0 2 . |
Это угол |
5 |
2250 (см. |
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||
рис. 31.2). Таким образом,
z1 i 
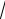 2(cos 54 i sin 54 ) .
2(cos 54 i sin 54 ) .
31.4.Операции над комплексными числами. Начнем со сложения. Суммой (разностью) двух комплексных чисел z1 x1 iy1 и z2 x2 iy2
называется комплексное число z z1 z2 (x1 x2 ) i( y1 y2 )
Рис. 31.3
221

Заметим, что это соответствует правилу сложения векторов (см. рис. 31.3).
Произведением комплексных чисел называется число
(x1 iy1 ) (x2 iy2 ) (x1x2 y1y2 ) i(x1 y2 x2 y1 ) .
Найдём произведение двух комплексных чисел, заданных в тригонометрической форме
z1 z2 r1 (cos 1 i sin 1 ) r2 (cos 2 i sin 2 )
r1 r2 (cos 1 cos 2 sin 1 sin 2 i(sin 1 cos 2 cos 1 sin 2 ))
r1r2 (cos( 1 2 ) i(sin( 1 2 )) .
Таким образом, при умножении комплексных чисел в тригонометрической форме их модули нужно перемножить, а аргументы сложить.
Геометрический смысл умножения на комплексное число
z r(cos i sin )
состоит в том, что происходит «растяжение» плоскости с коэффициентом r и поворот на угол . Благодаря этим свойствам комплексных чисел с их помощью удаётся решать задачи теории упругости, связанные с деформацией твёрдых тел, а также изучать движение жидкостей и газов.
Пример.Найти произведение чисел z1 2(cos(30 i sin30 ) и
z2 2(cos(120 i sin120 ).Умножение в тригонометрической форме даёт
z z |
2 |
4(cos(1500 |
i sin1500 ) 4( |
3 i 1) 2 |
3 2i . |
|||||||||
1 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
150 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Рис. 31.4 |
|
|
|
|
|
|||
|
|
|
210 |
|
|
|
|
|
|
|
|
330 |
|
|
|
|
|
|
240 |
222 |
|
|
|
300 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
270 |
|
|
|
|
|
|
|
В результате умножения вектора z1 на вектор z2 длина вектора z1 уве-
личилась в два раза и он «повернулся» на угол 120 (см. рис. 31.4).
После этого становится понятными правила умножения отрицательных чисел. Почему, например, ( 1) ( 1) 1? Действительно, представляя
1 в тригонометрической форме, получаем
( 1)( 1) (cos i sin ) (cos isin ) (cos 2 isin 2 ) 1.
Также перестаёт быть «таинственной» формула i 2 1, поскольку
i i (cos 2 i sin 2 )(cos 2 i sin 2 ) (cos i sin ) 1.
Чтобы получить частное двух комплексных чисел, нужно умножить и числитель и знаменатель дроби на число сопряжённое знаменателю и отделить вещественную и мнимую части.
z |
z1 |
|
x1 iy1 |
|
(x1 iy1)(x2 iy2 ) |
|
x1x2 y1 y2 |
i |
x2 y1 x1 y2 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z |
2 |
|
x iy |
2 |
|
(x iy |
2 |
)(x iy |
) |
|
x2 |
y2 |
|
x2 |
y2 |
||
|
|
|
2 |
|
2 |
2 |
2 |
|
2 |
2 |
2 |
2 |
|
|||||
Найдём частное двух комплексных чисел, заданных в тригонометрической форме
z1 |
|
r1 (cos 1 |
i sin 1 ) |
|
r1 |
(cos |
i sin )(cos |
|
i sin |
) |
|
|
|
|
2 |
||||||
z2 |
|
r2 (cos 2 |
i sin 2 ) |
|
r2 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
r1 (cos 1 cos 2 sin 1 sin 2 i(sin 1 cos 2 cos 1 sin 2 )) r2
r1 (cos( 1 2 ) i sin( 1 2 )). r2
Итак, модуль частного двух комплексных чисел равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
|
|
|
|
|
|
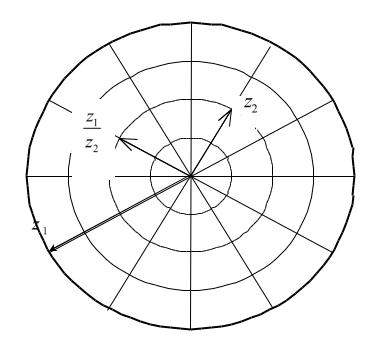
Пример.Найти частное чисел z1 2 |
3 2 i и |
z2 1 i 3 . Пред- |
|||
ставим каждое из этих чисел в тригонометрической форме:
z 4(cos2100 |
isin 2100 ) , |
z |
2 |
4(cos600 |
i sin 600 ) . |
1 |
|
|
|
|
Тогда частное равно z1 / z2 2(cos1500 i sin1500 ) 
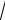 3 i (см. рис. 31.5).
3 i (см. рис. 31.5).
223
|
|
90 |
120 |
|
60 |
|
3 |
|
150 |
2 |
30 |
|
||
|
1 |
|
180 |
|
0 |
210 |
330 |
240 |
300 |
|
Рис. 31.5 |
Определим операцию возведения в степень комплексного числа. По правилу умножения комплексных чисел в тригонометрической форме для всякого натурального числа n имеем
zn rn (cos n i sin n ) .
В частном случае, когда модуль числа равен единице, получается формула, носящая имя английского математика А. Муавра (1667-1754)
(cos i sin )n cos n isin n .
Эта формула служит источником для получения многих замечательных соотношений, связывающих тригонометрические функции. Например, при n 2 имеем равенство
cos2 2isin cos sin2 cos2 isin 2 .
Приравнивая действительные и мнимые части, получаем известные формулы для синуса и косинуса двойного аргумента
cos2 cos2 sin2 , |
sin 2 2sin cos . |
224

Лекция 32. Решение алгебраических уравнений
32.1. Извлечение корня из комплексного числа.Число z называется корнем n -ой степени из комплексного числа a , если zn a . Эта опера-
ция – обратная возведению комплексного числа в целую положительную степень. Во множестве вещественных (действительных) чисел эта задача
равносильна задаче нахождения корней уравнения |
xn a 0 и мы решали |
|||
её, раскладывая многочлен xn a |
на множители. Иногда это удавалось. |
|||
Например, уравнение x2 4 0 |
даёт два корня |
x |
2 , а уравнение |
|
|
|
|
1,2 |
|
x2 1 0 корней не имеет. |
|
|
|
|
|
Итак, пусть дано комплексное число a | a | (cos i sin ) и уравне- |
|||
ние |
zn a . Будем искать корни этого уравнения среди комплексных чи- |
|||
сел, |
выраженных в тригонометрической форме |
z r(cos i sin ) , r ? , |
||
? В этой форме уравнение примет вид
rn (cos i sin )n | a | (cos isin )
или
rn (cos n i sin n ) | a | (cos isin ) .
Два комплексных числа в тригонометрической форме равны тогда и только тогда, когда их модули равны, а аргументы отличаются на число, кратное 2 , т.е.
rn | a |, n 2 k, k 0, 1, 2, .
Поэтому все корни имеют один и тот же модуль r n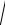 | a | , а аргументы этих корней определяются по формуле
| a | , а аргументы этих корней определяются по формуле
|
|
|
2 |
k, |
k 0, 1, 2, . |
|
|
||||
|
n |
|
n |
|
|
Убедимся, что число корней конечно и равно показателю n степени уравнения. Действительно, представляя искомые корни в тригонометрической форме
|
|
|
|
|
|
2 |
|
|
|
2 |
|
, |
|
|
|
|
|
|
|
||||||||
zk |
n | a | cos( |
|
|
|
k) i sin( |
|
|
|
k) |
||||
n |
n |
n |
n |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
видим, что в силу периодичности тригонометрических функций достаточно
ограничиться значениями k 0, 1, 2, |
, n 1. Если k целое отрица- |
|||
тельное, то мы не получим новых корней, так как |
|
|||
z k zn k , |
k 1, 2, |
, n 1. |
|
|
В этом легко убедиться, прибавив 2 к значению аргумента корня |
z k , что |
|||
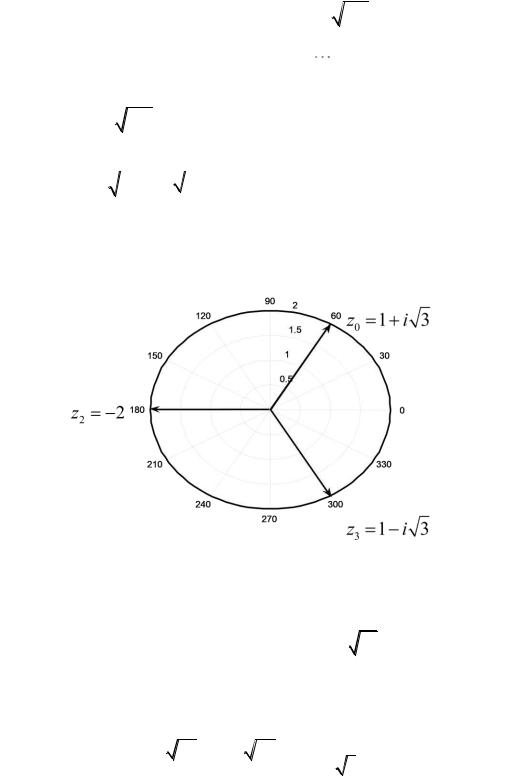
не меняет значений синуса и косинуса. Например, |
|
|||
|
225 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
cos n k . |
|
cos k |
cos |
|
|
( k) 2 |
cos |
|
|
(n k) |
||
n |
n |
|||||||||
|
n |
|
|
n |
|
|
|
Итак, мы получили n корней n -й степени из комплексного числа. Это –
комплексные числа, модули которых равны |
r n | a | , а аргументы опреде- |
|||||
ляются формулой |
|
|
2 |
k, |
k 0, 1, |
2, , n 1. Особенно наглядна |
|
|
|||||
|
n |
|
n |
|
|
|
их геометрическая интерпретация: все корни расположены на окружности,
|
|
|
2 |
. |
|
радиус которой r n | a | , и угол между соседними корнями равен |
|||||
|
|||||
|
|
|
n |
||
Например, уравнение z3 8 0 имеет три корня, расположенных на окруж-
|
|
|
|
|
|
|
||
ности радиуса r 3 | 8 | 3 |
8 2 . |
Поскольку arg( 8) , то аргументы |
||||||
корней соответственно равны |
|
k |
|
|
2 |
k , k 0, 1, 2 . |
||
|
3 |
3 |
||||||
|
|
|
|
|
|
|
||
Рис. 32.1 |
|
В области действительных чисел символ |
( ) был «закреплён» за |
положительным корнем из положительного числа. Если расширить его применение для изображения корня из комплексного числа, то он потеряет однозначность. Например,
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 i , 3 8 |
|
|
|
. |
|||
|
|
||||||
|
|
|
1 |
i |
3 |
|
|
|
|
|
|
|
|
|
|
226
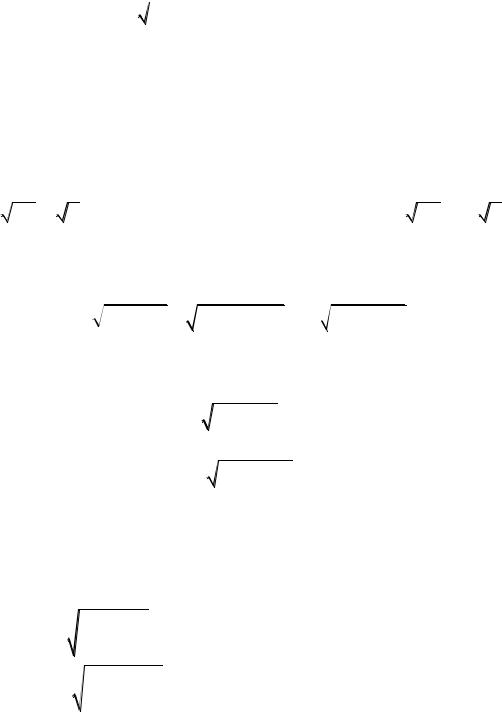
32.2.Квадратное уравнение.Рассмотрим квадратное уравнение
ax2 bx c 0 , коэффициенты которого действительные числа. Формально написанная формула для вычисления его корней
x |
b |
|
b2 4ac |
(32.1) |
|
|
|
||
1,2 |
|
2a |
|
|
|
|
|
||
во множестве действительных чисел не имеет смысла, если подкоренное вы-
ражение b2 |
4ac отрицательно. Но теперь мы умеем находить квадрат- |
||||||||||
ные корни из отрицательных чисел. |
Пусть d , |
(d 0) некоторое отрица- |
|||||||||
тельное число. |
Его тригонометрическая форма d d (cos i sin ) . По- |
||||||||||
этому |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(cos( k) i sin( k)), |
|
|
|
|
|
|
|
d |
d |
k 0,1 |
d i d |
|||||||
|
|
|
2 |
2 |
|
|
|
|
|
||
Следовательно, если дискриминант уравнения отрицателен, то

 b2 4ac
b2 4ac 
 (4ac b2 ) i
(4ac b2 ) i 
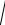 | b2 4ac | .
| b2 4ac | .
Формула вычисления корней квадратного уравнения принимает вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
b2 4ac |
, |
|
b2 4ac 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x1,2 |
|
|
|
|
|
|
|
|
2a |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
b i | b2 4ac | |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
b2 4ac 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В случае приведённого квадратного уравнения x2 px q 0 фор- |
|||||||||||||||||||||||||||
мулы имеют более компактный вид |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
p |
|
2 |
q, |
|
p |
|
|
|
2 |
q 0 |
|
|
|
||||||||
|
|
|
|
( |
|
|
) |
|
( |
|
) |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x1,2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(32.2) |
|
|
p |
|
|
|
|
p |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|||||
|
|
|
i |
| ( |
) |
2 |
q | , ( |
|
) |
2 |
q 0 |
|
|
|
|||||||||||||
|
|
2 |
2 |
|
|
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример.Решитьуравнение z3 8 0 . После разложения левой части уравнения на множители
(x 2)(x2 2x 4) 0
227

становится очевидным действительный корень уравнения x1 2 , а два комплексно сопряжённых корня находятся по формуле (32.2)
x2,3 1 
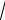 1 4 1
1 4 1 
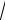 3 1 i
3 1 i
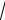 3 .
3 .
Геометрическая интерпретация корней данного уравнения дана на рис. 32.1.
32.3.Разложение многочлена на множители.Рассмотрим многочлен степени n
P (z) a zn a zn 1 |
|
a |
z a . |
||
n |
0 |
1 |
|
n 1 |
n |
Число z1 , обращающее этот многочлен в нуль ( Pn (z1 ) 0 ), называют корнем уравнения Pn (z) 0 .На протяжении многих веков делались попытки получить формулы для вычисления корней уравнений Pn (z) 0 степени
n 3. В 1545 г. итальянский математик, философ и врач Д. Кардано (15011576) опубликовал формулы решения кубического уравнения. Возник спор о приоритете с другим итальянским математиком Николло Тарталья (14991557). Ученик Кардано Л.Феррари (1522-1565) нашёл способ решения уравнений четвёртой степенипутём сведения к решению кубического уравнения. Норвежский математик Нильс Абель (1802-1829) доказал, что алгебраические уравнения степени n 4 неразрешимы в радикалах. Это надо понимать в том смысле, что корни уравненияне выражаются через его коэффициенты ak с помощью конечного числаопераций сложения, вычитания,
умножения, деления и извлечения корня.
Важный результат о существовании корней алгебраического уравнения носит название основной теоремыалгебры. Эта теорема гласит, что
всякий многочлен Pn (z) степени n 1имеет по крайнейодин комплекс-
ный корень.Эта теорема впервые (не вполне строго) была доказана французским учёным Ж. Даламбером (1717-1783).Строгое доказательство дал Карл Гаусс (1777-1855) в 1799 году. Основная теорема алгебры даёт возможность представления многочлена в виде произведения множителей, содержащих его корни
Pn (z) a0 (z z1 )(z z2 ) |
(z zn ) , |
откуда следует, что всякое алгебраическое уравнение имеет ровно n корней.
Некоторые из корней могут совпадать. Их называют кратнымив отличие от простых, т.е. неповторяющихся корней. Кратность корня – это число его повторений в разложении многочлена на множители. С учётом кратности корней получим разложение многочлена
P (z) a (z z )r1 |
(z z |
2 |
)r2 |
(z z |
k |
)rk , |
||
n |
0 |
1 |
|
|
|
|
||
|
|
228 |
|
|
|
|
|
|

где z1, , zk – различные корни уравнения Pn (z) 0 , а r1, , rk – их кратности, причём r1 rk n . Указанные разложения справедливы для многочле-
нов, как с вещественными, так и с комплексными коэффициентами. Отметим без доказательства, что если многочлен имеет вещественные
коэффициенты, то наряду с комплексным корнем z i многочлен обладает сопряжённым корнем z i , причём той же кратности. Объединяя в разложении многочлена такие пары, получаем
(z z)(z z ) (z i )(z i ) z2 2 z 2 2 z2 pz q .
Таким образом, многочлен с вещественными коэффициентами раскладывается на линейные множители с вещественными корнями и квадратичные множители с парой комплексно сопряжённых корней. Переменную в случае многочлена с вещественными коэффициентами будем обозначать буквой x . Итак, многочлен с вещественными коэффициентами имеет раз-
ложение |
|
|
|
|
|
|
|
P (x) a (x x )r1 |
(x x )rr (x2 |
p x q )s1 |
(x2 p x q )sl , |
||||
n |
0 |
1 |
k |
1 |
1 |
l |
l |
где r1 |
rk 2(s1 |
sl ) n . |
|
|
|
|
|
32.4. Разложение правильных дробей на простые дроби.Разложение многочлена на множители связано с задачей разложения правильной рациональной дроби
|
|
|
Qm (z) |
|
|
(32.3) |
|
|
|
|
Pn (z) |
|
|||
|
|
|
|
|
|||
на простые дроби следующих видов; |
|
|
|||||
|
A |
и |
|
Mx N |
( k |
1 и целое); |
|
|
|
|
|
||||
|
(x a)k |
|
(x2 px q)k |
||||
|
|
|
|
|
|
||
где A, M , N, a, p, q – |
действительные числа, а квадратный трёхчлен |
||||||
x2 px q не имеет действительных корней. Оказывается, что всякую
правильную рациональную дробь можно представить в виде суммы конечного числа простейших дробей. Этот алгебраический факт мы примем без доказательства.
Рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе ( m n ). В противном случае ( m n ) рациональная дробь называется неправильной. Всякую неправильную рациональную дробьможно
229
