10298

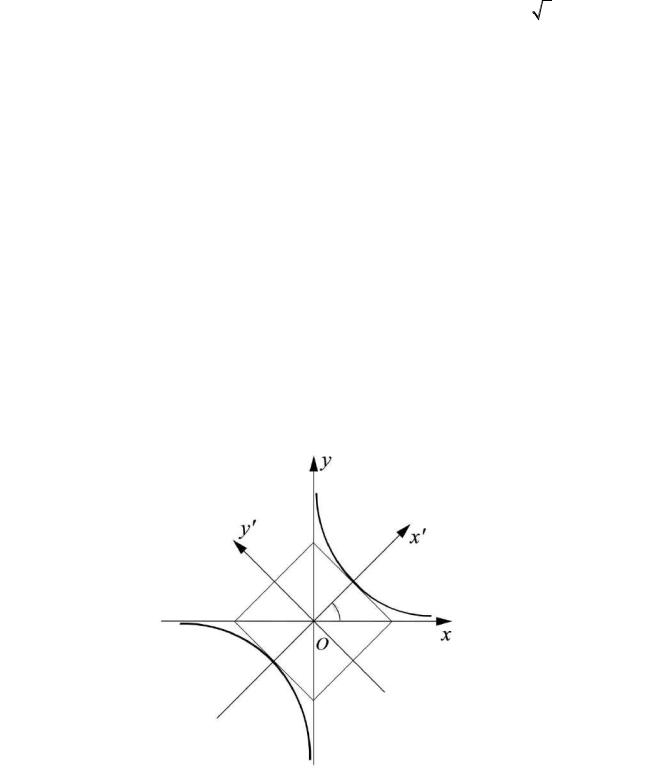
Рис. 26.7

Для приведения уравнения xy 3 к каноническому виду рассмотрим по-

проделав соответствующие преобразования, получим в новой системе коор-

асимптотами являются исходные оси координат O x и Oy (рис. 26.8).

Итак, преобразования поворота и (или) параллельного переноса осей координат используются для того, чтобы уравнение (26.2) в новой системе координат приобрело канонический вид. Проанализируем возникающие ситуации. Для этого рассмотрим коэффициенты A и C при квадратах переменных в канонических уравнениях основных линий и найдём их произведение. Для

AC 0 . Остальные виды канонических уравнений можно распределить по типам таким образом, чтобы для каждого из уравнений первого типа число AC было положительно, отрицательно для второго и равно нулю для уравнений третьего типа.

Рис. 26.8

Тогда получаем классификацию:

I. Эллиптический тип

190

III. Параболический тип

6)y2 = 2 px (парабола),

7)y2 = a2 (пара параллельных прямых),

8)y2 = 0 (прямая),

9)y2 = - a2 (пустое множество).

Полученную классификацию можно использовать в любой задаче, связанной с уравнением второго порядка – даже если, например, в нём B 0 . Оказывается, по исходным коэффициентам уравнения (26.2), которые присутствуют в конкретной задаче, можно сразу определить, к какому типу от-

Итак, мы проделали необходимую работу, чтобы полностью разобраться с построением линий во всех ситуациях, к которым приводит уравнение второго порядка (26.2). Сначала определяем тип линии, задаваемой уравнением. Далее приводим его к каноническому виду, выполняя рассмотренные преобразования координат.

191

Лекция 27. Поверхности второго порядка

Переходим к изучению поверхностей в трехмерном пространстве. Будем рассматривать поверхности, задаваемые уравнениями, включающими вторые степени текущих координат x , y и z или их взаимное произведение.

Уравнение вида

Ax2 By2 Cz2 2Dxy 2Exz 2Fyz 2Gx 2Hy 2Kz L 0 , (27.1)

где коэффициенты A, B,C, D, E ,F ,G , H , K иL — любые действительные числа, но, по крайней мере, одно из чисел A, B или C отлично от нуля (т.е.

A2 B2 C2 0 ), называется общим уравнением поверхности второго

порядка.

Также как и для кривых второго порядка, для поверхностей второго порядка существует полная классификация. С помощью подходящего параллельного переноса и поворота осей координат (теперь уже выполняемых в пространстве) любое уравнение второго порядка может быть приведено к одному из семнадцати видов. Этим уравнениям в пространстве отвечают

192

классические поверхности: эллипсоид, однополостный и двуполостный гиперболоиды, конус, эллиптический и гиперболический параболоиды, а также целая группа поверхностей, называемых цилиндрическими.

27.1. Цилиндрические поверхности. Поверхность, состоящая из па-

раллельных прямых (так называемых образующих), проходящих через каждую точку заданной линии L (направляющей), называется цилиндрической поверхностью. Образно можно представить, что цилиндрические поверхности образуются движением прямой, которая перемещается в пространстве вдоль кривой L , сохраняя постоянное направление (рис. 27.1).

В качестве направляющей цилиндрической поверхности рассмотримрасположенную в плоскости xOy линию L , которая задаётся уравнением

F(x, y) 0 . Пусть M0 (x0 , y0 ,0) – произвольная точка направляющей (рис. 27.1). Тогда F (x0 , y0 ) 0 . Если рассматривать цилиндрическую поверх-

ность, образующие которой параллельны координатной оси Oz , то уравнение образующей, проходящей через точку M0 (x0 , y0 ,0) ,примет вид

y y0

Рассмотрим произвольную точку M (x0 , y0 , z0 ) этой образующей. Её координаты удовлетворяют уравнению F (x, y) 0 при любом значении переменной z . Точка M0 (x0 , y0 ,0) выбиралась произвольно, поэтому можно

утверждать, что координаты всех точек цилиндрической поверхностиудовлетворяют уравнению F (x, y) 0 .

Рис. 27.1

193

Ясно, что уравнение вида F (x, z) 0 задаёт цилиндрическую поверхность с образующими, параллельными оси Oy , а уравнение вида F ( y, z) 0

задаёт цилиндрическую поверхность с образующими, параллельными оси

O x .

Рис. 27.2

Если направляющей цилиндрической поверхности является кривая второго порядка, то поверхность называется цилиндрической поверхностью второго порядка (или цилиндром второго порядка). В зависимости от конкретного вида уравнения получаются различные типы цилиндров второго порядка. Их названия соответствуют названиям направляющих линий L .

Например, уравнение x2 y2 1 задаёт в пространстве цилиндриче- a2 b2

скую поверхность с образующими, параллельными оси Oz .Его направляющей является эллипс, а поверхность, задаваемая этим уравнением, называется эллиптическим цилиндром (рис. 27.2). Частным случаем эллиптического цилиндра является круговой цилиндр. Его уравнение в канониче-

ском виде имеет вид x2 + y2 = R2 .

Уравнение вида x2 2 py определяет в пространстве параболиче-

ский цилиндр (рис. 27.3).

194

Рис. 27.3

27.2. Поверхности вращения образуются вращением какой-либо плоской линии L (образующей) вокруг прямой (оси поверхности враще-

ния), расположенной в плоскости этой линии. Примером служит сфера: её можно рассмотреть как поверхность, образованную вращением полуокружности вокруг её диаметра. Покажем, как можно получить уравнение поверхности вращения, исходя из уравнения образующей (лежащей в одной из координатных плоскостей) и уравнения оси вращения (совпадающей с одной из координатных осей, расположенных в той же плоскости).

Будем вращать расположенный в плоскости yOz эллипс с уравнением

y2 z2 1 вокруг координатной оси Oz . Полученную поверхность рассе- b2 c2

чём плоскостью, параллельной координатной плоскости xOy и проходящей через фиксированную точку O (0, 0, z) (рис. 27.4).

Рис. 27.4

195

Пусть M (x, y, z) – произвольная точка поверхности вращения, лежащая в плоскости сечения. Рассмотрим в плоскости yOz точку поверхности M (0, y , z) . Еёордината по абсолютной величине равна радиусу окружности, на которой лежит точка M (x, y, z) , т.е. O M O M , поэтому x2 y2 y 2 . Находящаяся в плоскости yOz точка M (0, y , z) принадлежит и плоскости сечения, и исходному эллипсу. Это означает, что её координаты

Рис. 27.5

От этих примеров нетрудно перейти к алгоритму получения уравнения поверхности вращения по уравнению исходной кривой, если осью вращения служит одна из координатных осей. В уравнении кривой слагаемое с переменной, наименование которой совпадает с наименованием оси вращения, останется без изменения, а квадрат другой переменной заменяется на сумму квадратов этой переменной и переменной, отсутствовавшей в уравнении.

196

Лекция 28. Канонические уравнения поверхностей второго порядка

Теперь перейдем к другим поверхностям второго порядка, определяемым общим уравнением

Ax2 By2 Cz2 2Dxy 2Exz 2Fyz 2Gx 2Hy 2Kz L 0.

Каждая поверхность может быть построена по её уравнению методом сечений. Проследим, как образуются поверхности второго порядка, проявляясь постепенно по мерестыковки разных сечений.

Уравнение сечения этой поверхности координатной плоскостью xOz полу-

виду уравнения мы узнаём эллипс и можем изобразить его в соответствующей плоскости (рис. 28.1).

197

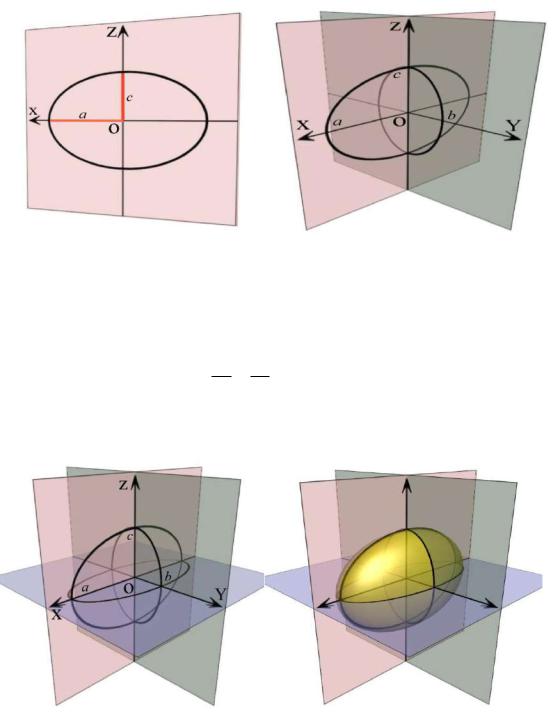
Рис. 28.1

При x 0 из (28.1) получаем уравнение другого эллипса, располагающегося в плоскости yOz и имеющего те же точки пересечения с осью

Oz , что и первый эллипс: y2 z2 1. Рисунок дополняется эллипсом в b2 c2

плоскости xOy (рис. 28.2).

Рис. 28.2

Рассмотрим произвольную плоскость z h (где h – любое число), параллельную xOy . Сечение исходной поверхности (28.1) этой плоскостью

задаётся уравнением

То есть при всех h c в сечении эллипсоида(28.1) плоскостями z h полу-

ah a , bh b . При уменьшении h полуоси ah и bh увеличиваются, достигая наибольших значений ah a и bh b ,если h 0 . Таким образом, «самый крупный» эллипс образуется в сечении координатной плоскостью xOy . Аналогичная картина получается в сечениях поверхности (28.1) плоскостями, параллельными координатным плоскостям xOz и yOz .

Отметим, что на плоскости нет точек, отвечающих условию z c . Т.е. у поверхности, которую мы строим, нет пересечения с плоскостями z h

нении при этом получается a2 b2 0 . Общий вид поверхности отражаем

рисунком 28.2. Вполне естественно, что эта поверхность носит название «эллипсоид» – по названиям сечений.

Эллипсоид обладает тремя взаимно перпендикулярными плоскостями симметрии (при данном выборе осей они совпадают с координатными плоскостями). Величины a , b и c называются полуосями эллипсоида. Если две из трёх полуосей одинаковы, то, эллипсоид становится эллипсоидом вращения. Если a b c , то уравнение (28.1) определяет сферу.

28.2. Гиперболоиды. Рассмотрим уравнение однополостного гипер-

болоида

В сечениях координатными плоскостями xOz и yOz поверхности, опреде-

ляемой этим уравнением, получаются гиперболы, а в сечениях, параллельных координатной плоскости xOу – эллипсы. В целом поверхность выгля-

дит, как бесконечная трубка, расширяющаяся в обе стороны от горлового эллипса (рис. 28.3).

199