
7535
.pdf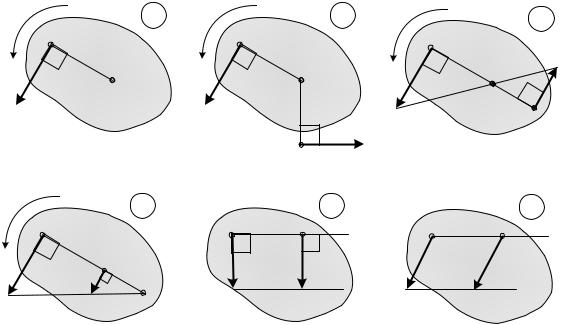
50
На найденном направлении отложить отрезок AР равный de 5f и ∙ T
получить положение точки Р, которая является мгновенным центром скоростей.
2) Известны направления скоростей двух точек плоской фигуры |
|
и |
g |
|||||
и эти скорости не параллельны друг другу (рис. 2.15 б). |
|
|
||||||
Для определения МЦС надо из точек А и В восстановить перпендикуляры |
||||||||
к направлению скоростей до точки их пересечения |
P, |
которая и будет точкой |
||||||
МЦС. |
|5fb| |gb5h | L. |
|
|
|
|
|
|
|
При этом |
|
|
g |
|
|
|
|
|
3) Cкорости двух точек плоской фигуры |
и |
параллельны друг дру- |
||||||
гу и перпендикулярны отрезку АВ. |
|
|
|
|
|
|||
МЦС находится из условия, что модули скоростей точек А и В пропорцио-
нальны5 расстояниям5 от этих точек до МЦС:
| f | | h | Lb gb .
Возможны два варианта:
∙МЦС находится между точками А и В, когда скорости направлены в разные стороны (рис. 2.15 в);
∙МЦС находится за пределами отрезка АВ, когда скорости не равны и направлены в одну сторону (рис. 2.15 г).
A |
|
A |
ω |
P |
ω |
R |
|
R |
vA |
|
vA |
|
A |
A |
|
|
|
ω |
B |
R |
|
|
vA |
|
|
P |
R |
R |
|
vA |
vB |
ω = 0 |
|
|
|
|
A |
|
|
R |
|
|
vB |
P |
ω |
P |
|
|
R |
|
R |
vA |
|
vB |
|
B
B |
A |
B |
||
R |
R |
R |
||
vB |
vA |
|||
v |
B |
|||
ω = 0
Рис. 2.15 |
|
||
4) Cкорости двух точек плоской фигуры |
и |
g равны по модулю и па- |
|
раллельны друг другу. При этом они могут |
быть перпендикулярны или непер- |
||
|
|
|
|
51
пендикулярны отрезку АВ (рис. 2.15 д,е).МЦС в этом случае располагается в бесконечности. Скорости всех точек тела одинаковы.
L 0 |
|
ω |
|
Движение тела является мгновенно поступательным и |
|
|
|
|
. |
|
|
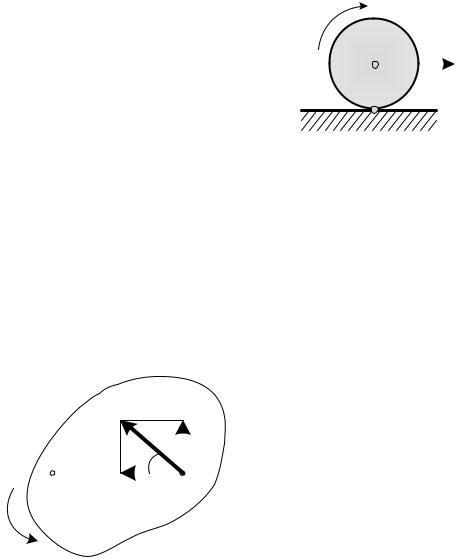
5) При качении тела по неподвижной поверхности |
O |
|
|
скорости соприкасающихся точек равны в том случае, |
|
R |
|
|
vO |
||
P
если отсутствует проскальзывание между телами (рис. 2.16). МЦС находится в точке соприкосновения тела с поверхностью.
Рис. 2.16
2.3.9 Теорема о сложении ускорений
Ускорение точки плоской фигуры равно векторной сумме ускорения по-
люса и ускорения, которое имеет эта точка в относительном вращении фигуры |
||||||
вокруг полюса: |
4a 4` ( 4a`. |
|
|
|
|
|
|
|
|
a MC |
aτMC |
||
|
|
|
R |
R |
||
|
ε |
|
β |
|
M |
|
|
|
|
||||
|
|
|
|
|
||
|
|
Rn |
|
|||
|
C |
|
|
|||
|
a MC |
|
|
|||
|
|
|
|
|
||
Рис. 2.17
Ускорение 4a` определяется по правилам вращательного движения, то
есть равно сумме вращательного и центростремительного ускорений:
4a` 4a`/ ( 4a`.
Тогда полное ускорение точки М будет равно:
4a 4` ( 4a`/ ( 4a`.

52
ГЛАВА 3. ДИНАМИКА
3.1 Предмет и задачи динамики
Динамикой называется раздел механики, в котором изучается движение механических систем под действием сил.
Динамика является синтезом двух предыдущих разделов теоретической механики:
∙статики, которая изучает преобразования систем сил и условия их равновесия, и
∙кинематики, которая изучает способы математического описания движения тел.
Основной закон динамики
Фундаментальное значение имеет второй закон Ньютона, который называют основным законом динамики:
Сила, действующая на свободную материальную точку, сообщает ей ускорение, которое в инерциальной системе отсчета пропорционально этой силе:
R = m a F
В уравнение входит величина m, которая называется массой материальной точки. Она является мерой инертности точки: чем больше масса, тем меньшее ускорение сообщает точке приложенная сила
Масса измеряется в килограммах (кг), и, следовательно, единица силы
(ньютон) будет равна 1 Н = 1 кг× м .
с2
Примечания:
∙Если на точку действует несколько сил, то под R в уравнении следует
F
понимать их равнодействующую:
R |
n R |
|
m a |
= ∑ Fi |
. |
|
i=1 |
|
∙Если точка не является свободной, то нужно воспользоваться принципом |
||
освобождаемости |
от связей и к действующим на точку силам добавить соот- |
|
ветствующие реакции.
3.2 Динамика материальной точки
Задачи, решаемые методами динамики, условно можно разделить на две группы:
53
∙Первая задача динамики (прямая) предполагает, что закон движения механической системы известен, а силы которые вызывают это движение необходимо найти.
∙Вторая задача динамики (обратная) предполагает, что известны силы, действующие на механическую систему, а найти необходимо закон движения.
3.2.1 Дифференциальные уравнения движения материальной точки
Пусть материальная точка движется в инерциальной системе отсчета. Если движение задано в векторной форме, то
|
|
|
|
R |
||
R |
= |
d 2 r |
||||
a |
|
, |
||||
dt 2 |
||||||
и тогда основной закон динамики примет вид, который называют диффе- |
||||||
ренциальное уравнение движения материальной точки в векторной форме. |
||||||
|
|
2 R |
|
R |
||
|
|
d r |
|
|||
m |
= F |
|||||
dt 2 |
||||||
|
|
, |
||||
в котором сила может зависеть от положения точки, от скорости точки и от |
||||||
времени, то есть: |
|
|
|
|
|
|
R |
|
|
R |
R R |
||
F |
|
= F |
(r , v, t ). |
|||
Спроектировав векторное равенство на оси, получим дифференциальные уравнения движения материальной точки в координатной (аналитической) форме:
.
Дифференциальные уравнения движения материальной точки в естественных осях могут быть получены с помощью формул кинематики, после чего они приобретают следующий вид:
m |
dvτ |
= F |
||||
|
|
|
||||
|
|
dt |
τ |
|||
|
|
|
||||
|
|
v |
2 |
|
|
|
m |
|
|
= F |
|||
ρ |
||||||
|
|
n |
||||
|
|
|
|
|
. |
|
3.2.2 Первая задача динамики
Если закон движения задан в векторной форме, выражение для вектора силы могут быть найдены путем дифференцирования радиус-вектора.
Если закон движения задан в аналитической форме, проекции силы на декартовые оси могут быть найдены путем дифференцирования координат.

54
Если закон движения задан в естественной форме, проекции силы на естественные оси быть найдены путем дифференцирования дуговой координаты.
3.2.3 Вторая задача динамики
Вторая задача динамики заключается в определении движения под действием заданных сил. Ее решение сводится к интегрированию дифференциальных уравнений.
Пусть, движение точки в плоскости описывается в декартовых осях. Тогда
система уравнений: = 7 %, , , = 7 &, , ,
имеет общее решение в виде:
x = x (t, C , C |
, D , D |
) |
|
|||
|
1 |
2 |
1 |
2 |
) |
|
y = y (t, C , C , D , D |
. |
|||||
|
1 |
2 |
1 |
2 |
|
|
|
|
|
||||
При решении задач обычно принимают, что t0 = 0 , а С1, С2, D1, D2 − посто-
янные интегрирования, которые определяются из начальных условий, описывающих состояние материальной точки в начальный момент времени.
В качестве начальных условий задаются начальное положение точки и ее начальная скорость:
x0y0x&0
y&0
=x
=y
=x&
=y&
t =0
t =0
t =0
t =0
Из этих уравнений определяются четыре постоянные интегрирования.
3.2.4 Интегрирование уравнения прямолинейного движения
Пусть материальная точка движется в положительном направлении оси x .
Тогда |
a |
|
= |
dvx |
= |
dv |
, |
F = F . |
x |
|
|
||||||
|
|
|
dt dt |
|
x |
|||
|
|
|
|
|
|
|||
Запишем дифференциальное уравнение движения
mdv = F (x, v,t ) dt
ирассмотрим способы его интегрирования с учетом начальных условий
x0 = x=x&0 x&
t =0
t =0
для трех частных случаев:
∙когда сила зависит от времени F = F (t ),

55
∙когда сила зависит от скорости F = F (v),
∙когда сила зависит от координаты F = F (x).
Частный случай 1: сила зависит от времени: m dv = F (t ).
dt
Умножив обе части уравнения на dt , разделим переменные t и v : m dv = F (t )dt
При интегрировании уравнения можно пользоваться определенными или неопределенными интегралами.
Интегрируем левую и правую части.
m ∫dv = ∫F (t )dt , откуда mv = ∫F (t )dt +C1 ,
где C1 определяется из начального условия.
Частный случай 2: сила зависит от скорости: m dv = F (v).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||
Умножив обе части равенства на |
|
, |
получим |
|||||||||||||||||||||
F (v) |
||||||||||||||||||||||||
m |
|
dv |
= dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
F (v) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Интегрируем левую и правую части. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
m ∫ |
dv |
|
|
= ∫dt , откуда |
m∫ |
|
dv |
=t +C1 , |
||||||||||||||||
F (v) |
F (v) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где C1 определяется из начального условия. |
|
|
|
|
|
|||||||||||||||||||
Частный случай 3: |
сила зависит от координаты: m |
dv |
= F (x). |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
||||
Выполним замену |
|
dv |
= |
dv |
× |
dx |
= |
dv |
v , получим уравнение mv |
dv |
= F (x). |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
dt dx dt |
|
dx |
|
|
|
|
|
|
|
|
dx |
|||||||||
Умножим обе части уравнения на dx : |
|
|
|
|
|
|
|
|
||||||||||||||||
mvdv = F (x)dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Интегрируем левую и правую части. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
m∫vdv = ∫F (x)dx , |
откуда |
m |
v2 |
= |
∫F (x)dx + C1 . |
|||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
Постоянная C1 определяется из начального условия.
Если требуется получить не только выражение скорости v(t ), но и выра-
жение для координаты точки x(t ), то процесс интегрирования надо повторить.
56
3.3Динамика материального тела
3.3.1Классификация сил. Основные теоремы динамики
Рассмотрим механическую систему, состоящую из n точек. Положение k-й
R
точки определяется радиус-вектором rk . Точка имеет массу mk и движется со
R R
скоростью vk и с ускорением ak .
Силы, действующие на материальную точку можно разбить на две группы. Сделать это можно разными способами.
Первый способ
Разделим силы, действующие на k-ю точку, на внешние и внутренние. Получим следующую запись основного уравнения динамики:
|
R |
(k = 1, 2,..., n) |
|
ma = Fke + Fki |
|
где |
Fke (external ) − равнодействующая внешних сил, |
|
Fki |
(internal ) − равнодействующая сил, действующих со стороны тел си- |
|
стемы.
Второй способ
Разделим силы, действующие на k-ю точку, на активные силы и реакции связей. Получим следующую запись:
|
R |
(k = 1, 2,..., n) |
|
|
ma = Fk + Rk |
||
где |
Fk − равнодействующая активных сил, приложенных к точке k , |
||
Rk − равнодействующая реакций связей, действующих на точку k. |
|||
При этом выполнится равенство |
Fe + Fi = F + R . |
||
|
|
|
k k k k |
Первый способ записи основного уравнения используется при решении задач динамики с помощью основных теорем динамики, которые включают в себя:
∙теорему о движении центра масс, ∙теорему об изменении количества движения,
∙теорему об изменении кинетического момента, ∙теоремы об изменении кинетической энергии.
57
3.3.2 Теорема о движении центра масс
Центр масс механической системы
Массой механической системы называется сумма масс ее точек:
|
n |
|
|
m = ∑ mk |
|
||
|
k =1 . |
|
|
Центром масс механической системы называется геометрическая точка С, |
|||
радиус-вектор которой определяется по формуле: |
|||
R |
1 n |
R |
|
rC = |
|
∑ mk rk |
|
|
|||
|
m k =1 |
|
|
Проектируя последнее равенство на оси, получим формулы для координат центра масс, которые аналогичны формулам для определения координат центра тяжести:
|
|
1 |
|
n |
|
|
xC |
= |
|
∑ mk xk |
|
||
|
|
, |
||||
|
|
m k =1 |
||||
|
|
|
1 |
|
n |
|
yC |
= |
|
∑ mk yk |
|
||
|
|
. |
||||
|
|
|
m k =1 |
|||
Центр масс более общее понятие, чем центр тяжести, поскольку сохраняет смысл даже при отсутствии сил тяжести.
Дифференцированием получим выражение для скорости центра масс
R |
|
1 |
n |
R |
vC |
= |
|
∑ mk vk |
|
|
||||
|
|
m k =1 |
, |
|
и выражение для ускорения центра масс системы:
R |
|
1 |
n |
R |
aC |
= |
|
∑ mk ak |
|
|
||||
|
|
m k =1 |
|
|
Теорема о движении центра масс механической системы
Произведение массы системы на ускорение центра масс равно главному вектору внешних сил, действующих на точки системы:
R |
n |
R |
|
|
|
maC = ∑ Fke |
||
|
k =1 |
|
или в проекциях на оси |
||
&& |
= |
n |
e |
||
mxC |
∑ Fkx |
|
|
|
k =1 |
|
|
n |
&& |
= |
e |
myC |
∑ Fky |
|
|
|
k =1 |
То есть, центр масс механической системы движется как материальная точка, в которой сосредоточена вся масса системы и к которой приложены все

58
внешние силы, действующие на систему. При этом внутренние силы не могут изменить движение центра масс.
Сохранение движения центра масс
Следствие 1
Если главный вектор внешних сил механической системы все время равен
n R |
|
|
|
|
нулю ∑Fke = 0 |
, то центр масс системы находится в покое или движется равно- |
|||
k =1 |
R |
|
R |
|
|
= const |
= 0 ). |
||
мерно и прямолинейно vC |
( aC |
|||
Следствие 2
Если сумма проекций всех внешних сил на какую-либо ось все время равна
n
нулю ∑Fkxe = 0 , то проекция скорости центра масс на эту ось постояннаvCx = const
k =1
( &&xC = 0 ). Центр масс движется по оси х равномерно или покоится.
3.3.3 Теорема об изменении количества движения
Количеством движения материальной точки называется векторная вели-
чина, равная произведению массы точки на ее скорость: |
R |
||||
Q = mv . |
|||||
Количеством движения материальной системы называется векторная сум- |
|||||
|
|
|
R n |
R |
|
ма количеств движения всех точек системы: Q = ∑mr vr . |
|||||
|
|
|
r =1 |
|
|
n |
R |
R |
R |
|
|
|
|
|
|||
Поскольку ∑mk vk |
= mvC , то |
Q = mvC . |
|
|
|
k =1
Количество движения характеризует только поступательную часть движения и никакого отношения не имеет к его вращательной составляющей.
Теорема об изменении количества движения в дифференциальной форме
Производная по времени от количества движения механической системы равна главному вектору внешних сил, действующих на систему:
dQ = ∑n R e Fk
dt k =1
или в проекциях на оси:
dQ |
n |
||
|
|
x |
= ∑Fkxe |
|
|
||
dt |
|
k =1 |
|
|
|
|
|
dQ n
y = ∑Fkye
dt k =1

59
Теорема об изменении количества движения системы может применяться для систем, имеющих переменную массу, в то время как теорема о движении центра масс системы справедлива только для систем с постоянной массой.
Теорема об изменении количества движения в интегральной форме Импульсом силы за некоторый промежуток времени (0,t ) называется ве-
личина равная интегралу от силы по времени
R |
t R |
S |
= ∫F dt |
|
0 |
Если F = const, |
то естественно, что S = F ×Dt , где t − промежуток времени. |
Размерность импульса силы [S ]= Н × с = кг × м совпадает с размерностью ко-
с
личества движения.
Теорема:
Изменение количества движения механической системы за некоторый промежуток времени равно сумме импульсов действующих на систему внеш-
|
|
|
|
R n |
R |
них сил за этот промежуток времени: |
DQ = ∑Ske |
||||
|
|
|
|
k =1 |
|
или в проекциях на координатные оси |
|
||||
|
|
e |
|
|
|
|
|
n |
|
|
|
|
Qx |
= ∑Skx |
|
|
|
|
|
k =1 |
. |
|
|
|
|
n |
|
|
|
|
Qy |
e |
|
|
|
|
= ∑Sky |
|
|
|
|
|
|
k =1 |
|
|
|
Для одной материальной точки теорема приобретает вид: = W = i,
где i - импульс равнодействующей всех сил, приложенных к точке. Отсюда видно, что импульс является характеристикой силы, показываю-
щей насколько эта сила изменяет количество движения материальной точки или механической системы. Внутренние силы не могут изменить количество движения механической системы.
Сохранение количества движения
Следствие 1
Если главный вектор внешних сил механической системы все время равен
|
n R |
|
|
R |
нулю ∑Fi e |
º 0 |
, |
то вектор количества движения системы постоянен Q º const , |
|
|
i=1 |
|
|
|
R |
≡ const . |
|
|
|
mvC |
|
|
|
|
