
7535
.pdf
40
окресностях рассматриваемой точки. Радиус этой9 1окружности⁄; назовем радиусом кривизны траектории в данной точке: .
Радиус кривизны измеряется в метрах.
Обратная величина называется кривизной данной кривой в точке М:
8<=> → |>@-|=k.
Примеры:
1)Окружность является кривой постоянной кривизны. Во всех точках окружности радиус ее кривизны равен радиусу окружности.
2)Прямая линия является линией постоянной кривизны. Во всех ее точках радиус кривизны равен бесконечности, а кривизна равна нулю.
3)У таких линий, как эллипс или парабола, радиус кривизны в разных точках имеет разное значение.
Естественные оси
Рассмотрим точку М, которая двигается по произвольной траектории. Проведем через точку М касательную к траектории. Перпендикулярно к касательной проведем ось, которая называется нормаль (рис. 2.6). Касательная и нормаль вместе образуют естественные оси.
"−" |
R |
"+" |
|
n |
|
|
90° |
τR |
|
M |
|
Рис. 2.6 |
|
|
|
|
Естественные оси являются подвижными, они перемещаются по траектории. С естественными осями связаны единичные векторы (орты):
τ – единичный вектор касательной; n – единичный вектор нормали.
Единичный вектор касательной всегда направлен в положительныю сторону дуговой координаты, а единичный вектор нормали всегда направлен в сторону вогнутости траектории.
2.2.5 Определение ускорения при естественной форме задания движения
Можно показать4 , 4что(ускорение4 4 . (равно4 * векторной сумме:
/ / .
41
Касательное ускорение |
|
направлено по касательной к траектории и |
||||||
определяется проекцией вектора4ускорения/ |
на касательную, знак которой пока- |
|||||||
зывает в какую сторону дуговой координаты s оно направлено: |
||||||||
ния Проекцию |
4/ 5A 7 |
|
|
|
||||
4/ |
называют алгебраическим значением касательного ускоре- |
|||||||
Модуль касательного ускорения |
|4/| равен производной от модуля скоро- |
|||||||
|
| |
4 |
/| |
B B |
| |
|
|
|
сти: |
|
5 |
|. |
|
|
|||
Нормальное ускорение 4 |
направлено по главной нормали и его проек- |
|||||||
ция на нормаль всегда положительна: |
4 5C6 |
|||||||
По этой причине оно всегда направлено в сторону вогнутости траектории. |
||||||||
Модуль полного ускорения равен |
4 '4/ ( 4 . |
|||||||
2.2.6 Классификация форм движения точки
Прямолинейное движение и криволинейное движение
Траекторией точки при криволинейном движении является кривая, и ее кривизна имеет конечное значение, а радиус кривизны не равен нулю.
Траекторией при прямолинейном движении является9 ∞ прямая линия. Радиус кривизны прямой линии4 бесконечен0 . Нормальное ускоре-
ние в этом случае равно нулю . Следовательно, при прямолинейном движении полное ускорение совпадает с касательным: 4 4/ и 4 B5B.
В этом случае скорость всегда направлена по одной линии − траектории, откуда вытекает вывод о физическом смысле касательного ускорения: каса-
тельное ускорение характеризует изменение модуля скорости.
Равномерное движение и неравномерное движение
Равномерным называется такое движение точки, при котором модуль ско- |
||||
|
+,* |
4 |
B B 0 |
|
рости все время остается постоянным: |
|
. Тогда | /| |
5 |
и |
полное ускорение совпадает с нормальным: |
. |
|
|
|
|
откуда вытекает вывод о физиче- |
|||
Модуль скорости при этом не меняется,4 4 |
|
|
|
|
ском смысле нормального ускорения: нормальное ускорение характеризует
изменение направления скорости. |
E ⁄E |
+,* |
|
|
При равномерном движении |
/ |
|
. Интегрируя это равен- |
|
|
|
|||
/ ( . |
|
|
|
|
ство, получим уравнение |
равномерного движения: |
|
||
42
Это уравнение определяет величину дуговой координаты в любой момент |
||
времени. Пройденный точкой путь |
F |
определяется путем интегрирования |
модуля скорости: F G E. |
|
|
При равномерном движении F . |
|
|
Равномерное прямолинейное движение
В4этом4случае4 равны0 нулю и касательное, и нормальное, и полное ускоре- ния: а скорость/ точки как, вектор будет постоянна: +,* .
Ускоренное движение и замедленное движение
Ускоряется или замедляется движение точки можно определить по взаимному расположению векторов скорости и касательного ускорения. Если оба вектора направлены в одну сторону, то движение является ускоренным, а если в разные, − то замедленным.
При ускоренном движении произведение проекций4 1 0 этих векторов на касательную к траектории4 3будет0 положительным ( / / ), а при замедленном – отрицательным ( / / ).
Равнопеременное движение Равнопеременным называется движение точки, при котором модуль каса-
тельного ускорения все время остается постоянным: |
/ |
|
||
|
|
|||
Оно бывает равноускоренным или |
равнозамедленным. |
|||
|
4 |
+,* . |
||
Дважды интегрируя равенство |
5A 4/ +,* , |
получим выражения |
||
для скорости и дуговой координаты, то есть уравнения равнопеременного движения:
/ 4/ ( ; |
4/ 6 ( ( , |
. |
где и − начальные значения величин / и |
||
2.3 Движение твердого тела
Уравнения движения твердого тела должны позволять в любой момент времени определить положение и кинематические характеристики любой его точки.
Простейшими видами движения твердого тела являются поступательное и вращательное движения.

43
2.3.1 Поступательное движение твердого тела
Поступательным движением называется движение, при котором любой отрезок принадлежащий телу перемещается, оставаясь параллельным своему первоначальному направлению.
Все точки твердого тела, движущегося поступательно, описывают совпадающие при наложении, траектории и в каждый момент времени имеют одинаковые скорости и одинаковые ускорения.
|
B |
B |
B |
y |
|
|
|
|
|
|
|
|
|
R |
|
|
R |
rBA |
R |
R |
rBA |
|
rBA |
rB |
|
|
|
R |
|
|
|
rA |
A |
A |
A |
O |
|
|
|
|
x |
|
|
Рис. 2.7
Поступательное движение твердого тела полностью определяется движением какой-либо его точки, например центра тяжести. В этом случае имеют смысл выражения «скорость тела» или «ускорение тела». При других формах движения каждая точка тела имеет свою скорость и свое ускорение.
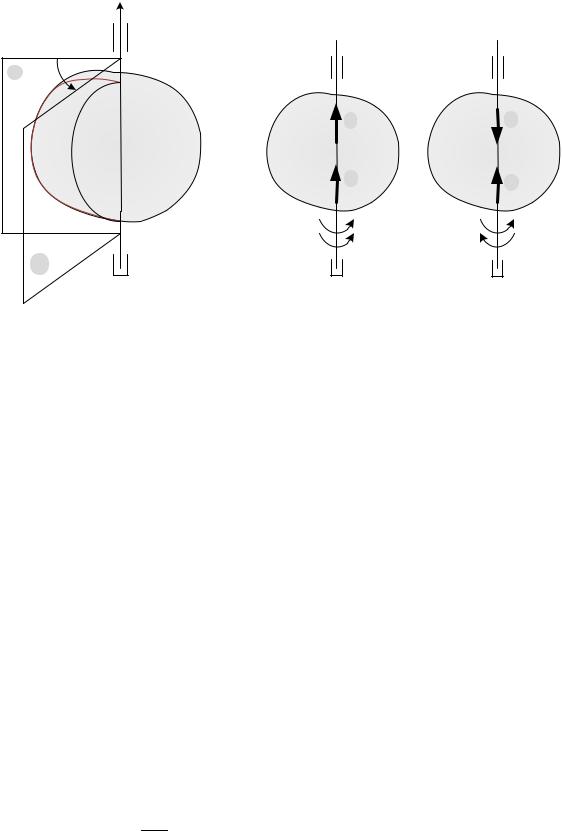
2.3.2 Вращательное движение твердого тела
Движение тела, при котором все точки тела, лежащие на некоторой прямой, остаются неподвижными, называется вращательным движением. При этом сама прямая называется осью вращения.
Точки, не лежащие на оси, при движении описывают окружности в плоскостях, которые перпендикулярны к оси вращения.
44
|
z |
Π |
ϕ |
|
Π1 |
ε |
ε |
R |
ω |
ω |
|
|
R |
ω |
ω |
ε |
ε |
Рис. 2.8
Проведем через ось вращения полуплоскость, которая в начальный момент времени занимает положениеH . В процессе вращения эта плоскость будет поворачиваться наH уголH , который меняется в зависимости от времени:
Это уравнениеH называется уравнением вращательного движения твердого тела. Знак угла положителен при отсчетеHпротив! радчасовой. стрелки.
Угол измеряется в радианах, то есть Основные кинематические характеристики такого движения – угловая ско-
рость и угловое ускорение.
Угловой скоростью называется величина, которая равна производной по
|
|
|
LM H. |
|
|
|
|
|
|
времени от угла поворота: |
|
|
|
|
|
||||
Модуль угловой скорости равен L |LM| |H|, а его размерность L! |
|||||||||
радс сN . |
L 1 0 |
|
|
H |
|
|
L 3 0 |
|
|
В |
|
|
|
|
|
|
|||
При |
M |
угол поворота |
|
увеличивается, а при |
M |
уменьшается. |
|||
|
технике угловую скорость часто измеряют в оборотах в минуту, обозна- |
||||||||
чая ее буквой «n». Связь между n и ω дается формулой: |
|
|
|||||||
|
|
|
L |
PO OQ . |
|
|
|
|
|
Угловым ускорением называется величина, равная производной по вре- |
|||||||||
мени от угловой скорости: |
|
|
|
|
|
||||
|
|
M |
. |
|
|
|
R |RM| |L | |H7| |
|
|
МодульRM L угловогоH7 |
ускорения равен |
M |
. |
|
|||||
|
|
||||||||

45
Его размерность L! рад сN .
с6
Знаки углового ускорения и угловой скорости позволяют установить является вращениеL ∙ Rзамедленным1 0 или ускоренным.
При M M L ∙вращениеR 3 0 является ускоренным (направления векторов совпадают), а при M M – замедленным (направления противоположны).
Угловая скорость и угловое ускорение характеризуют вращение тела, как целого. Скорости и ускорения отдельных точек тела при этом будут отличаться.
2.3.3 Равномерное и равнопеременное вращение
Равномерным называется такое вращение тела, при котором угловая ско-
рость все время остается постоянной: |
M |
+,* |
. Тогда |
M |
M |
. |
|
||||||
При равномерном вращении |
|
L |
|
. ИнтегрируяR L это0 |
равен- |
||||||||
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
ство, получим уравнение равномерного вращения: |
|
|
|
|
|
|
|||||||
|
|
|
|
EH⁄E L +,* |
|
|
|
|
|
||||
|
|
M |
. |
|
|
|
|
|
|
|
|
|
|
Это |
уравнение определяет величину угла поворота в любой момент време- |
||||||||||||
|
H L ( H |
|
|
|
|
|
|
|
|
|
|
|
|
ни. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Равнопеременным называется вращение тела, при котором величина уг- |
|||||||||||||
лового ускорения все время остается постоянной: |
RM +,* . |
Оно бывает рав- |
|||||||||||
ноускоренным или равнозамедленным. |
|
|
|
|
|
||||||||
Дважды интегрируя равенство |
TU RM +,* , |
получим выражения |
|||||||||||
для угловой скорости и угла поворота, |
то есть уравнения равнопеременного |
||||||||||||
вращения: |
LM RM ( L ; |
H VU 6 ( L ( H , |
|
||
где H и L − начальные значения угла поворота и угловой скорости. |
||
|
2.3.4 Скорость точки вращающегося тела |
|
Рассмотрим твердое тело, совершающее вращение вокруг оси z. |
||
Любая точка М, не лежащая на оси вращения, будет двигаться по окружно- |
||
сти, которая лежит в плоскости, перпендикулярной к оси вращения z. |
||
Рассмотрим, как найти скорость точки М, кото- |
||
рая удалена от оси вращения на расстояние R, если |
||
для вращающегося тела известна угловая скорость |
||
L |
и угловое ускорение . |
Π |
− O |
z R |
|
+ |
|
||
Глядя навстречу оси вращения покажем на ри- |
|
ϕ |
||
R |
|
|
|
|
|
|
|
s |
M |
|
|
|
|
|
|
|
|
Π1 |
R |
|
|
|
v |

46
сунке 2.9 траекторию точки М.
За начало отсчета дуговой координаты s примем точку О, которая лежит в неподвижной полуплоскости П. Подвижную полуплоскость П1 проведем через точку М. Положительное направление отсчета дуговой координаты s пусть будет направлено против часовой стрелки.
Рис. 2.9
Из геометрии известно соотношение между углом и длиной дуги: |
H |
. |
||
Для модулей H L |
найдем скорость точки: |
|
||
Дифференцируя его по времени, |
|
|||
/ |
M . |
|
|
|
соответствующихL скоростей получим:
Модули скоростей точек пропорциональны их расстояниям до оси вращения, а коэффициентом пропорциональности является модуль угловой скорости.
|
|
|
|
|
2.3.5 Ускорение точки вращающегося тела |
|||||
|
Определим ускорение точки М. Из кинематики точки известно, что полное |
|||||||||
ускорение является векторной суммой касательного и нормального ускорений: |
||||||||||
тела |
|
|
4 |
/ |
W |
|
|
|
|
|
|
где |
|
|
4касательное4/ ( 4 , |
ускорение, которое при рассмотрении твердого |
|||||
|
|
|
|
|||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
называют вращательным ускорением, |
|
|
|||||||
|
|
− |
нормальное ускорение, |
которое при рассмотрении твердого тела |
||||||
называют центростремительным или осестремительным ускорением. |
||||||||||
|
В ряде книг вместо 4/и 4 |
применяются обозначения 4ВР и 4ЦС. |
||||||||
|
Алгебраическое значение касательного ускорения: |
|||||||||
|
|
|
|
|
4/ L R |
|
|
|||
|
|
|
|
|
/ |
|
M |
MR. |
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
ε |
|
ω |
R |
|
R |
|
|
|
R |
|
|
|
|
a |
β |
a |
|
|
|
an |
|
|
|
|
n |
τ |
|
|
|
|
β |
|
|
|
|
R |
|
|
|
R |
|
|
|
|
|
a |
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
aτ |
|
a |
|
ω |
|
ε |
|
|
|
|
R |
|
|
|
|
|
Рис. 2.10 |
|||
|
v |
|
|
|
|
|
|
|
|
|
При этом модуль касательного ускорения: 4/ R . |
T6]]6, |
Нормальное ускорение определяется по формуле: 4 5C6 |
47
Откуда 4 L R.
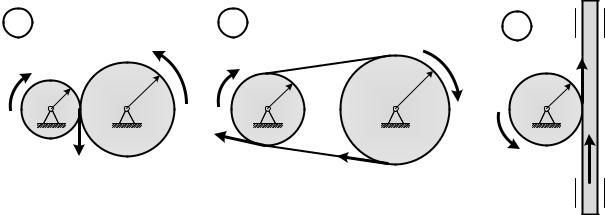
2.3.6Преобразование простейших форм движения тела
Вдвижущихся элементах машин виды движения часто преобразуются. Происходит:
∙преобразование одного вращательного движения в другое, а также ∙преобразование вращательного движения в поступательное (и наоборот). Преобразования эти происходят с помощью ∙зубчатых или фрикционных передач (рис. 2.11 а, в)
∙ременных или цепных передач (рис. 2.11 б)
ω |
|
ω2 |
ω1 |
ω2 |
|
v |
|
1 |
|
|
|
R2 |
|
|
|
R1 |
R |
|
R1 |
R |
|
|
|
2 |
|
|
|
|
|||
v |
|
|
v |
v |
ω |
|
v |
|
|
|
|
|
|
||
|
|
|
Рис. 2.11 |
|
|
|
|
Связи между скоростями двух различных движений называются кинема- |
|
||||||
тическими связями. Они устанавливаются из условия отсутствия проскальзы- |
|
||||||
вания между взаимодействующими телами, то есть из условия равенства скоро- |
|
||||||
стей двух тел в точке их соприкосновения. |
|
|
|
|
|||
Так для рис. 2.11 а, б справедливым является соотношение |
|
|
|
||||
L L |
или |
|
TT^6 ]]6^, |
|
|
|
|
которое получено из условия, что в точке соприкосновения |
(ско- |
|
|||||
рость точки первого тела равна скорости точки второго тела) . |
|
|
|||||
В соответствии с этим соотношением, |
угловые скорости обратно пропор- |
|
|||||
циональны соответствующим радиусам. |
L. |
Для передачи, показанной на рис. в , имеем соотношение: |
2.3.7 Плоскопараллельное движение твердого тела
Задание плоского движения

48
Рассмотрим движение плоской фигуры. Для этого выберем неподвижную систему координат Оху. Выберем на плоской фигуре точку С, которую будем называть полюсом и проведем через нее систему координат, которая будет двигаться вместе с телом. Положение точки С в любой момент времени определяется координатами полюса. Само тело при этом может поворачиваться вокруг полюса. ВеличинуH этого поворота определяет угол (угол между осями х и х').
y |
y1 |
|
x |
|
|
||
|
|
|
1 |
|
xC |
C |
ϕ |
|
|
yC |
|
O |
|
|
x |
|
|
|
|
|
|
Рис. 2.12 |
|
Координаты полюса и угол поворота при движении меняются, то есть зависят от времени. Соответствующие формулы называются уравнениями плоскопараллельного движения:
Из этих уравнений можно найти основные кинематические характеристики
тела при плоском движении: |
|
|
|
|
|||||
|
|
|
|
|
|
||||
∙скорость |
и ускорение |
полюса, |
|
|
|||||
∙угловую скорость` |
|
и угловое4` |
ускорение |
|
тела. |
||||
Важно заметить, |
что плоское движение можно представить как совокуп- |
||||||||
|
L |
|
|
|
|
R |
|
||
ность двух движений: поступательного и вращательного. Угол поворота (H) и |
|||||||||
кинематические характристики вращательной части движения (L и R) не зави- |
|||||||||
сят от выбора полюса, координаты полюса ( ` |
, `) и кинематические характе- |
||||||||
ристики поступательной части движения ( ` и |
4`) зависят от выбора полюса. |
||||||||
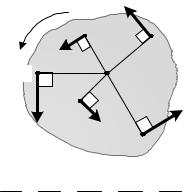
2.3.8 Теорема о сложении скоростей
Скорость любой другой точки плоской фигуры равна векторной сумме скорости полюса и скорости, которую эта точка имеет в относительном вращении этой фигуры вокруг полюса: a ` ( a`.
|
R |
|
|
vM |
R |
|
|
vMC |
R |
|
|
vC |
R |
|
|
vC |
|
|
C |
M |
ω
49
Направление и модуль вектора a` a` определяется по правилам, принятым для вращательного движения:
∙ скорость перпендикулярна отрезку МС и направлена в сторону враще-
ния, ∙модуль скорости вычисляется по формуле Эйлера: a` L a`.
Рис. 2.13
Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется точка Р плоской0. фигуры, скорость которой в данный момент времени равна нулю: b
Такая точка всегда существует. Положение МЦС на движущейся фигуре не является неизменным, в процессе движения его положение постоянно меняется; МЦС может находиться вне тела. Если угловая скорость тела в данный момент равна нулю, то МЦС располагается в бесконечности. В этом случае скорости всех точек тела одинаковы. Движение тела в данный момент времени называют мгновенно поступательным, в отличие от поступательного движения,
при котором L 0 Rв любой |
момент времени. |
|
|
|
|
||||||||||
|
|
Если |
выбрать |
|
в |
качестве полюса МЦС, то |
|||||||||
ω |
|
|
|
|
vD |
скорость произвольной точки М будет равна ско- |
|||||||||
|
E |
|
|
|
|||||||||||
|
R |
|
|
|
D |
рости, которую она имеет в относительном враще- |
|||||||||
|
|
|
|
|
|||||||||||
R |
vE |
B |
R |
|
|
|
|
a b ( ab aР. |
|
||||||
|
|
|
vC |
|
|
|
|||||||||
A |
|
|
|
P |
|
нии вокруг МЦС: |
|
|
|
|
|||||
|
900 |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
vA |
|
vB |
C |
|
|
|
Следовательно: |
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
a направлена перпендику- |
|||||||
vA |
= vB |
= vC |
= vD |
= vE |
|
|
1. |
скорость |
|||||||
|
|
|
|
|
|
|
лярно отрезку РМ в |
сторону вращения; |
|
||||||
PA |
PB |
|
PC |
|
PD |
PE |
|
|
|
||||||
|
|
|
|
2. |
модуль ее в равен a L aР. |
|
|||||||||
|
Рис. 2.14 |
|
|
|
|
|
|
||||||||
|
Нахождение положения мгновенного центра скоростей |
|
|||||||||||||
|
Рассмотрим несколько простых приемов, позволяющих в процессе реше- |
||||||||||||||
(рис. 2.15 а). |
|
|
|
|
|
|
|
L |
|
|
|
А |
|||
ния задач определить местоположение МЦС. |
|
|
|
|
|
||||||||||
|
1) Известна угловая скорость фигуры |
|
и скорость любой ее точки . |
||||||||||||
|
Для определения МЦС надо: |
, на 900 в сторону вращения тела, найти |
|||||||||||||
|
∙Повернув вектор скорости |
||||||||||||||
направление, на котором лежит |
МЦС; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
