
7535
.pdf
10
3) Опорный стержень
Опорным стержнем принято называть невесомый стержень, прикрепляемый с двух сторон с помощью шарниров (рис. 1.8, б). Реакция направлена по линии, которая проходит через центры опорных шарниров.
Эта связь является удерживающей или двухсторонней.
4) Шарнирно-подвижная опора
Такой тип опоры может быть реализован в виде опоры на катках.
R
RA
R R
RA RA
Рис. 1.9
Наличие катков позволяет опоре свободно перемещаться вдоль поверхности, поэтому, реакция перпендикулярна к опорной поверхности. Линия ее действия проходит через центр шарнира.
5) Шарнирно-неподвижная опора
Если тело прикреплено к поверхности (другому телу) с помощью неподвижного цилиндрического шарнира (см. рис. 1.10, а), то реакция имеет неизвестное направление в плоскости действия и угол α может быть любым.
R
В этом случае силу RA неизвестного направления удобно разложить на две
RR
неизвестные силы X A и YA , направленные по координатным осям.
Схематично опора может изображаться в виде двух опорных стержней, неподвижно фиксирующих точку А, как это показано на рис. 1.10,б.
R R
Y R R R
A A YA RA
R |
|
|
|
R |
|
X |
A |
|
|
X A |
Рис. 1.10 |
|
|
|
|
||
R |
R |
R |
|
|
|
|
|
|
|||
При этом RA |
= XA |
+YA |
и R A = X A |
2 + YA |
2 |
Силы X A и YA называются составляющими силы RA по осям х и у.
11
6) Жесткая заделка
Жёсткая заделка препятствует любому поступательному перемещению тела, поэтому направление её реакции заранее определить нельзя и сначала опре-
деляют её составляющие RAX и RAY . Кроме того, жёсткая заделка препятствует повороту телу, поэтому, кроме силы реакции, на тело действует ещё момент заделки , уравновешивающий стремление нагрузок повернуть тело.
R |
R |
|
RAY |
|
|
R |
A |
|
|
|
|
M A |
|
|
|
R |
|
RAX
Рис. 1.11
1.3Вектор силы
1.3.1Проекции силы
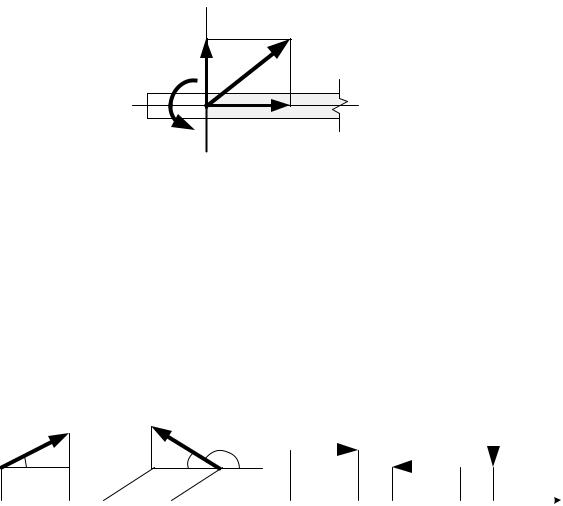
Проекцией вектора на ось называется скалярная величина равная произведению модуля вектора на косинус угла между направлением силы и положительным направлением оси.
Рассмотрим некоторые частные случаи проектирования вектора на ось:
|
|
|
|
|
|
|
R |
R |
R |
R |
|
|
|
F |
|
F |
F |
|
|
|
|
||
|
α |
F |
|
R |
|
|
|
|
|
|
|
F |
|
|
|
α |
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx = F cosα |
Fx = F cosα = −F cosϕ |
Fx = F |
Fx = −F |
Fx = 0 |
|||
Рис. 1.12
1.3.2 Распределенные силы
Понятие силы, приложенной в точке, есть идеализация, так как взаимодействие тел реально всегда происходит по некоторой площадке или даже по объему (как у гравитационных сил).
Сосредоточенная в точке сила всегда представляет собой равнодействующую некоторой распределенной силы.
В механике рассматриваются три вида моделей распределенных сил:

12
1)силы, распределенные вдоль линии;
2)силы, распределенные по поверхности;
3)силы, распределенные по объему.
Силы, распределенные вдоль линии
Сила, распределенная вдоль линии, характеризуется ее интенсивностью q,
которая является мерой величины силы, приходящейся на единицу длины (на погонный метр) и измеряется в Н/м.
Величина интенсивности может быть переменной q = q( x) (рис. 3.8, а) или постоянной q = const (рис. 3.8, б).
q |
q |
x |
x |
O |
O |
l |
l |
l |
Q = ∫ q ( x ) dx |
|
Q = ql |
|
|
|
0 |
|
|
Рис. 1.13
В общем случае, когда сила на участке (0, l ) распределена по произволь-
ному закону q = q( x) , ее равнодействующая Q должна быть вычислена как инте-
грал. Линия действия равнодействующий Q проходит через центр тяжести подграфика интенсивности, положение которого неизвестно.
Рассмотрим частные случаи.
Равномерно распределенная сила
Если интенсивность постоянна q = const (см. рис. 1.13, б), то ее равнодействующая равна и приложена посередине участка распределения.
Сила, интенсивность которой меняется по линейному закону
В этом случае (рис. 1.14, а) соответствующий интеграл дает Q = 1 ql, и рав-
2
нодействующая будет проходить на расстоянии 2l/3 от вершины треугольника интенсивности и на расстоянии l/3 от его основания. Аналогично определяется равнодействующая, если с ростом координаты х интенсивность убывает от qmax до нуля.

13
q |
qMAX |
q |
|
q2 |
|
|
|||
|
|
q1 |
|
|
O |
x |
O |
|
x |
l |
|
l |
||
R |
R |
R |
||
Q |
|
Q1 |
Q |
|
|
|
|
2 |
|
2 |
l |
1 |
l |
1 |
l |
1 |
l |
1 |
l |
|
|
|
|||||||||
|
|
|
|
|||||||
|
|
|
|
|
||||||
3 |
|
3 |
3 |
3 |
3 |
Рис. 1.14 |
||||
|
|
|
|
|
|
|
|
|||
Сила, интенсивность которой меняется по линейному закону от q1 до q2
В этом случае (рис. 1.14, б) силу удобно разбить на две распределенные силы, рассмотренные в пункте 2 (на рисунке разбиение показано штрихом).
Q = |
1 |
q l, и |
Q |
|
= |
1 |
q |
|
l, |
2 |
|
|
|
||||||
1 |
1 |
|
2 |
2 |
|
2 |
|
||
Тогда исходная распределенная сила заменится двумя силами, линии действия которых делят участок (0, l ) на три равные части.
1.3.3 Сходящаяся система сил
Сходящейся системой сил называются совокупность сил, линии действия которых пересекаются в одной точке − точке схода системы.
Простейшая система сходящихся сил (две силы) была рассмотрена в аксиоме параллелограмма сил (см. рис.1.15), где указывалось, что их равнодействующая изображается диагональю параллелограмма, построенного на этих силах как на сторонах.
R |
R |
F1 |
R |
R
F2
Рис. 1.15
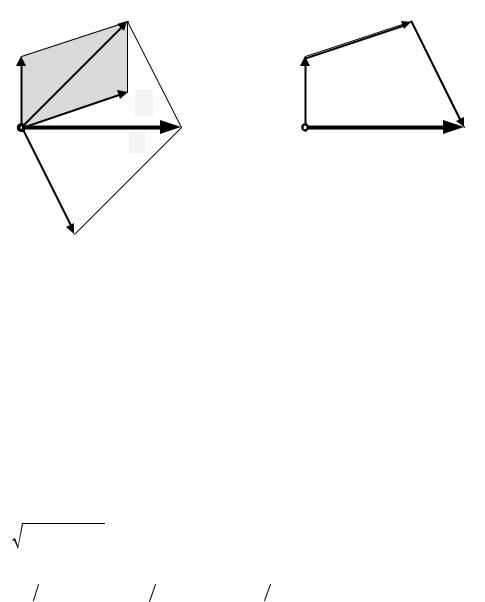
Рассмотрим систему трех сил ( R R R ), приложенных в точке О.
F1, F2 , F3
14
R |
|
|
P |
|
|
R |
|
R |
F1 |
|
F |
|
|
2 |
|
R |
R |
|
F1 |
|
R |
F |
|
F2 |
|
3 |
|
|
|
R |
|
R |
|
R |
|
R |
|
R
F3
Рис. 1.16
Система сходящихся сил имеет равнодействующую, приложенную в точке пересечения линий действия сил, которая геометрически равна главному вектору этой системы сил. Если для какой-то системы сил равнодействующая существует, то она геометрически всегда равна главному вектору. Отсюда следует, что проекции равнодействующей сходящейся системы сил определяются так же, как и проекции главного вектора:
n |
n |
n |
Rx = ∑ Fix |
Ry = ∑ Fiy |
Rz = ∑ Fiz . |
i=1 |
i =1 |
i=1 |
Модуль равнодействующей равен:
R = 
 Rx2 + Ry2 + Rz2 ,
Rx2 + Ry2 + Rz2 ,
а ее направляющие косинусы определяются по формулам:
nx = Rx R, |
ny = Ry R, |
nz = Rz R. |
1.3.4 Условия уравновешенности сходящейся системы сил
Система сходящихся сил эквивалентна одной силе, которая по определе-
нию является равнодействующей:
≡ , , … , .
В общем случае сходящаяся система не является уравновешенной. Исключение составляет случай, когда равнодействующая, а следовательно и главный вектор этой системы сил равны нулю.
Равнодействующая сходящейся системы геометрически равна ее главному
R R n R
вектору R = R = ∑ Fi , который приложен в точке схода системы.
i =1
Отсюда следует, что для равновесия системы сходящихся сил, необходимо и достаточно, чтобы выполнялись следующие условия:
15
1) В векторной форме главный вектор системы сил должен быть равен ну-
R |
= 0 или |
n R |
= 0 |
лю: R |
∑ Fi |
i=1
2)В геометрической форме силовой многоугольник должен быть замкнут.
3)В аналитической форме сумма проекций сил на каждую из координатных осей должна быть равна нулю:
|
|
∑ Fix |
= 0 |
|
|
n |
|
R x |
= 0 |
i=1 |
|
|
или |
n |
|
R y |
= 0 |
∑ Fiy |
= 0 |
|
|
||
|
|
i=1 |
|
1.3.5 Теорема о трех силах
Теорема:
Если твердое тело находится в равновесии под действием трех сил, и линии действия двух из них пересекаются в некоторой точке, то и линия действия третьей силы проходит через эту точку.
Примечание:
Теорема о трех силах дает необходимое условие равновесие, без которого равновесие в принципе невозможно. Достаточным условием является замкнутость силового треугольника.
1.4Моменты силы
1.4.1Момент силы относительно точки
Величина модуля и направление силы характеризуют действие силы в том случае, если она придает какому-либо телу поступательное движение. Вращательный эффект силы по отношению к некоторой точке или оси учитывает другая характеристика – момент силы.
Моментом силы F относительно некоторой точки О называется величина
R ( R )
MO F , равная векторному произведению радиус-вектора, проведенного из
данной точки в точку приложения силы, на саму эту силу :
R R |
R |
R |
MO (F ) = r |
× F . |
|
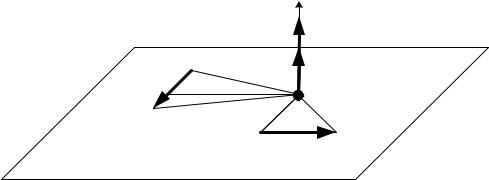
Вектор-момент силы перпендикулярен плоскости, проведенной через линию действия силы и точку О (рис. 1.17), и направлен так, чтобы, глядя навстречу ему, видеть силу, стремящейся повернуть плоскость против часовой стрелки (правило «правого винта»).

16
|
|
|
|
|
|
|
|
|
R |
R |
|
|
|
|
|
|
|
|
|
MO |
(F ) OAB |
||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
π 2 |
|
|
|
|
|
|
|
|
|
|
R |
h |
|
|
|
|
|
|
|
|
|
B |
F |
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.1.17 |
|
|
|
|
Модуль векторного произведения: |
|
|
|
|
|||||||
|
R |
R |
|
= r × F × sin α , |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
r |
´ F |
|
где r × sin α = h или MO (F ) = F ×h . |
|||||||
Модуль момента силы относительно точки равен произведению модуля силы на ее плечо.
Плечом силы называется кратчайшее (по перпендикуляру) расстояние от точки до линии действия силы.
Размерность модуля момента силы [M]= Нм. Момент силы относительно точки равен нулю только в том случае, когда ее плечо равно нулю, т. е. когда линия действия силы проходит через эту точку. Момент силы не зависит от того, где взята точка приложения силы на линии ее действия. Модуль момента силы равен удвоенной площади треугольника, для которого сила является основанием, а плечо высотой.
1.4.2 Момент силы относительно оси
Моментом силы |
R |
|
F относительно некоторой оси z называется скалярная |
||
R |
|
|
величина M z (F ), равная проекции на эту ось момента силы, вычисленного от- |
||
носительно какой-либо точки О этой оси: |
|
|
|
M z (F ) = (MO (F )) |
|
|
R |
R R |
z
1.4.3 Главные моменты сил
системы сил относительно некоторой точки О или оси называется векторная сумма моментов всех сил системы относительно той же точки или оси.
17
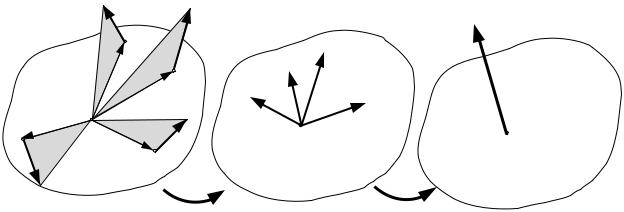
Главный момент относительно центра О выражается формулой:
O |
|
∑ |
|
O ( i ) |
|
∑( i |
i ) |
|
R |
= |
n |
R |
R |
= |
n |
R |
R |
M |
|
M F |
|
r |
×F . |
|||
|
|
i=1 |
|
|
|
i=1 |
|
|
|
R |
|
|
|
|
|
F1 |
|
|
|
|
|
|
R |
|
|
|
|
|
F2 |
|
|
|
|
R |
|
|
|
|
|
r1 |
R |
R |
|
|
|
|
R |
R |
||
|
|
MO (F2 ) |
|||
|
R |
MO |
(Fi ) |
||
|
r2 |
|
|
|
|
R |
O |
R |
R |
|
|
rn |
|
MO (F1 ) |
R |
R |
|
|
R |
R |
O |
MO (Fn ) |
|
|
ri |
F |
|
|
|
|
|
i |
|
|
|
R
Fn
R |
n R R |
MO |
= ∑M O (Fi ) |
i=1
O
Рис. 1.18
Главный момент относительно некоторой оси L выражается формулой:
L |
∑ |
L ( i ) |
M = |
n |
R |
|
M F . |
|
|
i=1 |
|
Кроме того, главный момент системы сил относительно оси равен проекции на эту ось главного момента системы сил, определенногог относительно некоторой точки этой оси.
1.4.4 Аналитический способ определения главного момента
Для определения главного момента системы сил относительно центра О необходимо сложить n моментов сил:
R |
n R R |
MO |
= ∑MO (Fi ) |
i=1
Поскольку равны векторы, стоящие в левой и правой частях последнего равенства, должны быть равны и их проекции на любую ось.
Спроектируем это равенство на оси х, у, z:
|
n |
R |
|
|
|
||
Mx |
= ∑M x (Fi ), |
||
|
i=1 |
R |
|
|
n |
|
|
My = ∑M y (Fi ), , |
|||
|
i=1 |
|
|
|
n |
R |
), |
Mz |
= ∑M z (Fi |
||
|
i=1 |
|
|
где Mx , My ,Mz − главные моменты сил системы относительно коорди- |
|||
натных осей, проходящих через центр О,

18
R |
R |
R |
|
|
|
|
а Mx (Fi ), M y (Fi ), Mz (Fi ) − моменты сил системы относительно тех же осей. |
||||||
|
|
|
|
|
||
Модуль главного момента: |
MO = |
|
M2x +M2y +M2z |
|||
и его направляющие косинусы: lx =Mx MO , |
ly =My MO , lz =Mz MO , |
|||||
Рассмотрим частный случай, когда главный момент равен нулю. В этом случае модуль главного момента будет равен нулю:
MO = 0 или 
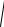 M2x +M2y +M2z = 0
M2x +M2y +M2z = 0
Последнее равенство возможно только если все слагаемые под корнем равны нулю, то есть если
MxMyMz
|
∑M x (Fi ) |
|
|
n |
R |
= 0 |
i=1 |
|
|
n |
R |
= 0 |
или ∑M y (Fi ) |
|
= 0 |
i=1 |
|
|
n |
R |
|
∑M z (Fi ) |
|
|
i=1 |
|
=0,
=0,
=0.
Главный момент системы сил относительно некоторого центра О будет равен нулю в том случае, когда все три суммы моментов исходных сил системы относительно осей, проходящих через центр О, будут равны нулю.
1.4.5 Зависимость главного момента от выбора точки приведения
Зависимость главного момента от выбора точки приведения:
M =M + R ×R
B A r0 .
Если главный вектор некоторой системы сил равны нулю (R = 0 ), то глав-
ный момент для всех точек пространства будет одинаков, поскольку MB =MA. в
соответствии с формулой. Если для некоторого центра A главный момент и главный вектор системы равны нулю (MA =0 и R = 0 ), то главный момент будет равен нулю и относительно любого другого центра.
1.4.6 Моменты сил, расположенных в одной плоскости
Плоской системой называется система сил, линии действия которых лежат в одной плоскости.
При расположении всех сил системы на одной плоскости вектора моментов сил системы относительно точек плоскости расположены к этой плоскости перпендикулярно. Для указания их направления достаточно одного знака − знака проекции вектора на ось z, перепендикулярную к плоскости.
19
|
ось z |
|
|
|
R |
R |
|
|
M B (F1 ) |
||
|
R |
R |
|
R |
M B (F2 ) |
||
F1 |
|||
h1 |
|
||
|
|
||
|
B |
|
|
|
h2 |
|
|
|
R |
|
|
|
F2 |
|
|
Рис. 1.19
По этой причине при рассмотрении плоских систем под моментом силы относительно точки на самом деле понимают скалярную величину: момент силы относительно оси z, проходящей через моментную точку перпендикулярно к плоскости действия сил.
|
R |
R |
То есть |
MB (F ) = MZ (F ) |
|
Величина момента равна произведению силы на плечо:
( R ) = ± .
MB F Fh
Если момент направлен против часовой стрелки − он считается положительным. При переходе к векторному представлению такое правило знаков соответствует знаку проекции вектор-момента на ось z.
Сложив моменты всех сил системы относительно точки О, получим скалярную величину – главный алгебраический момент плоской системы сил от-
n |
R n |
R |
носительно точки О: MO = ∑ MO (Fi ) = ∑ M Z (Fi ). |
||
i=1 |
i=1 |
|
1.5Теория пар
1.5.1Сложение двух параллельных сил
До сих пор мы изучили лишь вопрос о сложении сходящихся сил. Перейдем теперь к определению равнодействующей системы параллель-
ных сил, остановившись сначала на случае двух параллельных сил, приложенных в точках А и В.
Здесь возможны два варианта:
1)силы направлены в одну сторону (рис. 1.20 а).
