
6848
.pdf
40
|
|
R |
|
|
|
τ − единичныйвектор, |
|
R |
|
направленный в положительном |
|
|
|
||
− |
|
направлении дуговой координаты |
|
C |
O |
О − начало отсчета |
|
|
R |
дуговой координаты |
|
α |
τ |
||
|
|||
+ |
|
|
|
M |
|
S − дуговая |
|
|
|
||
R |
|
координата |
|
τ |
|
|
Рис.2.6
2. Определяем положение точки М при t=2c (точку М1).
Из геометрии известно соотношение между центральным углом окружности и длиной соответствующей дуги: o ]r.
Определим дуговую координату для момента времени t=2c.
W|QKXU Xp ∙ X p ∙ XX p p Zp.
Это значение дуговой координаты соответствует центральному углу
] rW ZpX XiRR.
Показываем точку М1 на рисунке.
R |
|
|
R |
R |
|
|
aτ |
M1 τ |
v |
|
|||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
aτ ×vτ < 0 - движение |
R |
|
|
R |
|
||
|
|
|||||
|
|
an |
|
|
||
a |
|
|
− |
замедленное |
||
|
|
|
|
|
|
|
3π |
|
|
C |
|
O |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
Рис.2.7
3. Определяем скорость точки.
Определяем проекцию скорости на единичный вектор касательной:

41
. |
p |
, |
_d W. Xp X |
Q |
|
|
. p |
м. |
_d|QKXU Xp X |
∙ X p Z. ^ с |
|
_d s R, следовательно, вектор скорости направлен в сторону положительного от- |
||
счета дуговой координаты (вправо). Модуль скорости имеет то же значение, по- |
|||
скольку _ |_d |
|. |
|
|
4. Определяем ускорение точки. |
|||
Определяем проекцию ускорения на единичный вектор касательной: |
|||
. p |
|
м |
. |
|
|
||
!d W9 X |
^. Ti UX |
||
Определяем проекцию ускорения на единичный вектор нормали:
!\ _gX Z.^X X . tZ смX.
Определяем модуль ускорения (полное ускорение):
! !Xd !X\ √^. TiX . tZX T. ^i смX. 5. Определяем характер движения.
Проекции _d и !d имеют разные знаки.
Это говорит о том, что вектора *# и *#!d направлены в разные стороны.
Таким образом, движение точки в заданный момент времени t=2c является за-
медленным.
Ответ: _ Z. ^ мс , !d ^. Ti UмX , !\ . tZ смX, ! T. ^i смX
2.2 Движение твердого тела
Простейшими видами движения твердого тела являются поступательное и вращательное движения.
Поступательным движением называется движение, при котором любой отрезок, принадлежащий телу, перемещается, оставаясь параллельным своему первоначальному направлению. Поступательное движение твердого тела полностью определяется движением какой-либо его точки, например центра тяжести.
Вращательным движением называется движение тела, при котором все точки
тела, лежащие на некоторой прямой, остаются неподвижными. |
|
|
|
Угловой скоростью называется лежащий на оси вращения вектор **#ω, проекция ко- |
|||
торого на эту ось равна производной по времени от угла поворота: |
ωv |
φ. |
|
Модуль угловой скорости равен |
ω |ωv| |φ.| , а |
его |
размерность |
xωy радс с}D. |
|
|
|
|
|
42 |
При ~• s 0 угол поворота € увеличивается, а при ~• • 0 уменьшается. |
||
Угловым ускорением называется величина ε#, равная производной по времени от |
||
угловой скорости: |
ε# **#ω. |
|
При этом проекция вектора углового ускорения на ось z будет равна: |
||
ƒ• ~. €9 |
|
|
• |
. |
|
Модуль углового ускорения равен ƒ |ƒ•| |€9|, а его размерность xƒy радP1 |
||
с} . При ~• ∙ ƒ• |
s 0 вращение является ускоренным (направления векторов совпа- |
|
дают), а при ~• |
∙ ƒ• |
• 0 – замедленным (направления векторов противоположны). |
Скорость точки |
вращающегося тела определяется по формуле Эйлера: |
|
) ~ . |
|
|
Полное ускорение точки вращающегося тела является векторной суммой каса-
тельного и нормального ускорений:
*#a *#a… *#a†,
где a… ε R - касательное ускорение, которое при рассмотрении твердого тела называют вращательным ускорением,
/? ~ R - нормальное ускорение, которое при рассмотрении твердого тела называют центростремительным или осестремительным ускорением.
2.3Преобразование вращательного движения
Вдвижущихся элементах машин часто происходят преобразования движений: ∙ преобразование одного вращательного движения в другое, ∙ преобразование вращательного движения в поступательное
(и наоборот).
Преобразования эти происходят с помощью
∙зубчатых или фрикционных передач,
∙ременных или цепных передач.

43
ω |
ω2 |
ω1 |
|
ω2 |
v |
1 |
|
|
R2 |
|
|
R1 |
R |
R1 |
|
R |
|
2 |
|
|
|||
v |
|
v |
|
ω |
v |
|
|
v |
|
|
Рис.2.8
Связи между скоростями двух различных движений устанавливаются из условия отсутствия проскальзывания между взаимодействующими телами, то есть из условия равенства скоростей двух тел в точке их соприкосновения.
Так, справедливым является соотношение
~D D ~ или
которое получено из условия, что в точке соприкосновения )D ) (скорость точки первого тела равна скорости точки второго тела).
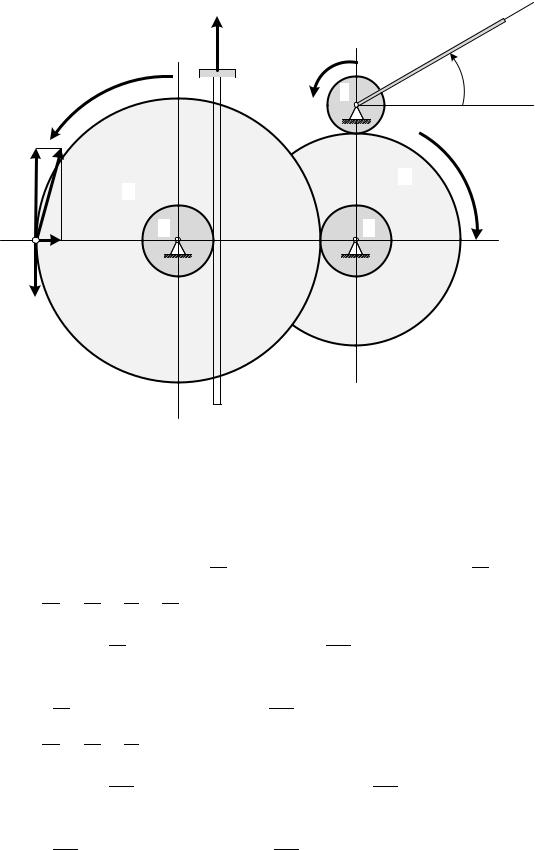
Задача 2.7. Преобразование движений твердого тела В механизме домкрата рукоятка А отклоняется на угол ‹, который изменяется в
пределах от -300 до +300 по закону ‹ p` W[\ ŒpQZ •. Рукоятка А жестко соединена с
шестерней 1, то есть ‹^ ‹. Шестерни 2, 3, 4, 5, вращаясь, толкают зубчатую рейку В, для которой движение вниз запрещено.
Определить скорости и ускорения деталей 1, 2, 3, 4, 5 и В, если известно, что |
|
rT ^` см , а |
количество зубьев на шестеренках равно: Ž^ `, ŽX X , ŽZ |
h, Ž ZX. При |
t=1c определить скорость и ускорение рейки В и точки М, если |
известно, что r h см.
44
|
|
vB |
ω > 0 |
ω4 |
= ω5 |
> 0 |
1 |
|
|||
|
|
B |
1 |
R |
R |
|
|
aM |
2 |
||
aMτ |
|||
|
4 |
|
|
M |
5 |
3 |
|
|
R |
|
|
|
an |
|
|
|
M |
|
|
R |
|
|
|
vM |
|
|
ϕ > 0
ω2 = ω3 < 0
Рис.2.9
Решение:
Определяем скорости и ускорения элементов механизма, принимая положительное направление поворота против часовой стрелки.
Рукоятка А жестко соединена с шестерней 1, поэтому
p |
pQ |
, |
|
^ |
pX |
pQ |
|
^ |
|
^ |
^ |
pZ |
pQ |
|
‹^ ‹ ` W[\ Œ Z • |
|
|
^h UVW Œ Z •, • |
|
|
|
•. |
|||||||
|
•^ ‹. |
|
•. |
‹9 T W[\ Œ Z |
||||||||||
Из условия |
••X^ rr^X ŽŽ^X X` найдем, |
что |
•X ^ •^, откуда следует, что |
|||||||||||
^ |
|
|
pX |
pQ |
|
X |
|
pZ |
pQ |
|
|
|
||
•X •^ iX UVW Œ Z •, |
|
|
|
|
|
|
|
|
|
|||||
•X •. X^` W[\ Œ Z •. |
|
|
|
|||||||||||
Шестерни 2 и 3 связаны жестко, поэтому |
pZ |
|
|
pQ |
|
|
|
|
|
|||||
|
pX |
|
pQ |
|
|
|
|
|
|
|
|
|
||
•Z •X iX UVW |
Œ Z •, |
•Z •X X^` W[\ |
Œ Z •. |
|
|
|
|
|||||||
Из условия |
••Z rrZ ŽŽZ ZXh найдем, |
что |
• ^ •Z, откуда следует, что |
|||||||||||
^ |
|
|
pX |
pQ |
|
|
|
|
pZ |
pQ |
|
|
|
|
• •Z Xhh UVW Œ Z •, |
|
|
|
|
|
|
|
|
||||||
• •. h` W[\ Œ Z •. |
|
|
|
|||||||||||
Шестерни 4 и 5 связаны жестко, поэтому |
pZ |
|
|
pQ |
|
|
|
|
|
|||||
|
pX |
|
pQ |
|
|
|
|
•. |
|
|
|
|
||
•T • Xhh UVW Œ Z •, |
•T • h` W[\ Œ Z |
|
|
|
|
|||||||||

45
Скорость рейки В при •T • R будет равна нулю (движение вниз отсутствует), а
при •T s R находится из условия _‘ •TrT:
_‘ •TrT XhhpX UVW ŒpQZ • ∙ ^` p^hX UVW ŒpQZ •.
При этом ускорение рейки В будет равно
!‘ _.‘ pTZ W[\ ŒpQZ •.
При t=1c |
определяем скорость и ускорение рейки В. |
|||||||||||||||||||||
_‘|QK^ |
pX |
p |
pX |
^ |
|
|
|
м |
|
|
|
|||||||||||
^h UVW ŒZ• ^h ∙ X R. Xi с. |
м |
|
||||||||||||||||||||
!‘|QK^ |
pZ |
p |
|
pZ |
√Z |
|
|
|||||||||||||||
|
|
|
W[\ ŒZ• |
|
|
|
|
∙ |
|
|
|
|
R. ti |
|
. |
|
||||||
T |
T |
|
X |
сX |
|
|||||||||||||||||
При t=1c |
определяем скорость и ускорение шестерни №4. |
|||||||||||||||||||||
• |QK^ |
pX |
p |
|
|
|
pX ^ |
рад |
|
||||||||||||||
|
|
UVW ŒZ |
• |
|
|
∙ X R. R^i |
с |
, |
||||||||||||||
Xhh |
Xhh |
|||||||||||||||||||||
• |QK^ |
|
pZ |
p |
|
|
|
pZ |
|
|
|
√Z |
|
|
рад |
||||||||
|
W[\ ŒZ• |
|
∙ |
|
R. RZ^ |
сX . |
||||||||||||||||
h` |
h` |
X |
||||||||||||||||||||
При t=1c |
определяем скорость и проекции ускорения точки М по формулам: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uм |
, |
|
|
|
|
_Мd • r R. R^i ∙ h R. h^` с |
|
|
|
|||||||||||||||||||
!Мd • r R. RZ^ ∙ h ^. hh смсX , |
|
|
|
|||||||||||||||||||
!М\ •Xr R. R^iX ∙ h R. R^Zt смсX . |
|
|
|
|||||||||||||||||||
При этом модуль ускорения точки М будет равен:
!“ b$!dМ&X $!\М&X r b•X • h√R. RZ^X R. R^i ^, hh смсX . Ответ: _‘|QK^ R. Xi мс, !‘|QK^ R. ti смX, _М R. h^` Uмс , !“ ^, hh смсX .
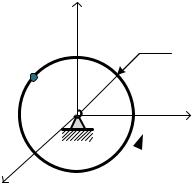
Задача 2.8. Преобразование движений твердого тела Два шкива соединены ременной передачей. Точка А одного из шкивов имеет ско-
рость ) 20 см⁄с. Определить скорость точки В другого шкива.
R
v A
A |
|
C |
D |
|
|
r |
r |
|
2r |
B |
|
|
|
r / 2
46
Рис.2.10
Решение:
Зная скорость точки А можно найти угловую скорость левого шкива:
~лев ) ⁄2".
Умножив эту угловую скорость на расстояние до точки С, найдем ее скорость, ко-
торая в свою очередь будет равна скорости точки D:
)” ~лев ∙ " ) ∙ "⁄2" ) ⁄2 )•.
Поделив скорость точки D на расстояние до оси вращения, получим угловую скорость правого шкива: ~прав )•⁄" ) ⁄2".
Скорость точки В получим, умножая угловую скорость ~прав на расстояние "⁄2:
)– ~прав ∙ $"⁄2& ) ∙ $"⁄2&⁄2" ) ⁄4 20⁄4 5$ мс}D&.
Ответ: )– 5 мс}D.
ЗАДАЧА 2.9. Вращательное движение твердого тела Диск радиуса R=10 см вращается вокруг оси Ох
закону € 2 %O, где € ─ угол поворота тела в дианах (рис.2.11).
Найти величину нормального ускорения точки A момент времени t=2c.
x
по
z
ра-
R
А в
O |
y |
|
 ϕ (t )
ϕ (t )
Решение: |
Рис.2.11 |
Дифференцируя по времени закон вращательного движения, получим угловую
скорость диска, а затем и угловое ускорение вращающегося тела:
~— €. 3%.
Подставляя в полученное выражения значение времени, получим, что при t=2 c |
||||
угловая скорость будет равна: |
~— 3 ∙ 2 |
12 $с}D&. |
||
Теперь нормальное ускорение точки А, лежащей на краю диска, можно найти |
||||
по формуле: |
/? |
~ |
12 ∙ 10 1440 |
$см ∙ с} &. |
Ответ: /? 1440 |
$см ∙ с} & |
|
||
ЗАДАЧА 2.10. Вращательное движение твердого тела
Тело равномерно вращается вокруг оси z с угловой скоростью ~ 6 с}D.

47
На какой угол повернется тело за время t =2 с?
Решение:
По условию задачи вращение тела является равномерным. Поэтому, угол, на кото-
рый тело повернется за некоторый промежуток времени, следует искать по форму-
ле: € ~% 6 ∙ 2 12 $рад&.
Ответ: € 12 рад.
2.4 Плоскопараллельное движение твердого тела
Плоскопараллельным или плоским движением называется движение твердого тела, при котором его точки перемещаются в плоскостях, параллельных некоторой неподвижной плоскости.
Скорость точки плоской фигуры равна векторной сумме скорости полюса и скорости, которую эта точка имеет в относительном вращении этой фигуры вокруг по-
люса:
)#˜ )#” )#˜”.
Если выбрать в качестве полюса МЦС, то скорость произвольной точки М будет |
|
равна: |
)#˜ )#™ )#˜™ )#˜Р. |
Мгновенным центром скоростей (МЦС) называется точка Р плоской фигуры, скорость которой в данный момент времени равна нулю: )™ 0. Такая точка всегда существует.
Скорость произвольной точки М плоской фигуры равняется скорости, которую она имеет в относительном вращении вокруг МЦС.
Ускорение точки плоской фигуры равно векторной сумме ускорения полюса и ускорения, которое имеет эта точка в относительном вращении фигуры вокруг по-
люса:
/#˜ /#” /#˜” /#” /#˜”< /#˜”? .
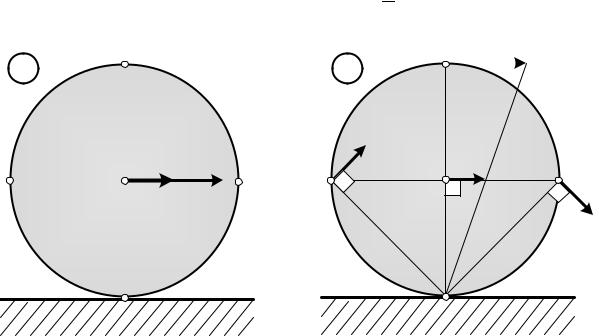
Задача 2.11. Плоскопараллельное движение твердого тела
Пусть колесо радиусом R=1м катится без скольжения по горизонтальной плоскости. Скорость центра колеса _R ^ мс , ам ускорение центра колеса по направлению совпадает со скоростью и равно !R ^ сX.
48
Определить скорости и ускорения точек А, В, С, Р, расположенных на ободе колеса.
Решение:
1. Определение скоростей МЦС колеса – точка Р. Относительно точки Р колесо вращается по часовой стрел-
ке. Соединим точку Р с точками А, В, С и покажем направления скоростей в сторону вращения по перпендикуляру к отрезкам АР, ВР, СР.
|
Угловую скорость колеса получим из формулы, которая связывает угловую ско- |
|||||
рость со скоростью центра колеса: |
_R • ∙ r, |
из которой получается, что • |
||||
_R |
^ ^U. |
|
|
|
|
|
r |
|
|
|
|
|
|
|
Модули скоростей получим по формуле Эйлера _“š • ›“š: |
м |
||||
|
м |
|
м |
; |
|
|
|
_œ • ∙ r√X √X с ; |
_‘ • ∙ Xr X с |
_š • ∙ r√X √X с. |
|||
2. Определение ускорений Расстояние от точки О до МЦС (точки Р) всегда постоянно. Кроме того точка О
движется прямолинейно. В этом случае угловое ускорение можно найти следующим |
||||||||||||||
образом: • •. |
l |
Π|
_ž |
• _r.ž !rž. |
|
|
|
|
|
|
|
|
|
|
lQ |
žŸ |
• |
!ž |
|
^ |
м |
^ радс . |
|
|
|||||
То есть в данный момент времени: |
сX |
|
|
|||||||||||
r |
^м |
R |
||||||||||||
B |
|
|
|
|
|
B |
vB |
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
vA |
|
R |
|
A |
O |
C |
A |
O |
vO |
C |
|
|
|
||||
|
R |
|
|
|
||
|
R |
|
|
|
|
|
|
aO |
vO |
|
|
|
|
R vC
P P
Рис.2.12
Выберем в качестве полюса центр колеса (точку О) и используем для определения
ускорения произвольной точки М теорему о сложении ускорений:
*#!“ *#!ž *#!“ž *#!ž *#!d“ž *#!\“ž.
49
Вращательные ускорения точек A, B, C, P во вращении колеса относительно полюса О по модулю будут одинаковы и направлены перпендикулярно к соответствующему радиусу в сторону углового ускорения:
!dŸž !œžd !d‘ž !dšž • ∙ r ^ U^X ∙ ^м ^ UмX.
Нормальные ускорения точек A, B, C, P во вращении колеса относительно полю-
са О по модулю будут одинаковы и направлены к центру колеса:
!\Ÿž !œž\ !\‘ž !\šž •X ∙ r ^X U^X ∙ ^м ^ UмX.
Суммируя в |
каждой точке три вектора ускорения по формуле |
||||
!*#“ !*#ž !*#“žd |
!*#“ž\ |
, получим, что |
|||
!Ÿ !š ^ |
м |
и |
!А !В √^X XX √T |
м |
. |
сX |
сX |
||||
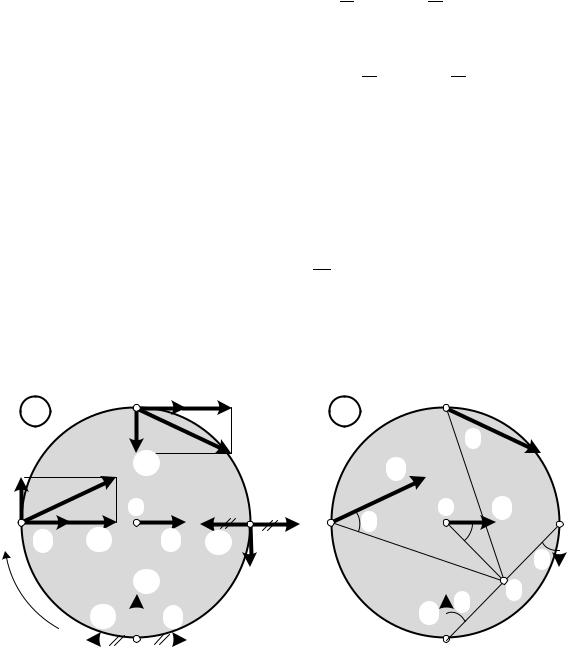
Если на середине отрезка СР отметить точку Q, то можно заметить, что: Ускорения в точках, расположенных на одинаковых расстояниях от точки Q
(точках Р, О, С) одинаковы по величине;
Ускорения в точках, расположенных на разных расстояниях от точки Q пропор-
циональны расстояниям до этих точек Œžœ !!žœ √T•;
Ускорения в точках A, B, C, P направлены таким образом, что составляют одинаковый угол ¢ с отрезками, соединяющими эти точки с точкой Q;
Ускорение в самой точке Q при этом равно нулю.
|
R |
aτBO |
|
B |
aO |
B |
 β
β
a |
τ |
aBOn |
R |
AO |
|
aA |
|
|
|
|
A |
O |
|
C |
A |
β |
O |
|
R |
|
|
|
||
R |
n |
|
R |
|
β |
|
aO |
aO |
an |
|
|||
aAO |
a |
|
||||
|
|
|
CO |
O |
|
|
ε |
aPOn |
aCOτ |
|
β |
|||
|
aτ |
|
R |
|
R |
|
|
|
|
|
|||||
|
|
a |
|
aP |
|
|
|
|
PO |
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R aB
R
aO C
β  R aC
R aC
Q |
aQ = 0
P |
|
P |
|
|
|
Рис.2.13
Точка тела Q, ускорение которой в данный момент равно нулю, называется мгновенным центром ускорений.
