Энергия стационарного магнитного поля

Общее выражение для энергии магнитного поля, сосредоточенной в некотором объеме , остается справедливым и в случае стационарных процессов:

. (10)

Формулу (10) можно преобразовать таким образом, чтобы магнитная энергия была выражена через токи, создающие магнитное поле. Для этого заменим в (10) вектор его представлением через векторный потенциал . Используя тождество

,

получаем

. (11)

Первый интеграл в уравнении (11) преобразуем в поверхностный интеграл, используя теорему Остроградского—Гаусса, а во втором интеграле выразим через плотность токов с помощью равенства . Тогда уравнение (11) примет вид

, (12)

где — поверхность, ограничивающая объем .

Выберем в качестве поверхности сферу радиуса и устремим к бесконечности, т. е. распространим интегрирование в (12) на все пространство.

Любая пространственно ограниченная система токов, как следует из выведеных ранее формул, создает магнитное поле, напряженность и векторный потенциал которого при убывают пропорционально и соответственно (или еще быстрее). При этом поверхность возрастает пропорционально . Следовательно, в пределе при первый интеграл в уравнении (12) будет равен нулю. В результате получим

. (13)

B отличие от исходного выражения (10) интегрирование в (13) распространяется лишь на ту область пространства , в которой имеются токи. В ф-ле (13) можно исключить векторный потенциал . Для этого нужно заменить вектор его представлением в виде интеграла

.

В случае линейных токов выражение для магнитной энергии упрощается. Рассмотрим сначала уединенный контур Г с током . Формула (13) для этого контура принимает вид

. (14)

Применим к интегралу теорему Стокса:

, (15)

где — магнитный поток через поверхность , опирающуюся на контур Г. Подставляя ф-лу (15) в (14), получаем

. (16)

В случае контуров выражение для магнитной энергии записывается следующим образом:

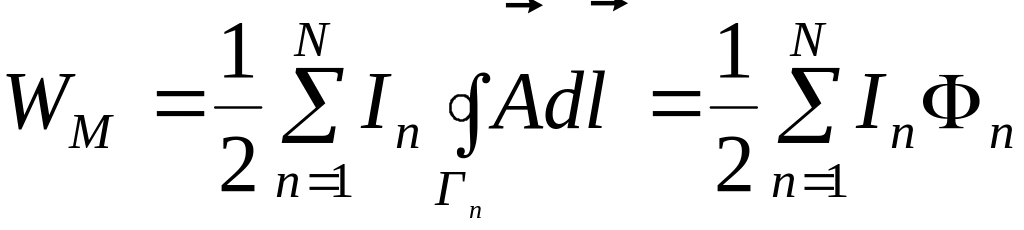. (17)

где — магнитный поток, сцепленный с контуром , а — ток в контуре .

В ф-ле (17) векторный потенциал и поток обусловлены не только током , но и токами в остальных контурах. В силу принципа суперпозиции можно записать следующее равенство:

, (18)

где — векторный потенциал, создаваемый в рассматриваемой точке током , протекающим в контуре .

Выделим в сумме (18) векторный потенциал , соответствующий току :

(19)

и подставим ф-лу (10) в (17). В результате получим

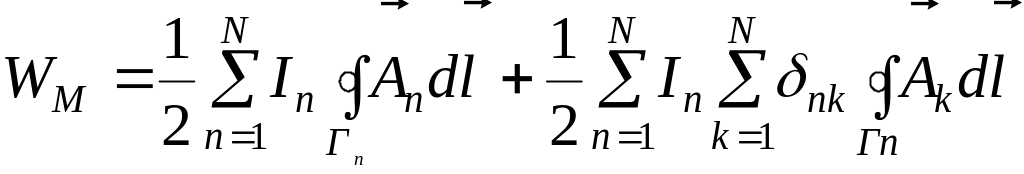
Преобразовав интегралы в полученном выражении с помощью теоремы Стокса, перепишем его в виде

, (20)

где — поток, сцепленный с контуром , который обусловлен током контура .

Первое слагаемое в правой части ф-лы (20) определяет собственную энергию контуров системы, а второе — взаимную энергию.

Индуктивность

Поток , пронизывающий уединенный контур Г, пропорционален току в этом контуре:

. (21)

Коэффициент зависит от конфигурации и размеров контура Г и называется его индуктивностью. Индуктивность измеряется в генри (Гн). Из закона индукции Фарадея и ф-лы (21) следует, что индуктивность уединенного контура численно равна величине эдс, наводимой в этом контуре при линейном изменении его тока на 1 А за 1 с. Подставляя ф-лу (21) в (16), получаем

. (22)

В случае контуров поток пропорционален току :

. (23)

Коэффициент пропорциональности при называют взаимной индуктивностью контуров и , а коэффициент — собственной индуктивностью контура .

Из закона индукции Фарадея и ф-лы (23) следует, что взаимная индуктивность двух контуров численно равна эдс, наводимой в одном из них при линейном изменении тока в другом на 1 А за 1 с.

Коэффициент при можно определить следующим образом. Воспользовавшись ф-лой (15) и выражением

,

представим выражение для потока в виде

, (24)

где и — элементы контуров и , a — расстояние между этими элементами.

Приравнивая правые части ф-л (24) и (23), получаем

. (25)

Из ф-лы (25) следует, что взаимная индуктивность контуров и зависит только от их формы и взаимного расположения и не изменяется при перестановке индексов (свойство взаимности):

. (26)

Для определения собственной индуктивности контура ф-ла (25) непригодна. Обычно вместо нее используют соотношения (21) и (22).

Преобразуем выражение для магнитной энергии системы линейных токов (20), подставив в него ф-лу (23):

.

Таким образом, для определения магнитной энергии системы линейных токов достаточно знать собственные и взаимные индуктивности контуров и токи в них.