Магнитостатика

Предположим, что в каждой точке рассматриваемой области плотность тока проводимости равна нулю , а сама область не охватывает тока. Уравнения группы (1а), описывающие магнитное поле, в этом случае не зависят от уравнений группы (1б) и переходят в уравнения магнитостатики

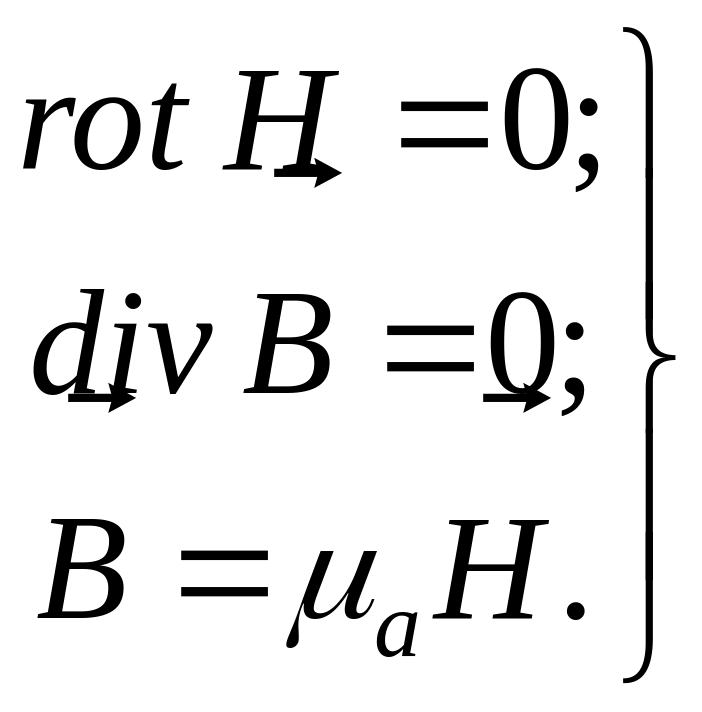. (4)

Интегральные соотношения магнитостатики получаются из уравнений (3), если в последних положить :

.

Так как в рассматриваемом случае , то по аналогии с электростатикой можно ввести в рассмотрение скалярную функцию , называемую магнитостатическим потенциалом и связанную с вектором соотношением

.

В однородной среде магнитостатический потенциал удовлетворяет уравнению Лапласа:

.

Разность значений магнитостатического потенциала между точками и можно (по аналогии с электростатикой) представить в форме

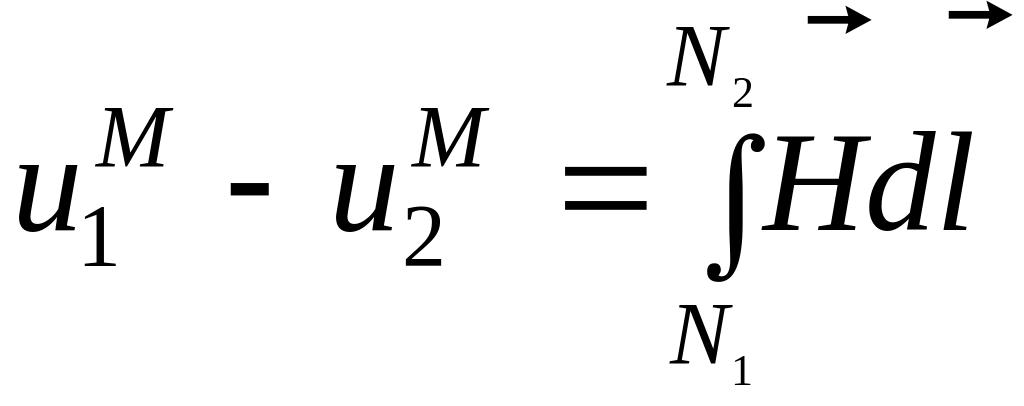. (5)

На границе раздела двух сред с разными магнитными проницаемостями ( ) должны выполняться общие граничные условия для векторов и :

;

.

Таким образом, напряженность магнитостатического поля и напряженность электростатического поля в области без зарядов удовлетворяют одинаковым уравнениям и однотипным граничным условиям. Следовательно, решение задач магнитостатики можно получить из решений аналогичных задач электростатики простой заменой в них на и на .

Магнитное поле и постоянный ток

В тех случаях, когда в рассматриваемой области имеется ток или область охватывает ток (рис. 2), магнитостатический потенциал становится неоднозначной функцией. Разность его значений между точками и зависит от контура, по которому выполняется интегрирование в ф-ле (5), а именно, при каждом обходе контура вокруг тока в положительном направлении (так, чтобы контур образовывал с током правовинтовую систему) значение интеграла в (5) возрастает на величину .

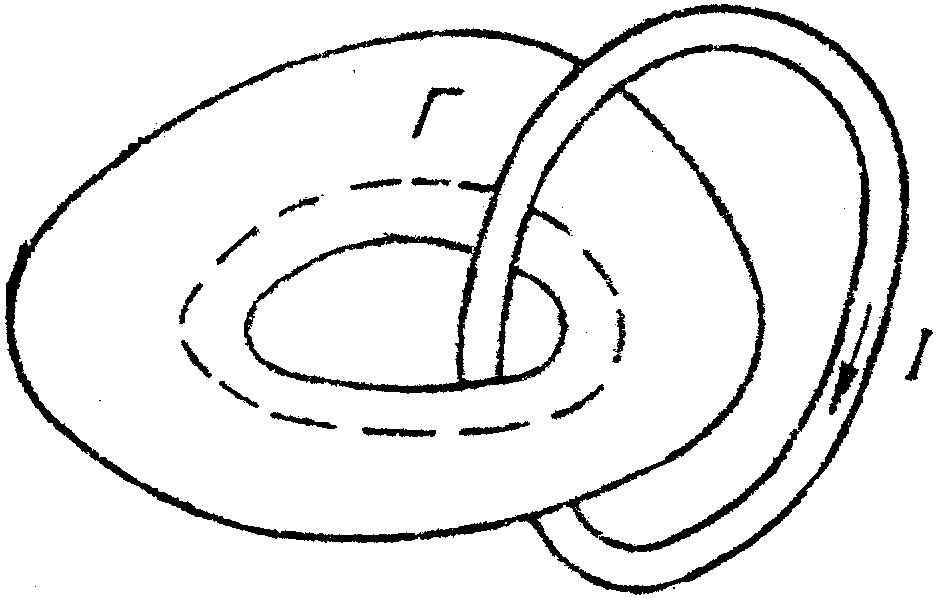
Рис. 2

Таким образом, магнитостатический потенциал не позволяет установить связь между стационарным магнитным полем и создающим его постоянным током. Для определения стационарного поля обычно вводят векторный потенциал , связанный с векторами и соотношениями

.

Основные формулы для вектора , характеризующего стационарное магнитное поле, можно получить непосредственно из формул для электродинамического потенциала , если считать все величины не зависящими от времени.

Векторный потенциал стационарного поля удовлетворяет уравнению

и условию калибровки

.

Если токи сосредоточены в ограниченной области , то:

.

где — расстояние от элемента до точки, в которой вычисляется потенциал.

Если токи распределены по поверхности с плотностью , то:

,

а в случае линейного тока , протекающего по контуру Г:

.

В последних двух ф-лах — расстояние от элементов и соответственно до точки, в которой вычисляется потенциал.

Перейдем от векторного потенциала к напряженности магнитного поля . Предполагая, что пространство заполнено однородной изотропной средой, получаем

.

Учитывая, что плотность тока не зависит от координат точки, в которой вычисляется поле, и используя тождество

,

преобразуем подынтегральное выражение:

,

где - орт вектора, проведенного из в точку наблюдения. Тогда получаем

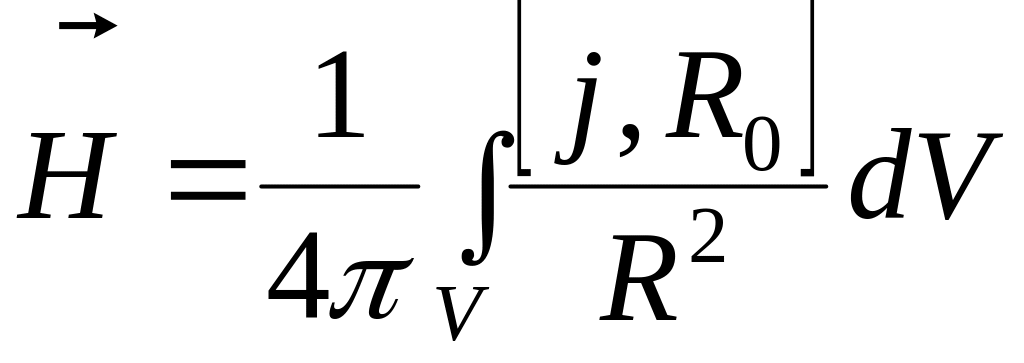. (6)

К аналогичным выражениям для вектора приходим в случае поверхностных и линейных токов:

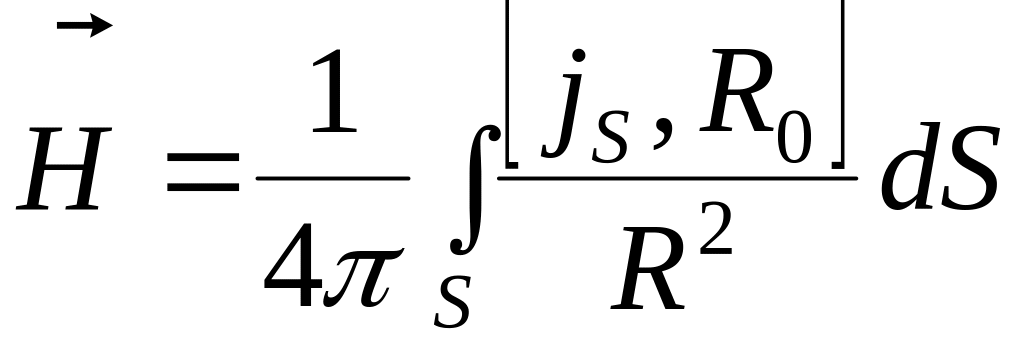; (7)

. (8)

Соотношения (6) … (8) представляют собой интегральные формы закона Био—Савара

. (9)

Закон Био—Савара характеризует магнитное поле , создаваемое элементом тока . Связь ф-л (8) и (9) очевидна. Покажем, что поля, определяемые выражениями (6) и (7), также можно представить в виде суперпозиции элементарных полей , определяемых соотношением (9), от отдельных «элементарных токов».

Преобразуем подынтегральное выражение в ф-ле (6). Выберем в качестве элемента элемент токовой трубки длиной , ось которой направлена по току, а сечение равно . Обозначив через полный ток, протекающий по трубке, и учитывая множитель перед интегралом, получим выражение

,

полностью совпадающее с правой частью ф-лы (9).

Связь формул (7) и (9) доказывается аналогично.

Часто при решении практических задач для упрощения расчета предполагается, что ток вдоль одной из координатных осей остается неизменным, т. е. что линии тока по этой координате уходят в бесконечность. Такие предположения обычно делаются при определении поля, создаваемого линейным током, который протекает вдоль длинной нити, или токами, протекающими вдоль длинного цилиндра. Рассмотрим эти особые случаи.

Найдем магнитное поле и векторный потенциал бесконечной уединенной нити, обтекаемой постоянным током. Пусть эта нить совпадает с осью цилиндрической системы координат. Очевидно, что напряженность магнитного поля в этом случае имеет одну составляющую и не зависит от переменных и . Выбирая в качестве контура Г в ф-ле (3) окружность радиуса , лежащую в плоскости, перпендикулярной к оси , получаем, что напряженность магнитного поля нити

.

За направление тока в этой ф-ле принято направление оси .

Векторный потенциал рассматриваемой нити должен иметь только -составляющую , величина которой зависит от координаты . Учитывая ф-лу

и расписывая в цилиндрической системе координат, получим

,

откуда следует, что

.

Интегрируя это выражение по , находим

.

Постоянную в этой ф-ле обычно полагают равной нулю. Тогда

.

От этой ф-лы нетрудно перейти к выражению для потенциала, создаваемого токами, неизменными вдоль оси , которые протекают по цилиндру произвольного сечения :

где — расстояние от элемента , характеризуемого координатами до точки наблюдения ; .

Если поле создано поверхностными токами, распределенными по некоторой цилиндрической поверхности , образующие которой параллельны оси , а плотность поверхностных токов не зависит от координаты , то векторный потенциал выражается формулой

где Г — линия пересечения поверхности с плоскостью, перпендикулярной к оси , a — расстояние от элемента до точки , в которой вычисляется потенциал.