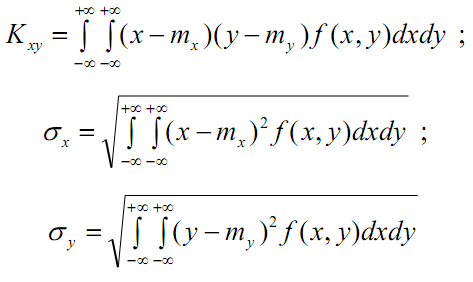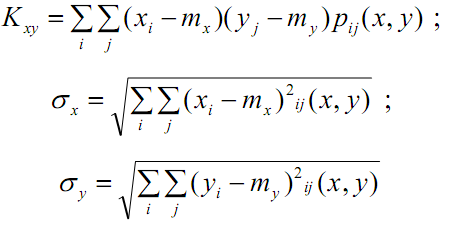Лабораторная работа №4 Определение статистических оценок многомерных случайных процессов.

1. Цель работы

Получить теоретические знания и практические навыки по определению статистических оценок многомерных случайных процессов на основе корелляционого анализа, а также по применению регрессии.

2. Общие сведения

2.1. Ковариация

Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация двух случайных величин (X,Y) характеризует не только степень зависимости случайных величин (ковариация двух независимых случайных величин равна нулю), но также их рассеивание вокруг точки  .

Это средство вычисляет ковариационную матрицу компонентов многомерной выборки. Диагональные элементы матрицы равны выборочным дисперсиям, а внедиагональные — ковариациям соответствующих компонентов. На рис.4.1 показана многомерная выборка, имеющая совместное нормальное распределение, причем первая пара компонентов зависима с коэффициентом корреляции 0,5. С таким же коэффициентом корреляции зависимы третий и четвертый компоненты выборки. Первая и вторая пары компонентов между собой независимы.

Внедиагональные элементы ковариационной матрицы рассчитываются по формулам: ковариация cov(X, Y) между компонентами х и у многомерной выборки вычисляется как

, где , , п — объем выборки.

Отметим, что эти же вычисления выполняет функция КОВАР. Диагональные элементы матрицы — выборочные дисперсии — вычисляются по стандартным формулам . Выборочную дисперсию также вычисляют функции ДИСПР и ДИСПРА.

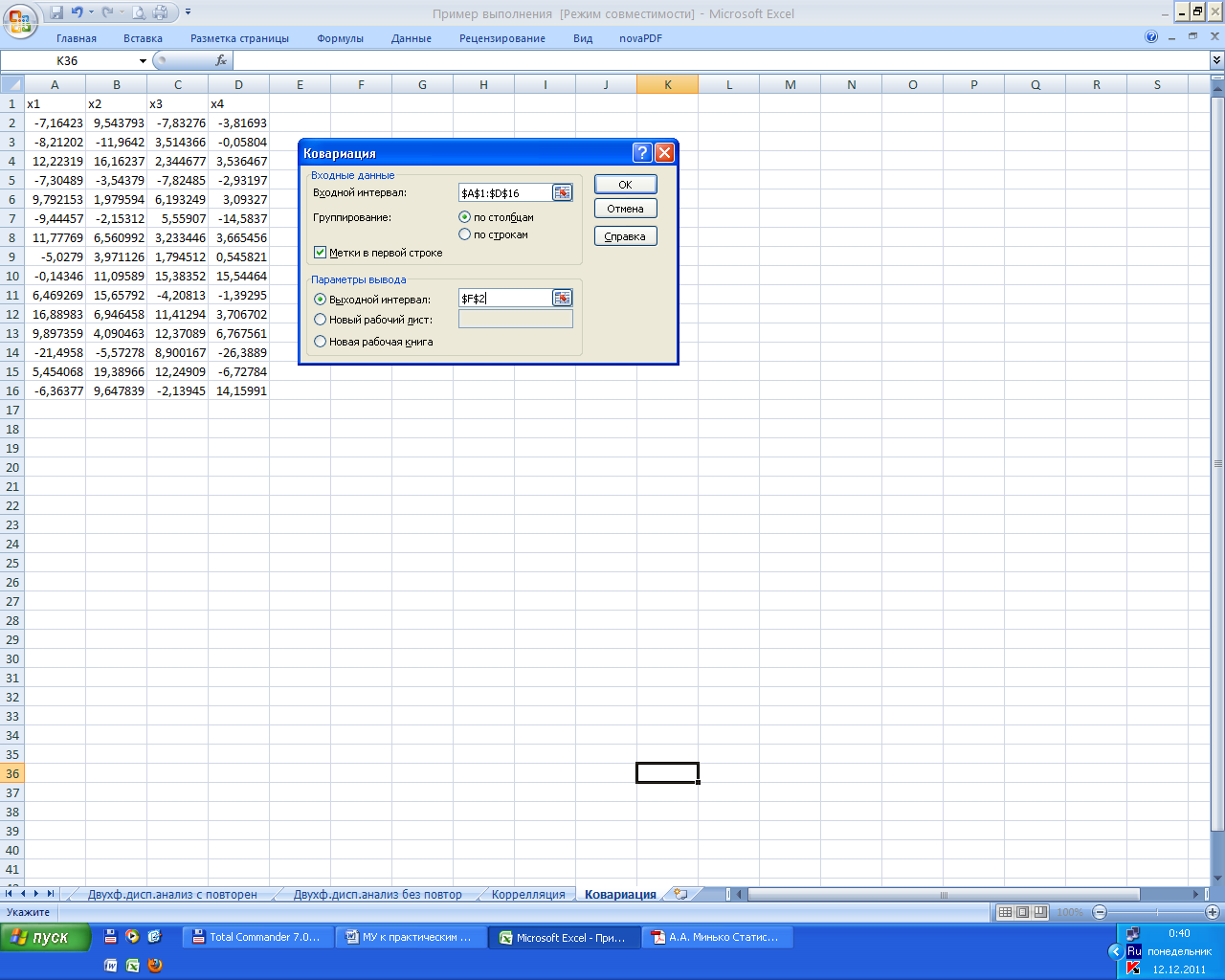
Рис. 4.1. Исходные данные и диалоговое окно Ковариация

На рис.4.2 показан результат применения средства Ковариация. Поскольку ковариационная матрица симметрична, выводится только нижняя ее половина.

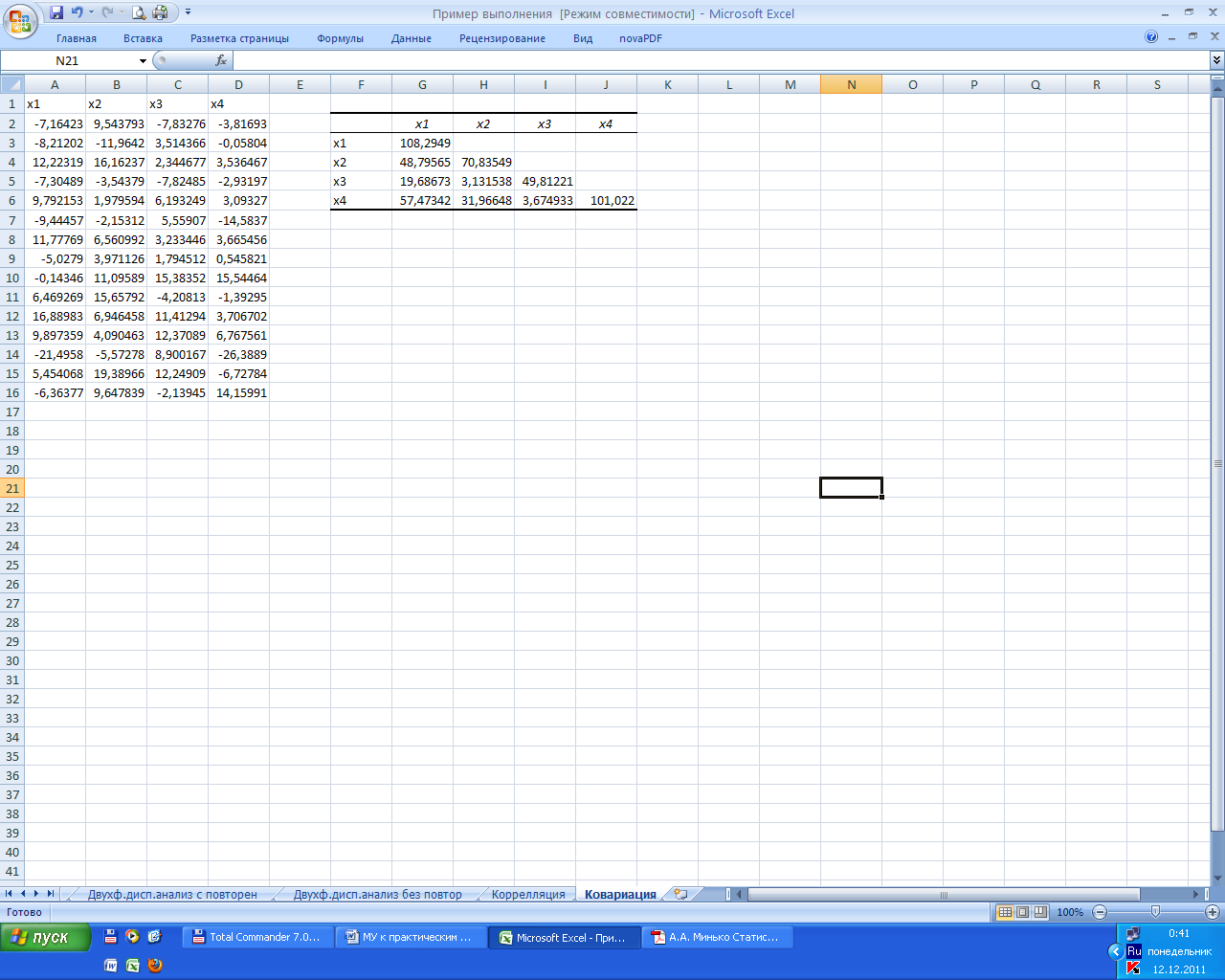
Рис. 4.2. Результат применения средства Ковариация

2.2. Корреляция

При построении корреляционных моделей исходят из условия нормальности многомерного закона распределения генеральной совокупности.

Значение коэффициента корреляции может изменяться в диапазоне от -1 до +1:

.

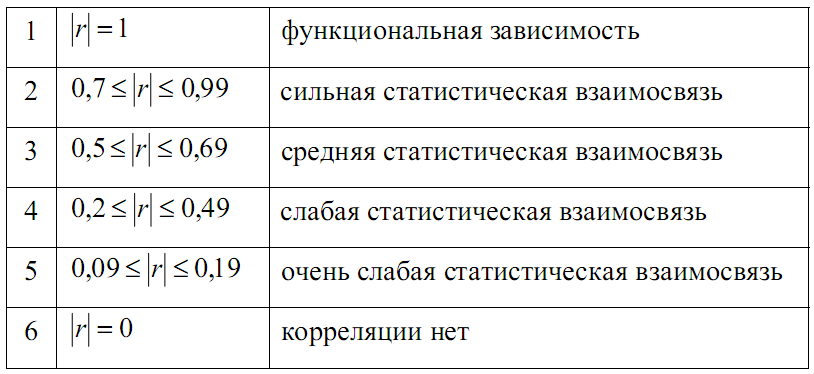
Абсолютное значение коэффициента корреляции показывает силу взаимосвязи. Чем меньше его абсолютное значение, тем слабее связь. Если он равен нулю, то связь вообще отсутствует. Чем больше значение модуля коэффициента корреляции, тем сильнее связь и тем меньше разброс в значениях y_i при каждом фиксированном значении x_i (таблица 1).

Таблица 1 – Интерпретация значений коэффициент корреляции

Знак коэффициента корреляции определяет направленность взаимосвязи: минус – отрицательная, плюс – положительная (см. рис. 4.3).

Рис.4.3. Корреляционные поля при различных значениях коэффициента корреляции

Коэффициент корреляции равен отношению корреляционного момента к произведению стандартных отклонений:

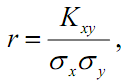
где

для непрерывных случайных величин	для дискретных случайных величин

В этих формулах m_x, m_y - математические ожидания случайных величин x и y, p_ij(x,y) – вероятность принятия случайными величинами x и y значений x_i и y_j, а f(x,y) – плотность распределения системы. Для дисперсий и корреляционного момента справедливы следующие оценки:

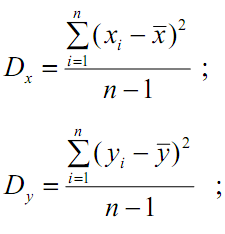
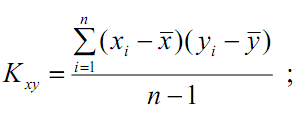
где и – средние, являющиеся оценками для соответствующих математических ожиданий. Поэтому формула для коэффициента корреляции может быть записана в виде

Либо

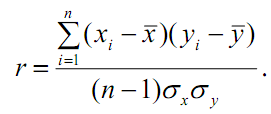
В ряде случаев тесноту взаимосвязи определяют на основании коэффициента детерминации. Коэффициент детерминации равен квадрату коэффициента корреляции, выраженному в процентах:

Коэффициент детерминации определяет, какая часть общей вариации одно показателя объясняется вариацией другого показателя, т.е. какая доля взаимосвязи между двумя наборами данных объясняется их взаимовлиянием. Остальная часть вариации обусловлена воздействием других неучтенных причин.

Средство Корреляция вычисляет корреляционную матрицу компонентов многомерной выборки. Диагональные элементы матрицы равны единице, а внедиагональные — коэффициентам корреляции соответствующих компонентов. На рис.4.4 показаны многомер­ная выборка, имеющая совместное нормальное распределение, причем первая пара компонентов зависима с коэффициентом корреляции 0,5. С таким же ко­эффициентом корреляции зависимы третий и четвертый компоненты выборки. Первая и вторая пара компонентов между собой независимы.

Рис.4.4. Исходные данные и диалоговое окно Корреляция

Внедиагональные элементы корреляционной матрицы рассчитываются по стандартным формулам: коэффициент корреляции между компонентами х и у многомерной выборки вычисляется как

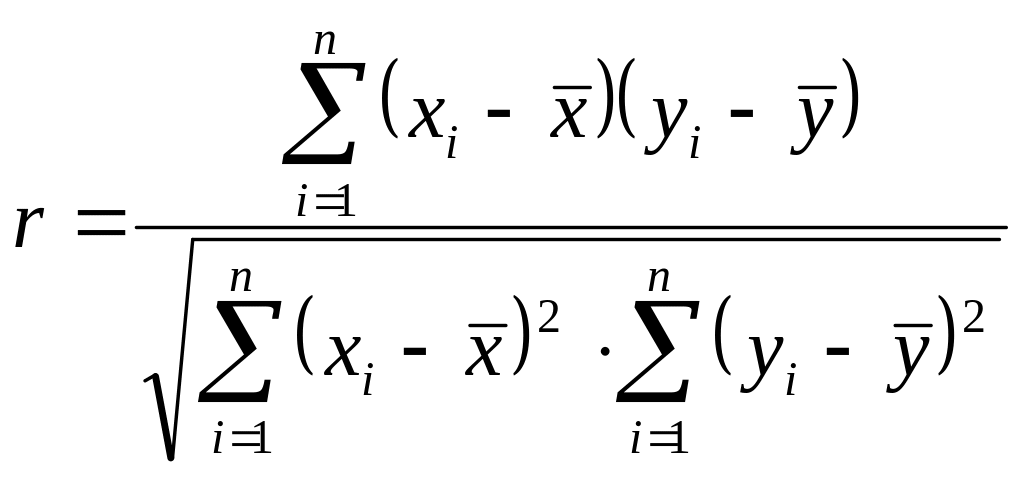, где , , п — объем выборки.

Отметим, что эти же вычисления выполняет функция КОРРЕЛ.

На рис. 4.5 показан результат применения средства Корреляция. Поскольку корреляционная матрица симметрична, выводится только нижняя ее половина.

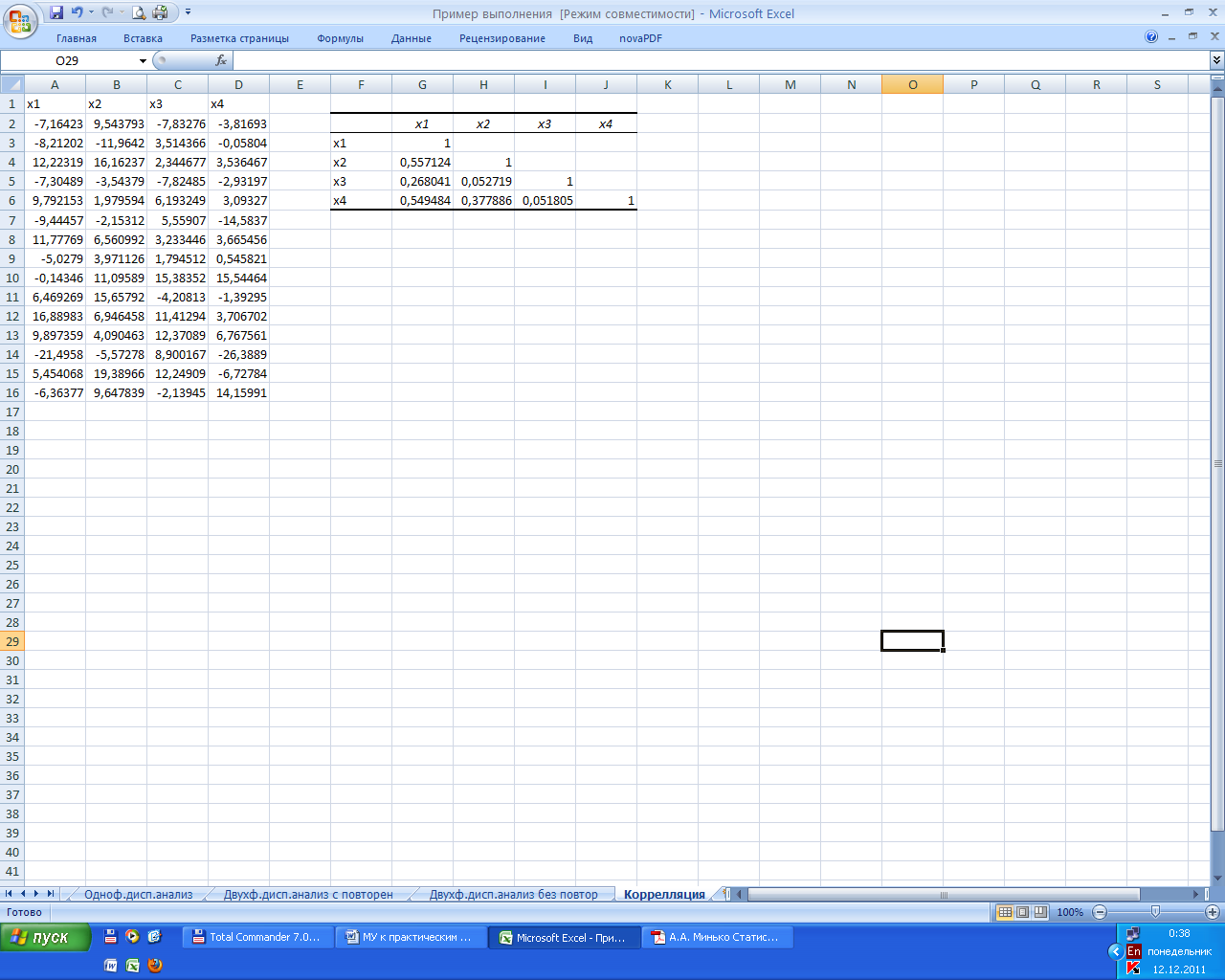
Рис. 4.5. Результат применения средства Корреляция