
- •3. Численные методы решения задач одномерной оптимизации унимодальных функций
- •3.1. Прямые методы. Предварительные сведения
- •3.2. Методы перебора и поразрядного поиска
- •3.3. Методы исключения отрезков
- •3.3.1. Метод деления отрезка пополам (дихотомии)
- •3.3.2. Метод золотого сечения
- •3.4. Метод парабол
- •4. Численные методы решения задач одномерной оптимизации многоэкстремальных функций
- •4.1. Метод ломаных
- •4.2. Метод покрытий
3. Численные методы решения задач одномерной оптимизации унимодальных функций
3.1. Прямые методы. Предварительные сведения
Для решения задачи минимизации функции f(x) на отрезке [а; b] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью в результате определения конечного числа значений функции f(x) в ее производных в некоторых точках отрезка [а; b]. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации. Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f(x) в заданных точках.
Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума.
Самым слабым требованием на функцию, позволяющим использовать эти методы, является ее унимодальность.
Функция
f(x)
называется унимодальной на отрезке [а;
b]
, если она непрерывна на [а;
b],
и существует два числа
![]() которые
которые
![]() такие, что:
такие, что:
если
 ,
то на отрезке
,
то на отрезке
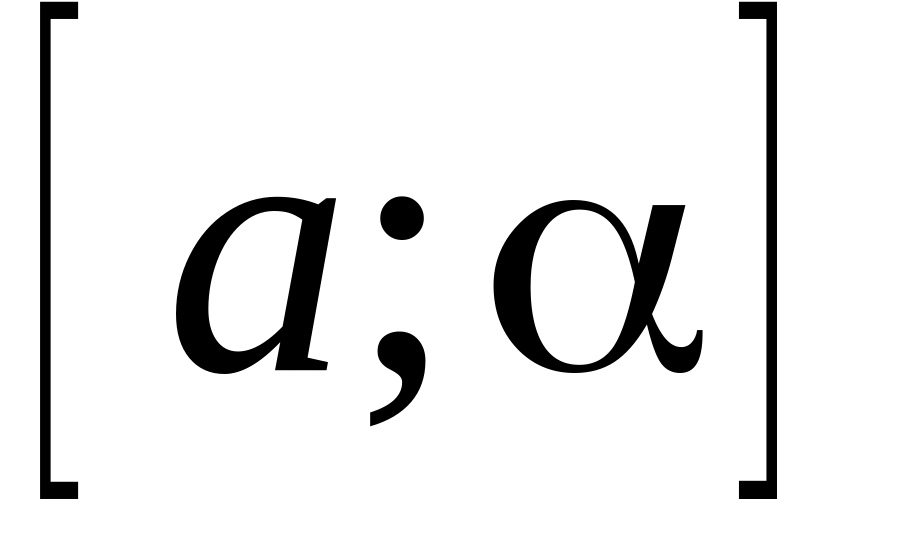 функция f(x)
монотонно убывает;
функция f(x)
монотонно убывает;если
 ,
то на отрезке
,
то на отрезке
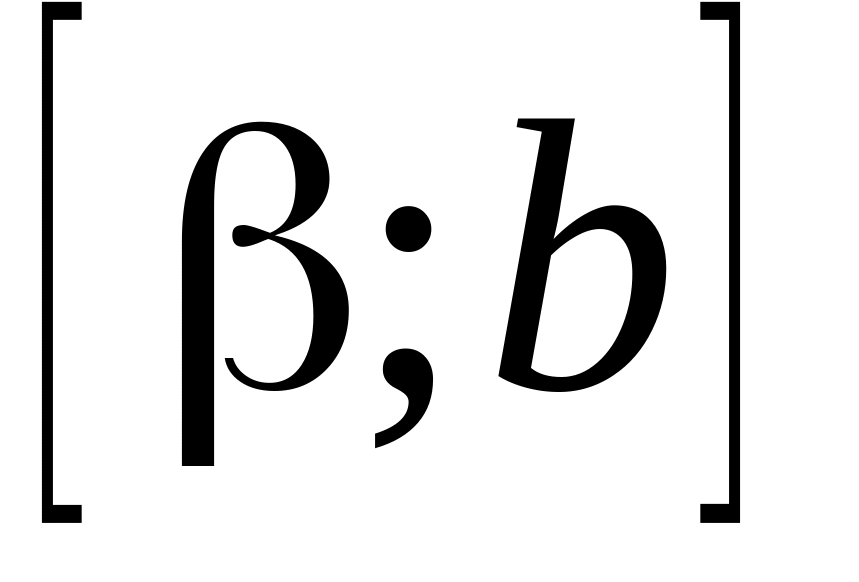 функция
f(x)
монотонно возрастает;
функция
f(x)
монотонно возрастает;если
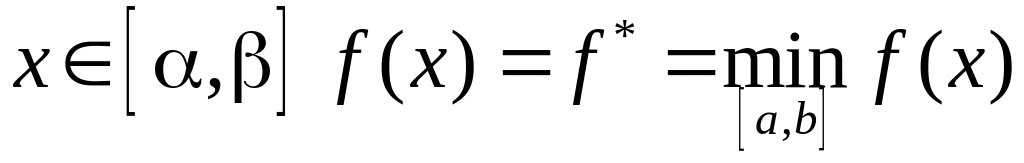
Применение некоторых методов одномерной минимизации возможно только в случае, если скорость изменения целевой функции на любом участке отрезка ограничена некоторым числом, одним и тем же для всех участков. В этом случае говорят, что данная функция удовлетворяет на этом участке условию Липшица. Целевые функции большинства практических задач оптимизации указанным свойством обладают.
Определение.
Функция f(x)удовлетворяет
на отрезке [а; b]
условию Липшица, если существует такое
число
![]() (константа Липшица), что
(константа Липшица), что
![]()
для
всех
![]() ,
принадлежащих [а; b].
,
принадлежащих [а; b].
3.2. Методы перебора и поразрядного поиска
Метод
перебора или равномерного поиска
является простейшим из прямых методов
минимизации и состоит в следующем.
Разобьем отрезок [а;
b]
на
![]() равных частей точками деления
равных частей точками деления
![]() .
Вычислив значения f(x)
в точках
.
Вычислив значения f(x)
в точках
![]() ,
путем сравнения найдем точку
,
путем сравнения найдем точку
![]() ,
для которой
,
для которой
![]()
Далее,
положим
![]()
Замечания:
1.
Погрешность определения точки минимума
![]() функции f(x)
методом перебора не превосходит
величины
функции f(x)
методом перебора не превосходит
величины
![]() .
.
2.
Пусть реализация метода перебора
потребовала N
вычислений функции f(x).
Это означает, что отрезок [а;
b]
был разбит на n
=N-1
частей и достигнутая точность определения
составила
![]() .
.
3.3. Методы исключения отрезков
В
методе перебора, рассмотрением выше,
точки
![]() в которых определяются значения
f(x),
выбираются заранее. Если же для выбора
очередной точки вычисления (измерения)
f(x)
использовать информацию, содержащуюся
в уже найденных значениях f(x),
то поиск точки минимума можно сделать
более эффективным, т.е. сократить число
определяемых для этого значений f(x),
как, например, в методе поразрядного
поиска. Один из путей такого более
эффективного поиска точки
в которых определяются значения
f(x),
выбираются заранее. Если же для выбора
очередной точки вычисления (измерения)
f(x)
использовать информацию, содержащуюся
в уже найденных значениях f(x),
то поиск точки минимума можно сделать
более эффективным, т.е. сократить число
определяемых для этого значений f(x),
как, например, в методе поразрядного
поиска. Один из путей такого более
эффективного поиска точки
![]() указывает свойство 3 унимодальных
функций. Пусть
указывает свойство 3 унимодальных
функций. Пусть
![]() .
Сравнив значения f(x)
в точках
.
Сравнив значения f(x)
в точках
![]() (пробных
точках), можно сократить отрезок поиска
точки
,перейдя
к отрезку
(пробных
точках), можно сократить отрезок поиска
точки
,перейдя
к отрезку
![]() ,
если
,
если
![]() или
к отрезку
или
к отрезку
![]() , если
, если
![]() (рис. 1). Описанную процедуру можно
повторить необходимое число раз,
последовательно уменьшая отрезок,
содержащий точку минимума. Когда
длина последнего из найденных отрезков
станет достаточно малой, следует положить
(рис. 1). Описанную процедуру можно
повторить необходимое число раз,
последовательно уменьшая отрезок,
содержащий точку минимума. Когда
длина последнего из найденных отрезков
станет достаточно малой, следует положить
![]() ,
где
,
где
![]() — одна из точек этого отрезка, например,
его середина. Методы минимизации,
основанные на этом принципе, называются
методами исключения отрезков.
— одна из точек этого отрезка, например,
его середина. Методы минимизации,
основанные на этом принципе, называются
методами исключения отрезков.
Чтобы относительное уменьшение отрезка на каждой итерации не зависело от того, какая из его частей исключается из дальнейшего рассмотрения, пробные точки следует располагать симметрично относительно середины исходного отрезка. В зависимости от способа выбора пробных точек получаются различные методы исключения отрезков. На практике используются следующие.
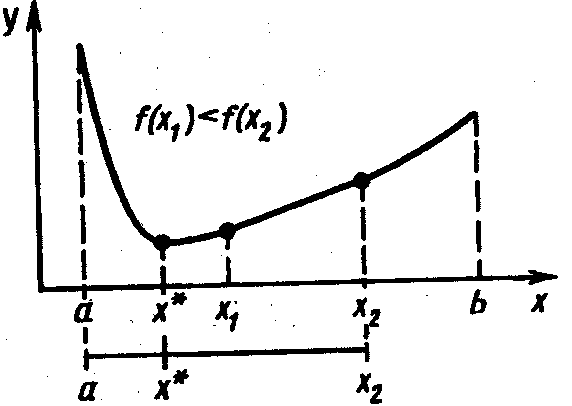
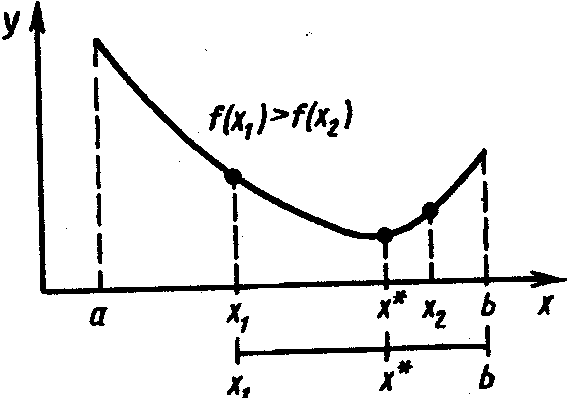
Рис. 1. Уменьшение отрезка поиска точки минимума методами исключения отрезков
