Словесная формулировка задачи

Требуется определить еженедельные затраты времени (в часах) на производство каждого из трех видов узлов на каждом заводе (переменные), не превышающие в сумме временные ресурсы каждого завода (ограничения) и обеспечивающие максимальный выпуск изделий (целевая функция)

Математическая формулировка

Пусть x_ij – недельный фонд времени (в часах), выделяемый на заводе i для производства узла j . тогда объемы производства каждого из трех комплектующих узлов будут равны:

узел 1: 8х₁₁ + 6х₂₁

узел 2: 5х₁₂ + 12х₂₂

узел 3: 10х₁₃ + 4х₂₃

Т.к. в конечной сборке каждый из комплектующих узлов представлен в одном экземпляре, количество конечных изделий должно быть равно количеству комплектующих узлов, объем производства которых минимален. Если, например, объем производства двух заводов составляет 100,112 и 108 соответствующих узлов, то количество конечных изделий будет равно min [100,112,108]=100. Поэтому количество конечных изделий можно выразить через число комплектующих узлов следующим образом:

min [8х₁₁ + 6х₂₁; 5х₁₂ + 12х₂₂; 10х₁₃ + 4х₂₃]

узел 1 узел 2 узел 3

Условия рассматриваемой задачи устанавливают ограничения только на фонд рабочего времени, которым располагает каждый завод. Таким образом, математическую модель можно представить в следующем виде:

Максимизировать z= min [8х₁₁ + 6х₂₁; 5х₁₂ + 12х₂₂; 10х₁₃ + 4х₂₃]

при ограничениях : х₁₁ + х₁₂ + х₁₃  100 (завод 1)

х₂₁ +х₂₂ +х₂₃  80 (завод 2)

x_ij  0, I=1,2; j=1,2,3

Эта модель не является линейной, но ее можно привести к линейной форме с помощью простого преобразования.

Пусть у – количество изделий = min [8х₁₁ + 6х₂₁; 5х₁₂ + 12х₂₂; 10х₁₃ + 4х₂₃]

Этому выражению с математической точки зрения эквивалента следующая формулировка:

Максимизировать у

при ограничениях: 8х₁₁ + 6х₂₁ у

5х₁₂ + 12х₂₂  у

10х₁₃ + 4х₂₃  у, где у 0 по определению.

Можно убиться в том, что максимизация у будет приводить к равенству этой переменной наименьшей из левых частей трех введенных ограничений, а это как раз и требуется.

Таким образом окончательно математическую модель можно записать в виде:

Максимизировать у

при ограничениях: 8х₁₁ + 6х₂₁- у  0

5х₁₂ + 12х₂₂ -у0

10х₁₃ + 4х₂₃ - у0

х₁₁ + х₁₂ + х₁₃  100

х₂₁ +х₂₂ +х₂₃  80

x_ij  0 для всех i и j, y0

Лекция 5:

Стандартная форма линейных оптимизационных моделей

Линейные оптимизационные модели можно решать с помощью графического и аналитического способов решения. Использование графического способа удобно только при решении задач ЛП с двумя переменными. При большем числе переменных необходимо применение аналитического аппарата. Рассмотрим общий метод решения задач ЛП, называемый симплекс – методом.

Информация, которую можно получить с помощью симплекс – метода, не ограничивается лишь оптимальными значениями переменных. Симплекс – метод фактически позволяет дать экономическую интерпретацию полученного решения и провести анализ модели на чувствительность.

Процесс решения задачи ЛП симплекс – методом носит итерационный характер: однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение. Процедуры, реализуемые в рамках симплекс – метода, требуют применения ЭВМ – мощного средства решения задач ЛП.

Симплекс – метод – это характерный пример итерационных вычислений, используемых при решении большинства оптимизационных задач.

Выше было показано, что правая и левая части ограничений линейной модели могут быть связаны знаками  , = и . Кроме того, переменные, фигурирующие в задачах ЛП, могут быть неотрицательными или не иметь ограничения в знаке. Для построения общего метода решения задач ЛП соответствующие модели должны быть представлены в некоторой форме, которую назовем стандартной формой линейных оптимизационных моделей. При стандартной форме линейной модели

1. все ограничения записываются в виде равенств с неотрицательной правой частью;

2. значения всех переменных модели неотрицательны;

3. целевая функция подлежит максимизации или минимизации.

Покажем, каким образом любую линейную модель можно привести к стандартной.

Ограничения

1. Исходное ограничение, записанное в виде неравенства типа  (), можно представить в виде равенства, прибавляя остаточную переменную к левой части ограничения (вычитая избыточную переменную из левой части).

Например, в левую часть исходного ограничения

х₁ + 2х₂  6 вводится остаточная переменная S₁>0, в результате чего исходное неравенство обращается в равенство

х₁ + 2х₂ + S₁=0 ; S₁0

Если исходное ограничение определяет расход некоторого ресурса, переменную S₁ следует интерпретировать как остаток, или неиспользованную часть, данного ресурса.

Рассмотрим исходное ограничение другого типа:

3х₁ + 2х₂ –3х₃  5

Т.к. левая часть этого ограничения не может быть меньше правой, для обращения исходного неравенства в равенство вычтем из его левой части избыточную переменную S₂ >0 . В результате получим

3х₁ + 2х₂ –3х₃- S₂=0 ; S₂0.

2. Правую часть равенства всегда можно сделать неотрицательной, умножая обе части –1.

Например, равенство 2х₁ +3х₂ –7х₃= -5 эквивалентно равенству

- 2х₁ -3х₂ + 7х₃= 5

3. Знак неравенства изменяется на противоположный при умножении обеих частей на –1.

Переменные

Любую переменную х_i , не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных:

x_i = x_i - x_i , где x_i, x_i  0.

Такую подстановку следует использовать во всех ограничениях, которые содержат исходную переменную х_i , а также и в выражении для целевой функции.

Обычно находят решение задачи ЛП, в котором фигурируют переменные x_i и x_i, а затем с помощью обратной подстановки определяют величину х_i. Важная особенность переменных x_i и x_i состоит в том, что при любом допустимом решении только одна из этих переменных может принимать положительное значение, т.е. если x_i>0, то x_i=0 и наоборот. Это позволяет рассматривать x_i как остаточную переменную, а x_i - как избыточную переменную, причем лишь одна из этих переменных может принимать положительное значение.

Целевая функция

Целевая функция линейной оптимизационной модели, представленной в стандартной форме, может подлежать как максимизации, так и минимизации. В некоторых случаях оказывается полезным изменить исходную целевую функцию.

Максимизация некоторой целевой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.

Например, максимизация функции z = 5x₁ + 2x₂ + 3x₃ эквивалента минимизации функции (-z) = -5x₁ - 2x₂ - 3x₃

Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных x₁ , x₂ и x₃ в обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны.

Лекция 6:

СИМПЛЕКС - МЕТОД . ПРЕДСТАВЛЕНИЕ ПРОСТРАНСТВА РЕШЕНИЙ СТАНДАРТНОЙ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАМИРОВАНИЯ

Симплекс – метод (СМ) не обладает той наглядность, которая характерна для геометрического представления пространства решений. В его вычислительной схеме реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Общую идею СМ можно проиллюстрировать на примере модели, построенной для задачи (краски). Пространство решений этой задачи представлено на рис.1. Исходной точкой алгоритма является начало координат (точка А на рис.1)

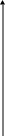
х_i Рис.1

E (4) D

(1)

(3) C

F (2)

A B x_e

Максимизировать Z= 3x_е + 2 x_i

при ограничениях x_е + 2 x_i  6 (1),

2x_е + x_i  8 (2),

-x_е + x_i  1 (3),

x_i  2 (4),

x_i  0 , x_е  0

Решение, соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке. В рассматриваемом случае это может быть либо точка В, либо точка F. Выбор точки зависит от коэффициентов целевой функции. Так как коэффициент целевой функции при x_e больше коэффициента при x_i , а целевая функция подлежит максимизации, требуемое направление перехода соответствует увеличению x_e , что приводит к экстремальной точке В. После этого указанный процесс повторяется, чтобы выяснить, существует ли другая экстремальная точка, соответствующая лучшему допустимому решению ( в данном случае большему значению целевой функции). Используя, как и ранее, информацию о целевой функции, можно определить, имеется ли на данном шаге алгоритма такая точка. В результате такой итеративный процесс позволяет найти оптимальную угловую точку С.

Выбор каждой последующей экстремальной точки при использовании СМ определяется следующими двумя правилами.

1. Каждая последующая угловая точка должна быть смежной с предыдущей. Например, в пространстве решений, изображенном на рис.1, невозможен прямой переход от точки А к точке С. Этот переход осуществляется по границам (ребрам) пространства решений: от точки А к точке В и лишь затем от точки В к точки С.

2. Обратный переход к предшествующей экстремальной точке не может производиться. Так, при движении в пространстве решений, представленном на рис.1, не должно быть обратного перехода от точки В к точке А.

Подводя итог изложению идей симплекс – метода, еще раз обратим внимание на то, что отыскание оптимального решения начинается с некоторой допустимой угловой точки, и все переходы осуществляются только к смежным точкам, причем перед новым переходом каждая из полученных точек проверяется на оптимальность. При решении задачи о красках начальным решением является точка А, из которой осуществляется переход в точку В и затем в точку С, соответствующую оптимуму. Таким образом, в данном случае для нахождения оптимального решения требуются три итерации ( получаемые решения изображаются точками А.В и С).

Чтобы описать рассмотренные процедуры формальными средствами, необходимо определить пространство решений и угловые точки алгебраически. Требуемые соотношения устанавливают из указанного в таблице соответствия геометрических и алгебраических определений.

Геометрическое определение (графический метод)	Алгебраическое определение (симплекс – метод)
Пространство решений	Ограничения модели стандартной формы (рис.1)
Угловые точки	Базисные решения задачи в стандартной форме

Представление пространства решений с помощью алгебраических методов рассмотрим на примере о красках. Соответствующая линейная модель, приведенная к стандартной форме, имеет следующий вид:

Maксимизировать Z= 3x_е + 2 x_i +0S₁ +0S₂ +0S₃ +0S₄

при ограничениях x_е + 2 x_i + S₁ = 6

2x_е + x_i +S₂ = 8

-x_е + x_i +S₃ = 1

x_i +S₄ = 2

x_i  0 , x_е  0 , S₁, S₂, S₃, S₄  0

На рис. 2 представлено пространство решений данной задачи. Каждую точку этого пространства можно определить с помощью переменных x_e, x_i, S₁, S₂, S₃ , S₄, фигурирующих в модели стандартной формы. Для идентификации нужной точки пространства решений воспользуемся тем, что при S_i=0, i=1,2,3,4, ограничения модели эквиваленты равенствам, которые представляются соответствующими ребрами пространства решений. Например, при S₁=0 первое ограничение задачи принимает вид равенства x_е + 2 x_i = 6, которое представляется ребром CD. Увеличение переменных S_i (S_i>0) будет соответствовать смещению допустимых точек с границ пространства решений в его внутреннюю область.

х_i Рис.2

G

E S₄=0 D K

S₁=0

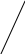
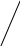S₃=0 C

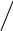F S₂=0

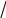x _e=0

A B x_e

x_i=0

Mинимизировать Z= 3x_е + 2 x_i

при ограничениях x_е + 2 x_i + S₁ = 6

2x_е + x_i +S₂ = 8

-x_е + x_i +S₃ = 1

x_i +S₄ = 2

x_i  0 , x_е  0 , S₁, S₂, S₃, S₄  0

Нас интересует прежде всего алгебраическое представление экстремальных точек. Анализируя рис.2, можно заметить, что переменные x_e, x_i, S₁, S₂, S₃ , S₄, ассоциированные с экстремальными точками А, В, С, D, E,F можно упорядочить, исходя из того, какое значение (нулевое или ненулевое) имеет данная переменная в экстремальной точке.

Анализируя таблицу, легко заметить две закономерности:

1. Стандартная модель содержит четыре уравнения и шесть неизвестных, поэтому в каждой из экстремальных точек две (=6-4) переменные должны иметь нулевые значения.

2. Смежные экстремальные точки отличаются только одной переменной в каждой группе (нулевых и ненулевых переменных).

Экстремальная точка	Нулевые переменные	Ненулевые переменные
A	xe, xi	S1,S2,S3,S4
B	S2, xi	S1,xe,S3,S4
C	S2, S1	xi,xe,S3,S4
D	S4, S1	xi,xe,S3,S2
E	S4, S3	xi,xe,S1,S2
F	S3, xe	xi,S4,S1,S2

Первая закономерность свидетельствует о возможности определения экстремальных точек алгебраическим способом путем приравнивания нулю такого количества переменных, которое равно разности между количеством неизвестных и числом уравнений. В этом состоит сущность свойства однозначности экстремальных точек. На рис.2 каждой неэкстремальной точке соответствует не более одной нулевой переменной. Так, любая точка внутренней области пространства решений вообще не имеет ни одной нулевой переменной, а любая неэктремальная точка, лежащая на границе, всегда имеет лишь одну нулевую переменную.

Свойство однозначности экстремальных точек позволяет определить их алгебраическим методом. Будем считать, что линейная модель стандартной формы содержит m уравнений и n ( m  n) не все допустимые экстремальные точки определяются как все однозначные неотрицательные решения системы m уравнений, в которых n – m переменных равны нулю.

Однозначные решения такой системы уравнений, получаемые путем приравнивания к нулю (n – m) переменных, называются базисными решениями. Если базисное решение удовлетворяет требованию неотрицательности правых частей, оно называется допустимым базисным решением. Переменные, имеющие нулевое значение, называются небазисными переменными, остальные – базисными переменными.

Из вышеизложенного следует, что при реализации СМ алгебраическое определение базисных решений соответствует идентификации экстремальных точек, осуществляемой при геометрическом представлении пространства решений. Таким образом, максимальное число итераций при использовании СМ равно максимальному числу базисных решений задачи ЛП, представленной в стандартной форме. Это означает, что количество итерационных процедур СМ не превышает

Cⁿ_m=n!/ [(n-m)!m!].

Вторая из ранее отмеченных закономерностей оказывается весьма полезной для построения вычислительных процедур СМ, при реализации которого осуществляется последовательный переход от одной экстремальной точки к другой, смежной с ней. Так как смежные экстремальные точки отличаются только одной переменной, можно определить каждую последующую (смежную) экстремальную точку путем замены одной из текущих небазисных (нулевых) переменных текущей базисной переменной. Таким образом, между множеством небазисных и множеством базисных переменных происходит взаимообмен переменными x_e и S₂ . Этот процесс можно наглядно представить в виде следующей таблицы.

Экстремальная точка	Небазисные (нулевые) переменные	Базисные переменные
A	xe, xi	S1,S2,S3,S4
B	S2, xi	S1,xe,S3,S4

Применяя аналогичную процедуру ко всем экстремальным точкам рис.2, можно убедиться в том, что любую последующую экстремальную точку всегда можно определить путем взаимной замены по одной переменной в составе базисных и небазисных переменных (предыдущей смежной точки). Этот фактор существенно упрощает реализацию вычислительных процедур СМ.

Рассмотренный процесс взаимной замены переменных приводит к необходимости введения двух новых терминов. Включаемой переменной называется небазисная в данный момент переменная, которая будет включена в множество базисных переменных на следующей итерации (при переходе к смежной экстремальной точке). Исключаемая переменная – это та базисная переменная, которая на следующей итерации подлежит исключению из множества базисных переменных.

Лекция 7:

ВЫЧИСЛИТЕЛЬНЫЕ ПРОЦЕДУРЫ СИМПЛЕКС – МЕТОДА

Симплекс – алгоритм состоит из следующих шагов.

Шаг 0 Используя линейную модель стандартной формы, определяют начальные допустимые базисные решения путем приравнивания к нулю n-m (небазисных) переменных.

Шаг 1 Из числа текущих небазисных (равных нулю) переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет, вычисления прекращаются, т.к. текущее базисное решение оптимально. В противном случае осуществляется переход к шагу 2.

Шаг 2 Из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое значение (стать небазисной) при введении в состав базисной новой переменной.

Шаг 3 Находится новое базисное решение, соответствующее новым составам небазисных и базисных переменных. Осуществляется переход к шагу 1.

Поясним процедуры СМ на примере решения нашей задачи. Сначало необходимо представить целевую функцию и ограничения модели в стандартной форме:

Z - 3x_е + 2 x_i =0 (целевая функция)

при ограничениях x_е + 2 x_i + S₁ = 6

2x_е + x_i +S₂ = 8

-x_е + x_i +S₃ = 1

x_i +S₄ = 2

x_i  0 , x_е  0 , S₁, S₂, S₃, S₄  0

Как отмечалось ранее, в качестве начального пробного решения используется решение системы уравнений, в которой две (6-4=2) переменные принимаются равными нулю. Это обеспечивает единственность и допустимость получаемого решения. В рассматриваемом случае очевидно, что подстановка x_e=x_i=0 сразу же приводит к следующему результату: S₁ =6, S₂ =8, S₃ =1, S₄ =2. Полученные результаты удобно представить в виде таблицы:

Базисные переменные	z	xe	xi	S1	S2	S3	S4	Решение
z	1	-3	-2	0	0	0	0	0 z - уравнение
S1	0	1	2	1	0	0	0	6 S1 - уравнение
S2	0	2	1	0	1	0	0	8 S2 - уравнение
S3	0	-1	1	0	0	1	0	1 S3 - уравнение
S4	0	0	1	0	0	0	1	2 S4 - уравнение

Эта таблица интерпретируется следующим образом. Столбец «Базисные переменные» содержит переменные пробного базиса S₁, S₂, S₃, S₄ значения которых приведены в столбце «Решение». При этом подразумевается, что небазисные переменные x_i и x_е (не представленные в первом столбце) равны нулю. Значение целевой функции z= 3х0+2х0+0х6+0х8+0х1+0х2 равно нулю, что и показано в последнем столбце таблицы.

Как определить, является ли полученное пробное решение наилучшим (оптимальным)? Анализируя z – уравнение, нетрудно заметить, что обе небазисные переменные x_i и x_е , равные нулю, имеют отрицательные коэффициенты. Это эквивалентно наличию положительных коэффициентов при этих переменных в исходной целевой функции. Так как мы имеем дело с задачей максимизации, значение z может быть улучшено при увеличении как x_е, так и x_i . Однако всегда выбирается переменная с большим абсолютным значением отрицательного коэффициента ( в z – уравнении ), т.к. практический опыт вычислений показывает, что в этом случае оптимум достигается быстрее.

Это правило составляет основу используемого в вычислительной схеме СМ условия оптимальности, которое состоит в том, что, если в задаче максимизации все небазисные переменные в z – уравнении имеют неотрицательные коэффициенты, полученное пробное решение является оптимальным. В противном случае в качестве новой базисной переменной следует выбрать ту, которая имеет наибольший по абсолютной величине отрицательный коэффициент.

Применяя условие оптимальности к исходной таблице, выберем в качестве переменной, включаемой в базис, переменную x_е. Исключаемая переменная должна быть выбрана из совокупности базисных переменных S₁, S₂, S₃, S₄. Процедура выбора исключаемой переменной предполагает проверку условия допустимости, требующего, чтобы в качестве исключаемой переменной выбиралась та из переменных текущего базиса, которая первой обращается в нуль при увеличении включаемой переменной x_е вплоть до значения, соответствующего смежной экстремальной точке. В рамках алгебраического представления каждая из таких точек пересечения определяется отношением постоянной правой части ограничения к соответствующему положительному коэффициенту при включаемой переменной. Интересующее нас отношение (фиксирующее искомую точку пересечения и идентифицирующее исключаемую переменную) можно определить непосредственно из симплекс – таблицы (С-Т).

Д ля этого в столбце, соответствующем вводимой переменной x_е , вычеркиваются отрицательные и нулевые элементы ограничений. Затем вычисляются отношения постоянных, фигурирующих в правых частях этих ограничений, к оставшимся элементам столбца, соответствующего вводимой переменной x_е . Исключаемой переменной будет та переменная текущего базиса, для которой указанное выше отношение минимально. Начальная С-Т для нашей задачи, получаемая после проверки условия допустимости (т.е. после вычисления соответствующих отношений и определения исключаемой переменной), воспроизводится ниже.

Базисные переменные	z	xe	xi	S1	S2	S3	S4	Решение Отношение
z	1	-3	-2	0	0	0	0	0
S1	0	1	2	1	0	0	0	6 6/1=6
S2	0	2	1	0	1	0	0	8 8/2=4
S3	0	- 1	1	0	0	1	0	1
S4	0	0	1	0	0	0	1	2

Для удобства описания вычислительных процедур, осуществляемых на следующей итерации, введем ряд необходимых определений.

Столбец С-Т, ассоциированный с вводимой переменной, будем называть ведущим столбцом.

Строку, соответствующую исключаемой переменной, назовем ведущей строкой (уравнением), а элемент таблицы, находящийся на пересечении ведущего столбца и ведущей строки, будем называть ведущим элементом.

После того как определены включаемая и исключаемая переменные (с использованием условий оптимальности и допустимости), следующая итерация (поиск нового базисного решения) осуществляется методом исключения переменных, или методом Гаусса – Жордана. Этот процесс изменения базиса включает вычислительные процедуры двух типов:

Тип1. (формирование ведущего уравнения).

Новая ведущая строка = предыдущая ведущая строка/ Ведущий элемент

Тип 2 (формирование всех остальных уравнений, включая z – уравнение)

Новое уравнение = Предыдущее уравнение – (коэффициент ведущего столбца предыдущего уравнения) х (Новая ведущая строка).

Выполнение процедуры типа 1 приводит к тому, что в новом ведущем уравнении ведущий элемент становится равным единице. В результате осуществления процедуры типа 2 все остальные коэффициенты, фигурирующие в ведущем столбце, становятся равными нулю. Это эквивалентно получению базисного решения путем исключения вводимой переменной из всех уравнений, кроме ведущего.

Применяя к исходной таблице процедуру типа 1, мы делим S₂ – уравнение на ведущий элемент, равный 2. Так как в столбце базисных переменных x_e занимает место переменной S₂, указанная процедура приводит к следующим изменениям исходной симплекс – таблицы:

Базисные переменные	z	xe	xi	S1	S2	S3	S4	Решение
z
S1
xe	0	1	1/2	0	1/2	0	0	8/2=4
S3
S4

Заметим, что в столбце «Решение» теперь фигурирует новое значение переменной x_e =4, которое равно минимальной величине отношений, анализируемых при проверке условия допустимости.

Чтобы составить новую симплекс – таблицу выполним необходимые вычислительные процедуры типа 2.

1 . Z – уравнение. Предыдущие z- уравнение: (1 –3 –2 0 0 0 0 0 )

- (-3) Новая ведущая строка: (0 3 3/2 0 3/2 0 0 12)

=Новое z - уравнение: (1 0 –1/2 0 3/2 0 0 12)

2. S₁-уравнение

П редыдущее S₁-уравнение: ( 0 1 2 1 0 0 0 6 )

- (1)х Новая ведущая строка: ( 0 -1 -1/2 0 -1/2 0 0 -4 )

= Новое S₁- уравнение: ( 0 0 3/2 1 –1/2 0 0 2 )

3. S₃- уравнение.

П редыдущее S₃- уравнение: ( 0 -1 1 0 0 1 0 1 )

-(-1)х Новая ведущая строка: ( 0 1 ½ 0 ½ 0 0 4 )

= Новое S₃- уравнение: ( 0 0 3/2 0 ½ 1 0 5 )

4. S₄- уравнение. Новое S₄- уравнение будет таким же, как и предыдущее, поскольку соответствует коэффициент ведущего столбца равен нулю.

Новая симплекс – таблица, полученная с помощью рассмотренных операций, имеет следующий вид:

Базисные переменные	Z	X E	Xi	S1	S2	S3	S4	Решение
Z	1	0	-1/2	0	3/2	0	0	12
S 1	0	0	3 /2	1	- 1/2	0	0	2 2/(3/2)=4/3
XE	0	1	1 /2	0	1/2	0	0	4 4/(1/2)=8
S3	0	0	3 /2	0	1/2	1	0	5 5/(3/2)=10/3
S4	0	0	1	0	0	0	1	2 2/1=2

В новом решении Х_Е = 4 и Х₁ = 0 (т.В на рис. 2). Значение Z возросло с 0 до 12. Это увеличение обусловлено тем, что прирост Х_Е на единицу обеспечивает увеличение Z на 3 единицы: таким образом, прирост целевой функции Z составляет 3 х 4 = 12.

Заметим, что новая симплекс – таблица обладает такими же характеристиками, как и предыдущая: только небазисные переменные Х₁ и S₂ равны нулю, а значение базисных переменных, как и раньше, представлены в столбце «Решение». Это в точности соответствует результатам, получаемым при использовании метода Гаусса – Жордана.

Из последней таблицы следует, что на очередной итерации в соответствии с условием оптимальности в качестве вводимой переменной следует выбрать Х₁, так как коэффициент при этой переменной в Z- уравнении равен – ½.

Исходя из условия допустимости, определяем, что исключаемой переменной будет S₁. Отношения, фигурирующие в правой части таблицы, показывают, что в новом базисном решении значение включаемой переменной Х₁ будет равен 4/3( = min отношению). Это приводит к увеличению целевой функции на (4/3) х (1/2) = 2/3.

К получению симплекс – таблицы, соответствующий новой итерации, приводят следующие вычислительные операции метода Гаусса – Жордана.

1. Новое ведущее (Х₁) – уравнение = Предыдущее S₁ – уравнение /(3/2).

2. Новое Z – уравнение = предыдущее Z – уравнение – (-1/2) х новое ведущее уравнение.

3. Новое Х_Е – уравнение = предыдущее Х_Е – уравнение – (1/2) х новое ведущее уравнение.

4. Новое S₃ – уравнение = предыдущее S₃ – уравнение – (3/2) х новое ведущее уравнение.

5. Новое S₄ – уравнение = предыдущее S₄ – уравнение –(1) х новое ведущее уравнение.

В результате указанных преобразований получим следующую симплекс – таблицу.

Базисные переменные	z	xe	xi	S1	S2	S3	S4	Решение
z	1	0	0	1/3	4/3	0	0	12 х 2/3
Хi	0	0	1	2/3	-1/3	0	0	4/3
хе	0	1	0	-1/3	2/3	0	0	10/3
S3	0	0	0	-1	1	1	0	3
S4	0	0	0	-2/3	1/3	0	1	2/3

В новом базисном решении Х_Е = 3 х 1/3 и Х₁ = 1 х 1/3 (точка С на рис. 2) Значение Z увеличилось с 12 (предыдущий симплекс – таблица) до 12 х 2/3. Этот результирующий прирост целевой функции ( 12 х 2/3 – 12) = 2/3 обусловлен увеличением Х₁ от 0 до 4/3, так как из Z- строки предыдущий симплекс – таблицы следует, что возрастанию данной переменной на единицу соответствует увеличение целевой функции на ½.

Последняя симплекс – таблица соответствует оптимальному решению задачи, так как в Z – уравнение ни одна из небазисных переменных не фигурирует с отрицательным коэффициентом. Получением этой результирующей таблицы и завершаются вычислительные процедуры симплекс – метода.

В рассмотренном выше примере алгоритм симплекс – метода использован при решении задачи, в которой целевая функция подлежала max. В случае min целевой функции в этом алгоритме необходимо изменить только условие оптимальности, то есть в качестве новой базисной переменной следует выбирать ту переменную, которая в Z - уравнении имеет наибольший положительный коэффициент. Условия допустимости в обоих случаях (max и min) одинаковы. Представляется целесообразным дать теперь окончательные формулировки обоим условиям, используемым в симплекс – методе.

Условие оптимальности. Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая в Z – уравнении наибольший отрицательный (положительный) коэффициент. В случае равенства таких коэффициентов для нескольких небазисных переменных выбор делается произвольно. Если все коэффициенты при небазисных переменных в Z – уравнении неотрицательны (неположительны), полученное решение является оптимальным.

Условие допустимости. В задачах максимизации и минимизации в качестве исключаемой переменной выбирается та базисная переменная, для которой отношение постоянной в правой части соответствующих ограничений к (положительным) коэффициентам ведущего столбца минимальны. В случае равенства этого отношения для нескольких базисных переменных выбор делается произвольно.

Упражнения.

1. Предположим, что при использовании симплекс – метода в задаче на отыскание максимума в качестве включаемой в базис переменной выбирается любая из небазисных, имеющих отрицательный коэффициент в Z – уравнении. Приведут ли в этом случае итерации симплекс – метода получению оптимального решения?

Ответ: Да, так как наличие отрицательного коэффициента при небазисных переменных в Z – уравнении указывает на возможность увеличения Z при возрастании значений этих переменных (в положительной области). Единственное преимущество выбора небазисной переменной с наибольшим по абсолютной величине отрицательным коэффициентом в Z – уравнении состоит в том, что такой выбор обеспечивает получение оптимального решения при минимальном числе итераций.

2. Воспользуйтесь графическим методом решения для задачи фирмы Reddy Mikks (рис. 2). Пусть начальному решению соответствует т. А, причем Х₁ представляет собой переменную, включаемую в базис на следующий итерации. Определите отношения, используемые при проверке условия допустимости, непосредственно из графика. Сравните полученные результаты с данными исходной симплекс – таблицы. Какая переменная подлежит исключению из базиса?

Ответ: Отношения (координаты точки пересечения с осью Х₁) равны 3, 8, 1 и 2. Исключению из базиса подлежит переменная S₃.

3. Применительно к условиям з. №2 определите увеличение целевой функции в базис переменной Х₁, не пользуясь методом Гаусса – Жордана.

Ответ: (увеличение Z = 2 х 1 = 2

4. Используя рис. 2 определите, сколько итераций потребуется для нахождения оптимального решения (т. С), если в исходной С-Т в качестве вводимой в базис переменной будет выбрана Х₁.

Ответ: Пять итераций, соответствуют экстремальным т. А, F, E, D и C.

5. Используя таблицу, содержащую оптимальное решение задачи фирмы Reddy Mikks, определите исключаемую переменную в соответствии изменение величины Z ( увеличение или уменьшение), если в качестве новой базисной переменной будет выбрана

а) S₁ ( Ответ: Исключению подлежит Х₁ при этом Z уменьшается на 2х1/2=2/3)

б) S₂ (Ответ: Исключению подлежит S₄ при этом Z уменьшается на 2х4/3=8/3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ ТАТАРСТАН

АЛЬМЕТЬЕВСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ИНСТИТУТ

Е.И. Егорова

Математическое моделирование

курс лекций

АЛЬМЕТЬЕВСК 2009

УДК 621.09.06(076)

Е.И. Егорова

Математическое моделирование: Курс лекций по дисциплине «Математическое моделирование» для студентов специальности 151001 «Технология машиностроения» всех форм обучения. – Альметьевск: Альметьевский государственный нефтяной институт, 2009.-42с.

В курсе лекций изложены: исследование операций как наука и искусство. Искусство моделирования. Предварительная классификация моделей исследования операций. Построение математической модели для задачи линейного программирования. Построение математических моделей. Стандартная форма линейных оптимизационных моделей. Приведение линейной формы математической модели к стандартному виду. Понятие остаточных и избыточных переменных. Симплекс – метод. Искусственное начальное решение. Интерпретация симплекс – таблиц. Анализ модели на чувствительность. Линейное программирование: двойственность. Транспортная модель. Решение транспортной задачи.

Рекомендуется для студентов высших учебных заведений, обучающихся по направлению 151000 «Конструкторско – технологическое обеспечение машиностроительных производств» для специальности 151001 «Технология машиностроения»

Лекция 8:

ИСКУССТВЕННОЕ НАЧАЛЬНОЕ РЕШЕНИЕ. М – метод (МЕТОД БОЛЬШИХ ШТРАФОВ). ДВУХЭТАПНЫЙ МЕТОД

Искусственное начальное решение.

В рассмотренной вычислительной схеме СМ для получения начального базисного решения использовались остаточные переменные. Однако, когда исходное ограничение записано в виде равенства или имеет знак , нельзя сразу же получить допустимое начальное базисное решение. Покажем это на следующем примере:

минимизировать Z = 4x₁ + x₂

при ограничениях 3х₁ + х₂=3 х₁, х₂  0

4х₁ +3х₂  6

х₁ + 2х₂  4

Чтобы записать задачу в стандартной форме, введем в левую часть ограничения (2) избыточную х₃, а в левую часть ограничения (3) – остаточную переменную х₄. В результате получим следующую формулировку задачи:

минимизировать Z = 4х₁ + х₂

при ограничениях 3х₁ + х₂ = 3

4х₁ + 3х₂ – х₃ = 6

х₁ + 2х₂ + х₄ = 4

х₁; х₂; х₃; х₄  0

Таким образом, имеются 3 уравнения, содержащие 4 независимых. Это означает, что каждому базисному решению соответствует одна небазисная переменная (равная нулю). В отличие от случая, когда каждое уравнение содержит остаточную переменную, в данной ситуации уже нельзя быть уверенным в том, что при нулевом значении одной из переменных все базисные переменные будут не отрицательными. При выборе переменной, которой следует приписать нулевое значение, можно, конечно, использовать метод проб и ошибок. Однако этот метод требует дополнительных затрат времени и неудобен для выполнения расчетов на ЭВМ. Поэтому следует применить более рациональный способ нахождения начального допустимого базисного решения.

Идея использования искусственных переменных достаточна проста. Она предполагает включения неотрицательных переменных в левую часть каждого из уравнений, не содержащих « очевидных» начальных базисных переменных. Обеспечивая получение начального базиса, эти дополнительно вводимые переменные выполняют, по существу, ту же роль, что и остаточные переменные. Однако, поскольку такие искусственные переменные не имеют отношения к содержанию поставленной задачи (отсюда и их название « искусственное»), их введение допустимо только в том случае, если соответствует схема вычислений будет обеспечивать получение оптимального решения, в котором все искусственные переменные окажутся = 0. Другими словами, эти переменные следует использовать только для получения «стартовой» точки, причем итеративный процесс оптимизации должен «вынуждать» эти переменные принимать нулевые значения в конечном оптимальном решении, обеспечивая допустимость оптимума.

Добиться желаемого результата позволяет использование в итерационном процессе обратной связи, обеспечивающий в конечном итоге получение оптимального решения при нулевых значениях искусственных переменных (при условии, что допустимое оптимальное решение задачи существует.) Для построения требуемой схемы вычислений можно применить следующий прием: наложить «штраф» за использование искусственных переменных, вводимых в целевую функцию. Разработаны два (тесно связанных между собой) метода получения стартовой точки, в которых используется «штрафование» искусственных переменных:

1. М-метод, или метод больших штрафов.

2. Метод, предусматривающий решение исходной задачи в два этапа (двухэтапный метод.)

Рассмотрим М – метод на примере сформулированной выше задачи.

М – метод (метод больших штрафов).

Рассмотрим введенную ранее линейную модель, приведенную к стандартной форме:

минимизировать: Z = 4х₁ + х₂

при ограничениях: 3х₁ + х₂ = 3

4х₁ + 3х₂ – х₃ = 6

х₁ + 2х₂ + х₄ = 4

х₁; х₂; х₃; х₄  0

В (1) и (2) уравнениях нет переменных, выполняющих роль остаточных. Поэтому введем в каждое из этих уравнений по одной искусственной переменной, обозначив их через R₁ и R₂:

3х₁ + х₂ + R₁ = 3

4x₁ + 3x₂ – x₃ + R₂ = 6

За использование этих переменных в составе целевой функции можно ввести штраф, приписывая или достаточно большой положительный М. Такой способ введения искусственных переменных R₁ и R₂ приводит к следующей линейной модели:

Минимизировать Z = 4х₁ + х₂ + МR₁ + MR₂

При ограничениях 3х₁ + х₂ + R₁ = 3

4x₁ + 3x₂ – x₃ + R₂ = 6

x₁ + 2x₂ + x₄ = 4

x₁; x₂; x₃; x₄; R₁; R₂  0

Обратим внимание на логику использования искусственных переменных. Имеются три уравнения и 6 неизвестных. Следовательно, начальное базисное решение должно включить 6 – 3 =3 нулевые переменные. Если положить = 0 переменные х₁; х₂; х₃, то сразу же будет получено требуемое начальное допустимое решение:

R₁ = 3 R₂ = 6 и х₄ = 4.

Рассмотрим теперь, каким образом «новая» структура модели автоматически приводит к тому, что на конечной стадии процесса оптимизации переменные R₁и R₂ принимают нулевое значение. Так как мы имеем дело с задачей на отыскание минимума, а переменные R₁ и R₂ в целевой функции приписан большой по величине положительный коэффициент М, то метод оптимизации, направленный на нахождение минимального значения Z, приведет к тому, что переменные R₁ и R₂ в оптимальном решении обратятся в нуль. Заметим, что все промежуточные итерации, предшествующие получению оптимума, не имеют значения с точки зрения окончательного результата. Поэтому не важно, фигурируют ли на этих итерациях положительные искусственные переменные.

Как следует видоизменить М – метод, если целевая функция подлежит не минимизации, а максимизации? Используя тот же самый прием штрафования искусственных переменных, следует приписать этим переменным в целевой функции достаточно большой по абсолютной величине отрицательный коэффициент –М (М > 0), что обусловит недопустимость положительных значений искусственных переменных в оптимальном решении.

Пример: Положим, что в рассматриваемом примере поставлена задача на отыскание максимума какой вид будет иметь целевая функция модели после введения искусственных переменных?

Ответ: Максимизировать Z = 4х₁ + х₂ – МR₁ – MR₂

После получения допустимого начального решения нужно так «переформулировать» условия задачи, чтобы можно было представить процесс решения в удобной табличной форме. Для этого необходимо, чтобы начальное решение в явном виде фигурировало в столбце, характеризуем правые части всех уравнений модели. Этого можно добиться, представляя в целевую функцию полученные из соответствующих ограничений выражения для искусственных переменных.

R₁ = 3 – 3x₁ – x₂

R₂ = 6 – 4x₁ – 3x₂ + x₃

В результате получается следующие выражения для Z:

Z = 4х₁ + х₂ + М(3 – 3х₁ – х₂) + М(6 – 4х₁- 3х₂ + х₃) = (4 – 7М)х₁ + (1 – 4М)х₂ – Мх₃ + 9М

При этом Z – уравнение в С-Т будет иметь вид:

Z – (4 – 7М)х₁ – (1 –4М)х₂ – Мх₃ = 9М

Таким образом, стартовой точке, в которой х₁ = х_{2 =} х₃ = 0, соответствует значение Z = 9М, как это и должно быть при R₁ = 3 и R₂ = 6.

Последовательность С-Т, приводящих к оптимальному решению задачи. Так как целевая функция минимиз. Переменные, включаемые в базис, должны иметь наибольшие положительные коэффициенты в Z – уравнении. Оптимум достигается в той итерации, где все небазисные переменные имеют неположительный коэффициент в Z – уравнении.

№1а. минимизировать: Z = 4х₁ + х₂

при ограничениях: 3х₁ + х₂ = 3

4х₁ + 3х₂  6

х₁ + 2х₂  4

х₁; х₂  0

минимизировать: Z = 4х₁ + х₂

при ограничениях: 3х₁ + х₂ = 3

4х₁ + 3х₂ – х₃ = 6

х₁ + 2х₂ – х₄ = 4

х₁; х₂; х₃; х₄  0

минимизировать: Z = 4х₁ + х₂ + MR₁ + MR₂ +MR₃

при ограничениях: 3х₁ + х₂ + R₁ = 3

4x₁ + 3x₂ – x₃ + R₂ = 6

x₁ + 2x₂ – x₄ + R₃ = 4.

R₁ = 3 – 3x₁ – x₂

R₂ = 6 – 4x₁ – 3x₂ + x₃

R₃ = 8 – x₁ – 2x₂ + x₄

Z = 4x₁ + x₂ + M(3 – 3x₁ – x₂) + M(6 – 4x₁ – 3x₂ + x₃) + M(4 – x₁ – 2x₂ + x₄) =

= 4x₁ + x₂ + 3M - 3x₁M - x₂M + 6M - 4x₁M - 3x₂M + x₃M + 4M – x₁M –2x₂M +

+ x₄M = 4x₁ + x₂ - M(8x₁ -6x₂ +x₃ +x₄) + 17M = 4x₁ + x₂ + 17M - 8x₁M - 6x₂M+

+x₃M + x₄M = (4 – 8M)x₁ + (1 - 6M)x₂ + x₃M + x₄M +13M;

Z - (- 4 + 8M)x₁ - (-1 + 6M)x₂ – x₃M – x₄M = 13M.

б) минимизировать: Z = 4x₁ + x₂

при ограничениях: 3x₁ +x₂ = 3

4x₁ + 3x₂  6 x₁; x₂  0.

X₁ + 2x₂  4

минимизировать: Z = 4x₁ + x₂

при ограничениях: 3x₁ + x₂ = 3

4x₁ + 3x₂ + x₃ = 6 x₄; x₁; x₂; x₃  0

x₁ + 2x₂ + x₄ = 4

минимизировать: Z = 4x₁ + x₂ + MR₁

при ограничениях: 3x₁ + x₂ +R₁ = 3

4x₁ + 3x₂ + x₃ = 6

x₁ + 2x₂ + x₄ = 4

R₁ = 3 – 3x₁ – x₂

Z = 4x₁ + x₂ + M(3 – 3x₁ – x₂) = 4x₁ + x₂ + 3M – 3x₁M – x₂M =

= (4 – 3M)x₁ + (1 – M)x₂ + 3M;

Z – (- 4 +3M)x₁ – (- 1 + M)x₂ = 3M.

№2а. максимизировать: Z = x₁ + x₂

при ограничениях: 2x₁ + 3x₂ = 5

7x₁ + 2x₂  6 x₁; x₂  0.

С.ф:

Максимизировать: Z = x₁ + x₂

При ограничениях: 2x₁ + 3x₂ = 5

7x₁ + 2x₂ + x₃ = 6 x₁; x₂; x₃  0.

Максимизировать: Z = x₁ + x₂ – M(5 – 2x₁ – 3x₂) = x₁ + x₂ – 5M + 2x1M +

+ 3x₂M = (1 + 2M)x₁ + (1 + 3M)x₂ = -5M;

Z – (- 1 – 2M)x₁ + (-1 – 3M)x₂ = -5M.

б) минимизировать: Z = x₁ + x₂ + x₃ + x₄

при ограничениях: 2x₁ + x₂ + x₃ = 7

4x₁ + 8x₂ + x₄ = 8

x₃ = 7 – 2x₁ – x₂

x₄ = 8 – 4x₁ – 8x₂

Z = x₁ + x₂ +(7 – 2x₁ – x₂)+(8 - 4x₁ - 8x₂) = x₁ + x₂ + 7– 2x₁ – x₂ + 8 – 4x₁ –8x₂=

= - 5x₁ – 11x₁ + 15

Z +5x₁ + 11x₂ = 15

Упражнения:

1. Применительно к рассматриваемому примеру запишите Z – уравнения начальной С – Т для каждого из следующих вариантов изменения модели.

а). В третьем ограничении поставлен знак .

Ответ: Z + (-4 + 8 M)x₁ + (-1 + 6M)x₂ – Mx₃ – Mx₄ = 13M.

Искусственные переменные вводятся в каждое из трех уравнений.

б). Во втором ограничении поставлен знак .

Ответ: Z + (-4 + 3M)x₁ + (-1 + M)x₂ = 3M.

Искусственные переменные вводится только в 1-ое уравнение.

в). Целевая функция: Z = 4x₁ + x₂ подлежит максимум.

Ответ: Z + (-4 – 7M)x₁ + (-1 – 4M)x₂ + Mx₃ = -9M.

Искусственные переменные вводятся в 1-ое и 2-ое уравнения.

2. Необходимо ли использование искусственных переменных для получения начального решения в следующих задачах? (Все переменные неотрицательны).

а). Максимизировать: Z = x₁ + x₂

при ограничениях 2x₁ + 3x₂ = 5

7x₁ + 2x₂ 6

Ответ: Да, следует ввести искусственные переменные R₁ в первое уравнение и остаточные переменные – во второе.

б). Минимизировать: Z = x₁ + x₂ + x₃ + x₄

при ограничениях 2x₁ + x₂ + x₃ = 7

4x₁ + 8x₂ + x₄ = 8

Ответ: Нет, следует использовать переменные х₃ и х₄, предварительно исключив их из целевой функции путем подстановок

х₃ = 7 – 2х₁ – х₂

х₄ = 8 – 4х₁ – 3х₂.

Двухэтапный метод

Недостаток М-метода связан с возможностью ошибок в вычисле­ниях, обусловленных очень большой величиной коэффициента М. Чтобы пояснить это, допустим, что в примере из подразд. 3.2.3 значение М было принято равным 100 000. Тогда коэффициенты при х₁ и х₂ в z-уравнении начальной симплекс-таблицы будут равны (—4+700000) и (—1+400000) соответственно. Из-за большой величины М вклад исходных коэффициентов (4 и 1) оказывается ничтожным. Вследствие ошибок округления, свойственных любой цифровой ЭВМ, процесс вычислений может стать нечувстви­тельным к значениям исходных коэффициентов при х_х и х₂. При этом возникает опасность того, что эти переменные будут интерпретиро­ваться как переменные, фигурирующие в целевой функции с нуле­выми коэффициентами.

Двухэтапный метод позволяет избежать этих затруднений. При использовании двухэтапного метода искусственные переменные вводятся таким же образом, как и в М-методе. Однако коэффициент М при этом не фигурирует, что достигается расчленением процесса решения задачи на два этапа (отсюда и название метода - двух­этапный). Этапы реализации данного метода включают следующие процедуры.

Этап I. Вводятся искусственные переменные, необходимые для получения стартовой точки. Записывается новая целевая функ­ция, предусматривающая минимизацию суммы искусственных пере­менных при исходных ограничениях, видоизмененных за счет вве­дения искусственных переменных. Если минимальное значение но­вой целевой функции равно нулю (т. е. все искусственные перемен­ные имеют в оптимуме нулевые значения), исходная задача имеет допустимое решение. Переходят к этапу II. В противном случае, когда минимум новой целевой функции оказывается больше нуля, исходная задача не имеет допустимых решений, и процесс вычисле­ний заканчивается.

Э т а п II. Оптимальное базисное решение, полученное на этапе I, используется в качестве начального решения исходной задачи.

Реализацию двухэтапного метода проиллюстрируем опять на примере из подразд. 3.2.3.

Этап I. Так как необходимо ввести искусственные переменные R₁ и R₂ в первое и второе уравнения соответственно, этап I сводится к

Минимизации r = R₁ + R₂

при ограничениях

3x₁ + x₂ + R₁ =3,

4x₁ + 3x₂ – x₃ + R₂ = 6,

x₁ + 2x₂ + x₄ = 4,

x₁, x₂, x₃, R₁, R₂, x₄  0.

Поскольку R₁ и R₂ фигурируют в начальном решении, следует подставить в целевую функцию их выражения, полученные из соот­ветствующих ограничений (сравните с процедурой, использованной в М -методе):

r = R₁ + R₂ = (3 – 3x₁ – x₂) + (6 – 4x₁ – 3x₂ + x₃) = - 7x₁ – 4x₂ + x₃ + 9.

С помощью этого соотношения получим начальную симплекс-таблицу:

Базисные переменные	x1 x2 x3 R1 R2 x4	Решение
r	7 4 -1 0 0 0	9
R1	3 1 0 1 0 0 4 3 -1 0 1 0 1 2 0 0 0 1	3
R2		6
x4		4

Оптимальная таблица, получаемая за две итерации, имеет следующий вид. (Проверьте!)

Базисные переменные	x1 x2 x3 R1 R2 x4	Решение
r	0 0 0 -1 -1 0	0
R1	1 0 1/5 3/5 -1/5 0 0 1 -3/5 -4/5 3/5 0 0 0 1 1 -1 1	3/5 6/5 1
R2
x4

Так как r = 0, задача имеет допустимое решение, и можно перходить к этапу II.

Этап II. Искусственные переменные уже выполнили свою функцию, так что во всех последующих вычислительных процедура они фигурировать не должны. Поэтому запишем уравнения из оптимальной симплекс-таблицы этапа I в следующем виде:

х₁ + 1/5х₃ = 3/5,

х₂ – 3/5х₃ = 6/5,

х₃ + х₄ = 1.

Эти уравнения полностью эквивалентны уравнениям исходной зада­чи, записанной в стандартной форме (до введения искусственных переменных). Поэтому исходную задачу можно сформулировать сле­дующим образом;

минимизировать z = 4x1 + x₂

при ограничениях

х₁ + 1/5х₃ = 3/5,

х₂ – 3/5х₃ = 6/5,

х₃ + х₄ = 1,

х₁, х₂, х₃, х₄  0.

Главная цель первого этапа вычислений состоит в том, чтобы обеспечить получение начального решения исходной задачи. Так как задача содержит три уравнения и четыре переменные, то, при­писывая одной (4—3==1) из переменных, а именно х₃, нулевое зна­чение, можно сразу получить начальное допустимое базисное реше­ние: х₁ = 3/5, х₂ = 6/5 и х₄ = 1.

Для решения задачи необходимо, как и при использовании Л1-метода, подставить в целевую функцию выражения для базисных переменных а;! и л-з, получаемые из соответствующих ограничений;

z = 4х₁ + х₂ = 4 (3/5 – 1/5х₃) + (6/5 + 3/5х₃) = -1/5х₃ + 18/5.

В результате будем иметь следующую начальную симплекс-таблицу для этапа II:

Базисные переменные	x1 x2 x3 x4	Решение
r	0 0 1/5 0	18/5
R1	1 0 1/5 0 0 1 -3/5 0 0 0 1 1	3/5 6/5 1
R2
x4

Решение, представленное в данной таблице, не оптимально, так как переменная х₃ подлежит включению в базис. Если выполнить необходимые вычислительные процедуры симплекс-алгоритма, оп­тимальное решение будет получено за одну итерацию. (Проверьте!)

Следует отметить, что количество необходимых итераций М-метода и двухэтапного метода всегда одинаково, и между симплекс-таблицами, получаемыми при использовании этих методов, имеет место взаимно-однозначное соответствие. Преимущество двухэтапного метода состоит в том, что при его реализации не требуется использование в расчетах постоянной М.

Следует подчеркнуть, что на этапе II искусственные переменные не фигурируют только в том случае, если в конце этапа I они становятся небазисными переменными (как это было в рассмотренного примере). Однако возможен и такой случай, когда при завершении этапа I искусственные переменные, имея нулевые значения, остаются базисными. Это требует принятия особых мер предосторожности, исключающих возможность появления положительных искусственных переменных на этапе II вычислений. С деталями соответствующих процедур можно познакомиться в книге [2, разд. 5.2].

Упражнение 3.2.5

(а) Как можно интерпретировать искусственные переменные, используемые на этапе I двухэтапного метода? В частности, почему необходимо минимизировать сумму искусственных переменных?

[Ответ. Искусственные переменные можно рассматривать как «меру недопустимости» при проверке выполнения исходных ограничений. Когда минимум суммы (неотрицательных) искусственных переменных равен нулю каждая из этих искусственных переменных имеет нулевое значение. По этому получаемое базисное решение является допустимым решением исходной задачи.]

(б) Следует ли максимизировать сумму искусственных переменных на этапе I, если целевая функция исходной задачи ЛП подлежит максимизации?

[Ответ. Нет, в рамках этапа I всегда осуществляется минимизация, так как именно процесс минимизации эквивалентен «штрафованию» искусственных переменных.]

Лекция 9:

ИНТЕРПРЕТАЦИЯ СИМПЛЕКС - ТАБЛИЦ. АНАЛИЗ МОДЕЛИ НА ЧУВСТВИТЕЛЬНОСТЬ

Выше были рассмотрены вычислительные процедуры СМ. ЭВМ полностью освобождает от необходимости осуществлять трудоемкий процесс решения задач ЛП вручную. Для этого имеется широкий набор разнообразных машинных программ, позволяющих выполнять соответствующие вычисления на ЭВМ как в пакетном режиме, так и в режиме обращения к ЭВМ с терминальных устройств. Приняв непосредственное участие в исследованиях, связанных с разработкой линейных оптимизационных моделей и решением практических задач ЛП, можно убедиться в том, что большую часть времени в работе занимает построение модели, сбор необходимых данных и подготовка входной информации для машинных программ. Всю остальную часть работы выполняет ЭВМ, проводя вычисления и выдавая их результаты в виде оптимального решения задачи.

Из вышеизложенного следует, что основное внимание следует теперь уделить интерпретации и анализу результатов, полученных с помощью ЭВМ. Однако, было бы ошибочным считать, что интерпретация информации, выведенной ЭВМ на печать, возможна без ясного представления о том, почему и как «работает» СМ. Соответствующие вопросы мы рассмотрели выше. Следует еще раз подчеркнуть важность понимания положений, определяющих возможность применения СМ. В противном случае всегда есть опасность получения ошибочных решений и как следствие «вотума недоверия».

Исследователя вряд ли устроила бы заключительная С – Т, из которой можно было бы получить только список переменных и их значения. На самом же деле результирующая С – Т « насыщена» весьма важными данными, лишь небольшую часть которых составляют оптимальные значения переменных. Из С-Т либо непосредственно, либо при помощи простых дополнительных вычислений можно получить информацию относительно

1. оптимального решения,

2. статуса ресурсов,

3. ценности каждого ресурса,

4. чувствительности оптимального решения к изменению запасов ресурсов, вариациям коэффициентов целевой функции и интенсивности потребления ресурсов.

Сведения, относящиеся к первым трем пунктам, можно извлечь непосредственно из С – Т для оптимального решения. Получение информации, относящейся к 4-му пункту, требует дополнительных вычислений.

Для иллюстрации возможностей получения указанной выше интерпретации из заключенной С – Т воспользуемся опять задачей фирмы Reddy Mikks Эта задача формируется следующим образом:

Максимизировать: Z = 3x_E + 2x₁ (прибыль)

При ограничениях: x_E + 2x₁ +S₁ = 6 (продукт А)

2х_E + x₁ + S₂ = 8 (продукт В)

-x_E + x₁ + S₃ = 1 (спрос)

x₁ + S₄ = 2 (спрос)

x_E, S₁; S₂; S₃; S₄  0

Оптимальная С – Т имеет вид:

Базисные переменные	xe	xi	S1	S2	S3	S4	Решение
z	0	0	1/3	4/3	0	0	12 х 2/3
х1	0	1	2/3	-1/3	0	0	1х 1/3
хе	1	0	-1/3	2/3	0	0	3х 1/3
S3	0	0	-1	1	1	0	3
S4	0	0	-2/3	1/3	0	1	2/3

Оптимальное решение.

С точки зрения практики использования результатов решения задач ЛП классификация переменных, предусматривающая их разделение на базисные, не имеет значения и при анализе данных, характеризующее оптимальное решение, может не учитываться.

Переменные, отсутствующие в столбце «Базисные переменные», обязательно имеют нулевое значение. Значения остальных переменных приводятся в столбце «Решение». При интерпретации результатов оптимизации в задаче фирмы Reddy Mikks нас прежде всего интересуют объемы производства красок для внутренних (I) и наружных (E) работ, то есть значения управляемых переменных Х₁ и Х_Е. Используя данные, содержащиеся с С – Т для оптимального решения, основные результаты можно представить в следующем виде:

Управляемые переменные	Оптимальные решения	Решение
хЕ	3 1/3	Объем производства краски Е должен быть равен 3 1/3т. в сутки
Х1	1 1/3	Объем производства краски I должен быть равен 1 1/3т. в сутки
Z	12 2/3	Прибыль от реализации продукции равна 12 2/3тыс.долл. (в сутки)

Заметим, что Z = 3х_Е + 2х_I = 3(3 1/3) + 2(1 1/3) = 12 2/3. Это соответствует данным заключительной С – Т.

Статус ресурсов.

Ресурсы относят к дефицитным или недефицитным в зависимости от того, полное или частичное их использование предусматривает оптимальное решение задачи. Сейчас цель состоит в том, чтобы получить соответствующую информацию непосредственно из С – Т для оптимального решения. Однако сначало следует четко уяснить следующее. Говоря о ресурсах, фигурирующих в задачи ЛП, мы подразумеваем, что установлены некоторые максимальные пределы их запасов, поэтому в соответствующих исходных ограничениях должен использоваться знак . Следовательно, ограничения со знаком  не могут рассматриваться как ограничения на ресурсы. Скорее, ограничения такого типа отражают то обстоятельство, что решение должно удовлетворять определенным требованиям, например, обеспечению минимального спроса или минимальных отклонений от установленных структурных характеристик производства (сбыта).

В модели, построенной для фирмы Reddy Mikks, фигурируют 4 ограничения со знаком . Первые два ограничения (определяющие допустимый расход исходных продуктов) представляют собой «истинные» ограничения на ресурсы. 3-е и 4-е ограничения относятся к спросу. Эти требования можно рассматривать как ограничения на соответствующие «ресурсы», так как увеличение спроса на продукцию эквивалентно расширению «представительства» фирмы на рынке сбыта. В отношении финансовых средств такая ситуация имеет те же последствия, что и увеличение запасов ресурсов (исходных продуктов), требующее распределение дополнительных вложений.

Таким образом, следует, что статус ресурсов (дефицитный или недефицитный) для любой модели ЛП можно установить непосредственно из результирующей С – Т, обращая внимание на значения остаточных переменных. Применительно к задаче фирмы Reddy Mikks можно привести следующую сводку результатов:

Ресурс	Остаточная переменная	Статус Ресурса
Исходный продукт А	S1 = 0	Дефицитный
Исходный продукт В	S2 = 0	Дефицитный
Повышение объема производства краски I по отношению к объему производства краски Е	S3 = 3	Недефицитный
Спрос на краску I	S4 = 2/3	Недефицитный

Положительное значение остаточной переменной указывает на неполное использование соответствующего ресурса, то есть данный ресурс является недефицитным. Если же остаточная переменная = 0, это свидетельствует о полном потреблении соответствующего ресурса. Из таблицы видно, что ресурсы 3 и 4, связанные с возможностями сбыта продукции, является недефицитным. Поэтому любое увеличение их запасов сверх установленного максимального значения приведет лишь к тому, что они станут еще более недефицитными. Оптимальное решение задачи при этом остается неизменным.

Ресурсы, увеличение запасов которых позволяет улучшить решение (увеличить прибыль), - это исходные продукты А и В, поскольку из С – Т для оптимального решения видно, что они дефицитны. В связи с этим логично поставить следующий вопрос: какому из дефицитных ресурсов следует отдать предпочтение при вложении дополнительных средств на увеличение их запасов, с тем чтобы получить от них максимум отдачу? Ответ на этот вопрос будет дан в следующей теме, где рассмотрим ценность ресурсов.

Пример: Применительно к задаче фирмы Reddy Mikks найти экономическую интерпретацию оптимальным значением остаточных переменных S₃ = 3 и S₄ = 2/3

Ответ: Так как Х_Е - Х₁ = S₃ – 1, то переменная S₃ характеризует увеличенное на 1т. превышение объема производства краски Е по отношению к объему производства краски I. Таким образом, S₃ = 3 соответствующее случаю, когда объем производства краски Е превышает объем производства краски I на 2т. Переменная S₄ характеризует предельное увеличение производства краски I, при котором не будет превышен максимум спрос на рынке сбыта.

Ценность ресурса.

Ценность ресурса характеризуется величиной улучшения оптимального значения Z, приходящегося на единицу прироста объема данного ресурса. Графическая интерпретация этого определения применительно к условиям задачи фирмы Reddy Mikks была дана выше. Прежде чем продолжить изучение данного вопроса, целесообразно вернуться к рис. Графический анализ показывает, что ценность ресурсов 1, 2, 3 и 4 равна.

Y₁ = 1/3 тыс. долл. на 1т. прироста запасов ресурса А,

Y₂ = 4/3 тыс. долл. На 1т. прироста запасов ресурса В,

Y₃ = 0, Y₄ = 0.

Эта информация представлена в С – Т для оптимального решения задачи. Обратим внимание на значения коэффициентов Z – уравнения, состоящих при переменных начального базиса S₁, S₂, S₃ и S₄.

р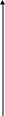 ис. С: (3 1/3, 1 1/3); Z = 12 1/3; К(3,2); Z = 13

X₁

Е D K

3 4 1 C Ресурс А = 7т.

F 5 6 2 Ресурс А = 6т.

A B Х_Е

Выделим для удобства соответствующую часть С – Т:

Базисные переменные	ХЕ Х1 S1 S2 S3 S4	Решение
Z	0 0 1/3 4/3 0 0	12 2/3

Значения указанных коэффициентов (1/3; 4/3; 0; 0 ) в точности соответствуют значениям у₁; у₂; у₃; у₄. Как следует из теории решения задач ЛП, ценность ресурсов всегда можно определить по значениям коэффициентов при переменных начального базиса, фигурирующих в Z – уравнении оптимальной С – Т. Так как переменная S_i всегда связана только с ресурсом i, идентификация ресурса по коэффициенту не должна вызывать затруднений.

Покажем, каким образом аналогичный результат можно получить непосредственно из С – Т для оптимального решения задачи фирмы Reddy Mikks.

Z = 12 2/3 – (1/3S₁ + 4/3S₂ + 0S₃ + 0S₄)

Положительное приращение переменной S₁ относительно ее текущего нулевого значения приводит к пропорциональному уменьшению Z, причем коэффициент пропорциональности = 1/3тыс. долл./т. Но, как следует из первого ограничения модели,

Х_Е + 2Х₁ + S₁ = 6,

Увеличение S₁ эквивалентно снижению запаса ресурса 1 (продукта А). Отсюда следует, что уменьшение запаса первого ресурса вызывает пропорциональное уменьшение целевой функции с тем же коэффициентом пропорциональности, равным 1/3тыс. долл./т. Так как мы оперируем с линейными функциями, полученный вывод можно обобщить, считая, что и увеличение запаса первого ресурса (эквивалентно введению избыточной переменной S₁ < 0) приводит к пропорциональному увеличению Z с тем же коэффициентом пропорциональности, равным 1/3тыс. долл./т. Аналогичные рассуждения справедливы для ресурса 2.

В отношении ресурсов 3 и 4 было установлено, что их ценность = 0 (у₃ = у₄ = 0). Этого и следовало ожидать, так как ресурсы 3 и 4 оказались недефицитными. Такой результат получается всякий раз, когда соответствующие остаточные переменные имеют положительное значение.

Несмотря на то, что ценность различных ресурсов, определяемая значениями переменных у_i, была представлена в стоимостном (тыс. долл.) выражении, ее нельзя отождествлять с действительными ценами, по которым возможна закупка соответствующих ресурсов. На самом деле речь идет о некоторой мере, имеющей экономическую природу и количественно характеризующей ценность ресурса только относительно полученного оптимального значения целевой функции. При изменении ограничений модели соответствующие экономические оценки будут меняться даже тогда, когда оптимизируемый процесс предполагает применение тех же ресурсов. Поэтому при характеристики ценность ресурсов экономисты предпочитают использовать такие термины, как теневая цена, скрытая цена или более специфический термин – двойственная оценка.

Упражнение: Предположим, что в задаче фирмы Reddy Mikks целевая функция Z = 3х_Е + 2х₁ заменена на Z = 2х_Е + 5х₁; а ограничения модели не изменились. Решение задачи с помощью СМ приводит к следующему Z – уравнению:

Z + 2S₁ + S₄ = 14.

Оптимальные значения переменных равны Х_Е = Х₁ = 2 , S₂ = 2 S₃ = 1. Все остальные переменные имеют нулевое значение.

1. Определите статус каждого из 4 ресурсов, фигурирующих в модели.

Ответ: Ресурсы 1 и 4 дефицитные, ресурсы 2 и 3 недефицитные.

2. Определите теневую цену каждого из 4-х ресурсов.

Ответ: у₁ = 2; у₂ = у₃ = 0; у₄ = 1.

3. Можно ли улучшить оптимальное значение Z, увеличив запас продукта В?

Ответ: Нет, поскольку у₂ = 2, то есть данный ресурс является недефицитный.

4. Так как у₄ = 1, то, увеличение 4-го ресурса, можно добиться улучшения оптимального значения Z. Дайте экономическую интерпретацию увеличению объема «использования» четвертого ресурса.

Ответ: Четвертое ограничение фиксирует предельный уровень спроса. Увеличение объема «использования» 4-го ресурса эквивалентна увеличению сферы влияния фирмы на рынке сбыта.

5. Какому из ресурсов следует отдать предпочтение при вложении дополнительных средств?

Ответ: Вложения следует направить прежде всего на увеличение запасов продукта А, так как ему соответствует наибольшая теневая цена у₁ = 2.

Максимальное изменение запаса ресурса

При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используются теневые цены. Чтобы определить интервал значений изменения запаса ресурса, при которых теневая цена данного ресурса, фигурирующая в заключительной симплекс-таблице, остается неизменной, необходимо выполнить ряд дополнительных вычислений. Рассмотрим сначала соответствующие вычислительные процедуры, а затем покажем, как требуемая информация может быть получена из симплекс-таблицы для оптимального решения.

Положим, что в задаче фирмы Reddy Mikks запас первого ре­сурса изменился на ₁ т. е. запас продукта А составит 6+₁ тонн. При положительной величине ₁ запас данного ресурса увеличи­вается, при отрицательной - уменьшается. Как правило, иссле­дуется ситуация, когда объем ресурса увеличивается (₁0). Однако, чтобы получить результат в общем виде, рассмотрим оба случая.

Как изменится симплекс-таблица при изменении величины за­паса ресурса на ₁? Проще всего получить ответ на этот вопрос, если ввести ₁ в правую часть первого ограничения начальной сим­плекс-таблицы и затем выполнить все алгебраические преобразова­ния, соответствующие последовательности итераций. Поскольку правые части ограничений никогда не используются в качестве ведущих элементов, то очевидно, что на каждой итерации ₁ будет оказывать влияние только на правые части ограничений. Читателю предлагается самостоятельно проверить, что результаты, получае­мые на соответствующих итерациях при решении рассматриваемой задачи, идентичны данным, приведенным в табл. 3.7.

Таблица 3.7

Уравнение	Значения элементов правой части на соответствующих итерациях
	(начало вычислений)	1	2 (оптимум)
Z	0	12
1	6 + 1	2 + 1
2	8	4
3	1	5	3-11
4	2	2

Фактически все изменения правых частей ограничений, обуслов­ленные введением ₁ , можно определить непосредственно по данным, содержащимся в симплекс-таблицах. Прежде всего заметим, что на каждой итерации новая правая часть каждого ограничения пред­ставляет собой сумму двух величин: 1) постоянной и 2) члена, ли­нейно зависящего от ₁ . Постоянные соответствуют числам, которые фигурируют на соответствующих итерациях в правых частях ограничений симплекс-таблиц до введения ₁. Коэффициенты при ₁ во вторых слагаемых равны коэффициентам при s₁ на той же ите­рации. Так, например, на последней итерации (оптимальное реше­ние) постоянные (12* 2/3, 4/3, 10/3, 3, 2/3) представляют собой числа, фигурирующие в правых частях ограничений оптимальной симп­лекс-таблицы до введения ₁. Коэффициенты (1/3, 2/3, -1/3, -1, 2/3) равны коэффициентам при s₁ в той же симплекс-таблице пото­му, что эта переменная связана только с первым ограничением. Другими словами, при анализе влияния изменений в правых частях второго, третьего и четвертого ограничений нужно пользоваться коэффициентами при переменных s₂, s₃ и s₄ соответственно.

Какие выводы можно сделать из полученных результатов? Так как введение ₁ сказывается лишь на правой части симплекс-таблицы, изменение запаса ресурса может повлиять только на допустимость решения. Поэтому ₁ не может принимать значений, при которых какая-либо из (базисных) переменных становится отри­цательной. Из этого следует, что величина ₁ должна быть огра­ничена таким интервалом значений, при которых выполняется ус­ловие неотрицательности правых частей ограничений в результи­рующей симплекс-таблице, т. е.

X₁ = 4/3 + (2/3)₁  0, (1)

X_E = 4/3 + (1/3) ₁  0, (2)

S₃ = 3 - ₁  0, (3)

S₄ = 2/3 – (2/3) ₁  0. (4)

Для определения допустимого интервала изменения ₁ рассмо­трим два случая.

Случай 1: ₁ > 0. Соотношение (1) всегда выполняется при ₁  0. Соотношения (2), (3) и (4) определяют следующие предельные зна­чения ₁ : ₁  10, ₁  3 и ₁  1. Таким образом, все четыре соот­ношения выполняются при ₁  1.

Случай 2: ₁ < о. Соотношения (2), (3) и (4) всегда выполняются при ₁ <о, тогда как соотношение (1) справедливо только при ₁  -2.

Объединяя результаты, полученные для обоих случаев, можно сделать вывод, что при –2  ₁  1 решение рассматриваемой зада­чи всегда будет допустимым. Любое значение ₁, выходящее за пределы указанного интервала (т. е. уменьшение запаса продукта А более чем на 2 т или увеличение более чем на 1 т), приведет к недопу­стимости решения и новой совокупности базисных переменных (см. гл. 4).

Упражнение 3.4.3. Рассмотрите задачу фирмы Reddy Mikks.

(а) Найдите новое оптимальное решение задачи, если ₁ ==1/2 т. [Ответ: z = 125/6, x_E = 3 1/6, x₁ = 2/3, s₁ = s₂ = 0, s₃ = 2 ½, s₄ = 1/3.]

(б) Определите правые части ограничений заключительной симплекс-таблицы

- при изменении запасов ресурсов 2, 3 и 4 на ₂, ₃ и ₄ соответственно.

[Ответ: ₂ : 4/3 - ₂/3, 10/3 +2₂/3, 3 + ₂, 2/3 + ₂/3;

₃ : 4/3, 10/3, 3+₃, 2/3;

₄ : 4/3, 10/3, 3, 2/3 + ₄.]

(в) Применительно к п. (б) определите допустимые интервалы изменения ₂, ₃ и ₄.

[Ответ: ₂ : -2  ₂  4, -3  ₃  , -2/3  ₄  ,]

(г) Определите интервалы изменения оптимальных значений z, соответствующие результатам, полученным в п. (в).

[Ответ: ₂ : 10  z  18. ₃ и ₄ : z = 122/3 независимо от значений з и ₄. Эти результаты согласуются с результатами выполненного ранее анализа ценности ресурсов.]

(д) Будут ли справедливы результаты, полученные в п. (г), если ₂, ₃ и ₄ вво­дятся одновременно?

[Ответ. Нет, поскольку при одновременном изменении запасов ресурсов 2, 3 и 4 элементы правых частей ограничений симплекс-таблицы становятся функциями ₂, з и ₄. Полученные ранее результаты справедливы лишь тогда, когда рассматривается изменение запаса только одного из ресурсов.]

Максимальное изменение коэффициентов удельной

прибыли (стоимости)

Наряду с определением допустимых изменений запасов ресур­сов представляет интерес и установление интервала допустимых изменений коэффициентов удельной прибыли (или стоимости). В подразд. 2.1.2 (третья задача анализа на чувствительность) на основе графического представления модели было показано, что при определенных значениях изменения коэффициентов целевой функции оптимальные значения переменных остаются неизменными (хотя оптимальное значение z при этом меняется). Возвращаясь к этому вопросу, покажем, каким образом интересующую нас ин­формацию можно получить из данных, содержащихся в заключи­тельной симплекс-таблице.

Следует отметить, что уравнение целевой функции также ни­когда не используется в качестве ведущего уравнения. Поэтому лю­бые изменения коэффициентов целевой функции окажут влияние только на z-уравнение результирующей симплекс-таблицы. Это означает, что такие изменения могут сделать полученное решение неоптимальным. Наша цель заключается в том, чтобы найти интер­валы значений изменений коэффициентов целевой функции (рас­сматривая каждый из коэффициентов отдельно), при которых оп­тимальные значения переменных остаются неизменными.

Чтобы показать, как выполняются соответствующие вычисле­ния, положим, что удельная прибыль от производственной деятель­ности, ассоциированной с переменной x_E (задача фирмы Reddy Mikks) изменяется от 3 до 3+ ₁ , где ₁ может быть как положитель­ным, так и отрицательным числом. Целевая функция в этом случае принимает следующий вид:

Z = (3 + ₁) x_E + 2x₁.

Если воспользоваться данными начальной симплекс-таблицы и выполнить все вычисления, необходимые для получения заключи­тельной симплекс-таблицы, то последнее z-уравнение будет выгля­деть следующим образом:

Базисные переменные	xE x1 s1 s2 s3 s4	Решение
z	0 0 0 0

Коэффициенты при базисных переменных x_E, x₁ и остаточных переменных s₃, s₄ остаются равными нулю. Это уравнение отличается от z-уравнения до введения ₁ только наличием членов, содержащих ₁. Коэффициенты при ₁ равны коэффициентам при соответствующих переменных в x_E-уравнении симплекс-таблицы для полученного ра­нее оптимального решения

Базисные переменные	xE x1 s1 s2 s3 s4	Решение
xE	1 0 -1/3 2/3 0 0	10/3

Мы рассматриваем x_E-уравнение, так как коэффициент именно при этой переменной в выражении для целевой функции изменился на ₁.

Оптимальные значения переменных будут оставаться неизмен­ными при значениях ₁, удовлетворяющих условию неотрицатель­ности (задача на отыскание максимума) всех коэффициентов при не­базисных переменных в z-уравнении. Таким образом, должны вы­полняться следующие неравенства:

1/3 - ₁/3  0, (1)

4/3 +2₁/3  0. (2)

Из первого неравенства получаем, что ₁  1, а из второго следует, что 1  -2. Эти результаты определяют пределы изменения ко­эффициента c₁ в виде следующего соотношения: -2  ₁  1. Та­ким образом, при уменьшении коэффициента целевой функции при переменной хе до значения, равного 3+ (—2)==1, или при его уве­личении до 3+1 ==4 оптимальные значения переменных остаются неизменными (сравните с результатом, полученным при рассмотре­нии третьей задачи анализа на чувствительность, подразд. 2.1.2). Однако оптимальное значение z будет изменяться (в соответствии с выражением где –2  ₁  1).

Упражнение 3.4.4. Пусть в задаче фирмы Reddy Mikks коэффициент це­левой функции при переменной x₁ изменился на величину ₂. Определите интер­вал значений бд, при которых оптимальные значения переменных остаются неизменными.

[Ответ: -1/2  ₂  4, z = 12 2/3 + 4/3 ₂.]

Все предыдущее обсуждение касалось исследования изменений коэффициента при переменной, которой поставлено в соответствие ограничение, фигурирующее в симплекс-таблице. Однако такое ограничение имеется лишь в том случае, когда данная переменная является базисной (например, x_E и x₁). Если переменная небазис­ная, то в столбце, содержащем базисные переменные, она не будет представлена.

Любое изменение коэффициента целевой функции при небазисной переменной приводит лишь к тому, что в заключительной симплекс-таблице изменяется только этот коэффициент. Рассмотрим в ка­честве иллюстрации случай, когда коэффициент при переменной s₁ (первой остаточной переменной) изменяется от 0 до ₃. Выполне­ние преобразований, необходимых для получения заключительной симплекс-таблицы, приводит к следующему результирующему z-уравнению:

Базисные переменные	xE x1 s1 s2 s3 s4	Решение
z	1 0 1/3-3 4/3 0 0	12 2/3

Из приведенного фрагмента заключительной симплекс-таблицы вид­но, что единственное отличие от z-уравнения до введения 6з состо­ит в том, что коэффициент при s₁ уменьшился на ₃. Таким образом, коэффициент при небазисной переменной в результирующем z-уравнении нужно уменьшить на ту же величину, на которую он увеличивается в исходном z-уравнении.

Задачи: Тема: СМ и вычислительные процедуры С –Т.

№3.3. Задано трехмерное пространство решений задачи ЛП с экстремальными точками А, В, С,…J. Координаты этих точек указаны на рис.

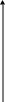Х₃

A: (0;0;0)

D G В: (1;0;0)

С: (0;1;0)

F J H D: (0;0;1)

B X₁

A I

C E

X₂ рис. 1.

а) Являются ли следующие пары экстремальных точек смежными? (А;В) (В;D) (E;H) (A;I)

б) Пусть процесс решения задачи с помощью СМ начинается с т. А и заканчивается нахождением оптимума в т. H путём реализации следующих переходов от одной экстремальной точки к другой?

1). А  B  G  H 4). A  I  H

2). A  F  J  H 5). A  D  G  H

3). A  C  I  H 6). A  D  A  B  G  H

7). A  C  F  D  A  B  G  H

№3.4. На рис.1 все ограничения, определяющие пространство решений, имеют знак . Пусть S₁; S₂; S₃ и S₄ – остаточные переменные, ассоциированные с ограничениями, которые представляются плоскостями CEIJF, BEIHG, DFJHG и HIJ соответственно. Идентифицируйте базисные и небазисные переменные, соответствующие каждой допустимой экстремальной точке. (Указание: подразумевается, что Х₁; Х₂; Х₃  0)

№3.5. Для условий задачи 3.4. определите включаемые в базис и исключаемые из базиса переменные для итераций, соответствующие переходам между следующими парами экстремальных точек:

A  B; E  I; F  J; D  G.

№3.6. Рассмотрим следующую задачу:

максимизировать: Z = 2х₁ – 4х₂ + 5х₃ + 8х₄

при ограничениях: х₁ + 4х₂ – 2х₃ + 8х₄  2

-х₁ + 2х₂ +3х₃ + 4х₄  1

х₁; х₂; х₃; х₄  0.

а). Определите мах количество возможных базисных решений?

б). Идентифицируйте допустимые экстремальные точки.

в). Найдите д. Б. Р.

№3.7. Пусть при решение задачи, условия которой соответствуют рис.1., исходной точкой ( начальным решением) является точка А. Определите переменную, вводимую в базис на первой итерации, значение этой новой базисной переменной и улучшение значения максимальной целевой функции, если она имеет следующий вид:

а). Z = х₁ – 2х₂ + 3х₃

б). Z = 5х₁ + 2х₂ +4х₃

в). Z = -2х₁ + 7х₂ + 2х₃

г). Z = х₁ + х₂ +х₃

№ 3.8. Пусть для условий, соответствует рис. 2 задана следующая целевая функция:

максимизировать: Z = 3х₁ + 6х₂

Х₂ рис.2 Х₂

4 4

3 3

2 F 2 F E D

1 G G 1 C

0 A Х₁ А B Х₁

- 1 -1 1 2 3 4 5 -1 -1 1 2 3 4 5

а). Найдите графическим способом оптимальную экстремальную точку.

б). Пологая, что реализация СМ начинается с т. А, определите последовательность экстремальных точек, приводящую к оптимуму, найденному в п.(а).

в). Пологая, что реализация СМ начинается с т. А, определите вводимую в базис переменную и отношения, используемые при проверке условия допустимости, если целевая функция имеет вид:

максимизировать: Z = 4х₁ + х₂

д). Применительно к условиям пп. (в) и (г) определите результирующее улучшение целевой функции.

№ 3.9. Дана следующая система уравнений:

х₁ + 2х₂ – 3х₃ + 5х₄ + х₅ = 4

5х₁ – 2х₂ + 6х₄ + х₆ = 8

2х₁ + 3х₂ – 2х₃ + 3х₄ + х₇ = 3

-х₁ + х₃ + 2х₄ + х₈ = 0

х₁; х₂ … х₈  0.

Известно начальное базисное решение (х₅ … х₈) базис вводится переменная х₁. Какая из переменных предыдущего базиса должна стать нулевой небазисной переменной, чтобы все переменные остались неотрицательными, и каково значение х₁ в новом базисном решении? Дайте ответ на поставленные вопросы для случаев, когда в базис вводятся переменные х₂; х₃; х₄.

№3.10. В нижесл. таблице приведены результаты некоторой итерации СМ.

Базисные переменные	х1 х2 х3 х4 х5 х6 х7 х8	Решение
Z	0 -5 0 4 -1 -10 0 0	620
Х8 Х3 Х1	0 3 0 -2 -3 -1 5 1 0 2 1 3 1 0 3 0 1 -1 0 0 6 -4 0 0	12 6 0

а). Определите исключаемую из базиса переменную, если в базис вводятся переменные: 1) х₂; 2) х₄; 3) х₅; 4) х₆; 5) х₇.

б). Для каждого из случаев, перечисленных в пункте (а), определите результирующее увеличение или уменьшение целевой функции Z.

№ 3.11. Решите следующие системы линейных уравнений, используя процедуру преобразования спрос (Гаусса – Жордана), являющуюся составной частью СМ.

а). –3х₁ + 2х₂ + 5х₃ = 5

4х₁ + 3х₂ + 2х₃ = 8

х₁ – х₂ + 3х₃ = 10

б). х₂ + х₃ = 5 (на экзамен)

2х₁ + х₂ – х₃ = 12

х₁ + 3х₂ + 4х₃ = 10

№ 3.12. Дана следующая совокупность ограничений:

х₁ + 7х₂ + 3х₃ + 7х₄  46

3х₁ – х₂ + х₃ + 2х₄  8

2х₁ + 3х₂ – х₃ + х₄  10

Решите задачу ЛП СМ при следующих целевых функциях:

а). максимизировать Z = 2х₁ + х₂ – 3х₃ + 5х₄

б). максимизировать Z = -2х₁ + 6х₂ + 3х₃ – 2х₄

в). максимизировать Z = 3х₁ – х₂ + 3х₃ +4х₄

г). минимизировать Z = 5х₁ – 4х₂ + 6х₃ + 8х₄  (на экзамен).

д). минимизировать Z = 3х₁ – 6х₂ – 2х₃ + 4х₄

№ 3.13. Решите следующую задачу, анализируя и обосновывая ход решения, исходя из положений, на которых базируется СМ.

максимизировать Z = 5х₁ – 6х₂ + 3х₃ – 5х₄ + 12х₅

при ограничениях х₁ + 3х₂ + 5х₃ + 6х₄ + 3х₅  90

х₁ … х₅  0

№ 3.14. Рассмотрим следующую задачу ЛП:

максимизировать Z = х₁ - 3х₂ – 2х₃

при ограничениях 3х₁ – х₂ + 2х₃  7

-2х₁ + 4х₂  12

-4х₁ + 3х₂ + 8х₃  10

х_{1 ;} х₂; х₃  0.

а). Решите задачу СМ, выбирая на каждой итерации в качестве новой базисной переменной ту небазисную переменную, которая в Z – уравнение имеет наибольший положительный коэффициент.

б). Решите задачу СМ, выбирая в качестве новой базисной переменной ту небазисную переменную, которая имеет в Z – уравнение наименьший положительный коэффициент.

в). Сравните количество итераций, потребовавшихся для решения задачи в пп (а) и (б).

г). Если требование минимизации целевой функции заменяется требованием ее максимизации, исходную целевую функцию умножают на (-1), и при реализации СМ используют условие оптимальности, соответствующую процессу максимизации. Как изменяются при этом вычислительные процедуры СМ по сравнению со случаем, когда целевая функция должна была минимальна?

№3.15. Решите следующую задачу, используя для получения начального (допустимого) базисного решения переменные х₄; х₅; х₆.

минимизировать Z = 3х₁ + х₂ + 2х₃

при ограничениях 12х₁ + 3х₂ + 6х₃ + 3х₄ = 9

8х₁ + х₂ – х₄ + 2х₅ = 10

3х₁ –х₆ = 0 х₁, … х₆  0

Тема: Искусственные переменные и М – метод.

№3.16. Рассмотрите систему ограничений:

-2х₁ + 3х₂ = 3 (1)

4х₁ + 5х₂  10 (2)

х₁ + 2х₂  5 (3)

6х₁ + 7х₂  3 (4)

4х₁ + 8х₂  5 (5)

Пусть х₁; х₂  0. С помощью подстановки искусственных переменных, используемой в М – методе, составьте начальное Z – уравнение для каждого из следующих случаев:

а) максимизировать Z = 5х₁ + 6х₂ при ограничениях (1), (3) и (4)

б) максимизироватьZ = 2х₁ – 7х₂ при ограничениях (1), (2), (4) и (5)

в) минимизировать Z = 3х₁ + 6х₂ при ограничениях (3), (4) и (5)

г) минимизировать Z = 4х₁ + 6х₂ при ограничениях (1), (2) и (5)

д) минимизировать Z = 3х₁ + 2х₂ при ограничениях (1) и (5)

№3.17. С помощью М – метода решите задачу ЛП, имеющую систему ограничений.

х₁ + х₂ +х₃ = 7

2х₁ – 5х₂ + х₃  10

х₁; х₂; х₃  0

и следующую целевую функцию:

а) максимизировать Z = 2х₁ + 3х₂ – 5х₃

б) минимизировать Z = 2х₁ + 3х₂ – 5х₃

в) максимизировать Z = х₁ + 2х₂ + х₃

г)минимизировать Z = 4х₁ – 8х₂ + 3х₃

№3.18. Рассмотрите следующую задачу: (на экзамен)

максимизировать Z = х₁ + 5х₂ + 3х₃

при ограничениях х₁ + 2х₂ + х₃ = 3

2х₁ – х ₂ = 4

х₁; х₂  0.

Пусть R соответствует искусственной переменной, вводимой в уравнение второго ограничения. Решите задачу, используя в начальном базисном решении переменные х₃ и R.

№3.19. Рассмотрите следующую задачу:

максимизировать Z = 2х₁ + 4х2 + 4х₃ – 3х₄

при ограничениях х₁ + х₂ + х₃ = 4

х₁ + 4х + х₄ = 8

х₁, … х₄  0

Найдите оптимальное решение, используя в начальном базисном решении переменные х₃ и х₄.

№3.20. Решите следующую задачу, используя в начальном допустимом базисном решении переменные х₃ и х₄.

минимизировать Z = 3х₁ + 2х₂ + 3х₃

при ограничениях х₁ +4 х₂ + х₃  7

2х₁ + х₂ + х₄  10

х₁, … х₄  0.

№3.21. Применительно к каждому из случаев, перечисленных в задаче №3.16., постройте целевую функцию для этапа I двухэтапного метода решения. (не рассматривали в лекциях).

Тема: Анализ модели на чувствительность.

№3.30. Рассмотрите следующую задачу ЛП, связанную с распределением ресурсов:

максимизировать Z = 3х₁ + 2х₂ (прибыль)

при ограничениях 4х₁ + 3х₂  12 (ресурс 1)

4х₁ + х²  8 (ресурс 2)

4х₁ – х₂  8 (ресурс 3)

х₁; х₂  0

С – Т, соответствует оптимальному решению задачи:

Базисные переменные	х1 х2 х3 х4 х5	Решение
Z	0 0 5/8 1/8 0	17/2
Х2 Х1 Х5	0 1 ½ -1/2 0 1 0 -1/8 3/8 0 0 0 1 -2 1	2 3/2 4

а) Определите статус каждого ресурса.

б) Определите ценность каждого ресурса.

в) Используя данные о ценности каждого ресурса, определите, запрос какого из них следует увеличить в первую очередь.

г) – Определите максимальный интервал изменения запасов ресурса 1, в пределах которого текущее решение остается допустимым.

д) – Выполните задание пп.(г) применительно к ресурсу 2.

е) – Для пп.(г) и (д) определите соответствующие изменения оптимальных значений Z.

ж) – Определите максимальный интервал изменения удельной прибыли для переменной х₁, в пределах которого полученное решение остается оптимальным.

з) – Выполните задание пп.(ж) применительно к переменной х₂.

№3.31. Рассмотрите следующую линейную оптимальную модель распределения ресурсов:

максимизировать Z = 2х₁ + 4х₂ (прибыль)

при ограничениях х₁ + 2х₂  5 (ресурс 1)

х₁ + х₂  4 (ресурс 2)

х₁; х₂  0

С – Т, соответствует оптимальному, имеет вид:

Базисные переменные	х1 х2 х3 х4	Решите
Z	0 0 2 0	10
Х2 Х4	½ 1 ½ 0 ½ 0 -1/2 1	5/2 3/2

Определите статус ресурса (дефицит, недефицит)

Лекция 10:

Линейное программирование: двойственность. Определение двойственной задачи. Соотношения двойственности.

Двойственная задача – эта вспомогательная задача ЛП, формулируемая с помощью определенных правил непосредственно из условий исходной, или прямой, задачи. В литературе по ЛП в большинстве случаев рассматриваются формулировки двойственной задачи, соответствующих различным формам прямой задачи, которые в свою очередь определяются типом ограничений, знаками переменных и направлением оптимизации ( максимизация или минимизация ). Опыт показывает, что на начальной стадии изучения теории ЛП детали различных формулировок двойственной задачи нередко затрудняют восприятие материала. Кроме того, практическое использование теории двойственности на самом деле и не требует знания деталей различных формулировок двойственной задачи.

Мы дадим обобщенную формулировку двойственной задачи ЛП, которая применила к любой форме представления прямой задачи. В основу такой формулировки положен тот факт, что использование СМ требует приведения любой задачи ЛП к стандартной форме. Так как все методы вычислений, основанные на соотношениях двойственности, предполагают непосредственное использование С – Т, формулировка двойственной задачи в соответствии со стандартной формой прямой задачи представленной достаточно логичной. Как будет показано ниже, при такой формулировке двойственной задачи автоматический учитываются знаки двойственных переменных, что в других случаях нередко вызывает недоразумения. Следует, однако, помнить, что приводимая ниже формулировка двойственной задачи является обобщенной в том смысле, что она применима ко всем формам прямой задачи. Прямая задача ЛП в стандартной форме записывается следующим образом:

Максимизировать n

или Z =  C_j X_j

минимизировать j=1

при ограничениях  a_ij x_j = b_i I = 1, 2 … m

j=1 x_j  0 j = 1, 2 … n

Заметим, что в состав n переменных х_j включаются также избыточные переменные. Чтобы сформулировать условия двойственной задачи, расположим коэффициенты, фигурирующие в условиях прямой задачи, так, как схематически показано в таблице:

Переменные прямой задачи

	х1 х2 … хj … хn
Правые части ограничений двойственной задачи	С1 С2 … Сj … Сn
Коэффициенты левых частей ограничений двойственной задачи	а11 а12 … а1j … а1m а21 а22 … а2j … а2m … … … … … … … … … … … … аm1 аm2 … amj … amn	b1 b2 … … bm	y1 y2 … … ym	Перемен- ные двойст- венной задачи

Из приведенной схемы следует, что двойственная задача получается путем симметричного структурного преобразования условий прямой задачи в соответствии со следующими правилами:

1. каждому ограничению прямой задачи соответствует переменная двойственной задачи;

2. каждой переменной прямой задачи соответствует ограничение двойственной задачи;

3. коэффициенты при некоторой переменной, фигурирующие в ограничениях прямой задачи, становятся коэффициентами левой части соответственно. Ограничения двойственной задачи, а коэффициент фигурирующий при той же переменной в выражении для целевой функции прямой задачи, становится постоянной правой части этого же ограничения двойственной задачи (см. н-р, заштрихованный столбец, соответствующих в таблице переменных х_j).

Из указанных правил построения двойственной задачи следует, что она имеет m переменных (y₁, y₂ … y_m) и n ограничений (соответствующие n переменным прямой задачи (х₁; х₂; … х_n).

Рассмотрим теперь, как формируются остальные условия двойственной задачи: направление оптимизации, ограничения и знаки двойственных переменных. Интерпретация по этим вопросам применительно к максимальной и минимальной целевым функциям задачи в стандартной форме представлена в таблице:

Прямая задача в стандартной форме*) Целевая функция.	Двойственная задача
	Целевая функция	Ограничения	Переменные
Максимизация минимизация	Минимизация максимизация	 	Не ограничены в знаке Не ограничены в знаке

^*) Все ограничения прямой задачи – равенства с неотрицательными правыми частями, а все переменные неотрицательные.

Напомним, что в стандартной формулировке прямой задачи все ограничения записываются в виде равенств (с неотрицательной правой частью), а все переменные неотрицательные. Поэтому, существенным различием прямых задач, записанных в стандартной форме, является только направление оптимизации.

Рассмотрим примеры построения двойственной задачи.

Пример №1. Прямая задача:

Максимизировать Z = 5х₁ + 12х₂ + 4х₃

при ограничениях х₁ + 2х₂ + х₃  10

2х₁ – х₂ + 3х₃ = 8

х₁; х₂; х₃  0

Прямая задача в стандартной форме:

Максимизировать Z = 5х₁ + 12х₂ + 4х₃ + 0х₄

при ограничениях х₁ + 2х₂ + х₃ + х₄ = 10

2х₁ – х₂ + 3х₃ + 0х₄ = 8

х₁ … х₄  0.

Заметим, что х₄ – остаточная переменная, введенная в 1-ое ограничение. Поэтому коэффициенты, фигурирующие при этой переменной в целевой функции и во 2-ом ограничении = 0.

Двойственная задача:

Минимизировать  = 10y₁ + 8y₂ при ограничениях

Х₁: у₁ + 2х₂  5

Х₂: 2у₁ – у₂  12

Х₃: у₁ + 3у₂  4

Х₄: у₁ + 0у₂  0 (означает, что у₁  0)

у₁; у₂ не ограничены в знаке

Следует отметить, что у₁  0 является более жестким, чем условие неограничения у₁ в знаке. Поэтому при исключении этой избыточности ограничений двойственная задача формулируется следующим образом:

Минимизировать  = 10у₁ + 8у₂

При ограничениях у₁ + 2у₂  5

2у₁ – у₂  12

у₁ + 3у₂  4,

у₁  0; у₂ не ограничена в знаке.

Пример №2. Прямая задача:

Минимизировать Z = 5х₁ – 2х₂ при ограничениях

-х₁ + х₂  -3

2х₁ + 3х₂  5

х₁; х₂  0.

Прямая задача в стандартной форме:

Минимизировать Z = 5х₁ – 2х₂

При ограничениях х₁ – х₂ + х₃ = 5

х₁ … х₄  0.

Двойственная задача:

Максимизировать  = 3у₁ + 5у₂

При ограничениях у₁ + 2у  5

-у₁ + 3у₂  -2

у₁  0; у₂  0

у₁; у₂ не ограничены в знаке

(избыточные ограничения)

Упражнение к примеру №2. Как изменяются условия сформулированной выше двойственной задачи, если знак неравенства () во втором ограничении прямой задачи изменится на противопол. ()?

Ответ: Ограничение у₂  0 примет вид у₂  0.

Пример № 3. Прямая задача:

Максимизировать Z = 5х₁ + 6х₂

При ограничениях х₁ + 2х₂ = 5

-х₁ + 5х₂  3

4х₁ + 7х₂  8

х₁ не ограничена в знаке, х₂  0.

Прямая задача в стандартной форме:

Пусть х₁ = х₁¹ – х₁¹¹ где х₁¹, х₁¹¹  0. Стандартная формулировка прямой задачи при использовании такой подстановки имеет вид:

Максимизировать х = 5х₁¹ – 5х₁¹¹ + 6х₂

При ограничениях х₁¹ – х₁¹¹ + 2х₂ = 5

-х₁¹ + х₁¹¹ + 5х₂ – х₃ = 3

4х₁¹ – 4х₁¹¹ + 7х₂ + х₄ = 8

х₁¹, х₁¹¹, х₂, х₃, х₄  0.

Двойственная задача

Минимизировать  = 5у₁ + 3у₂ + 8у₃

При ограничениях у₁ – у₂ 4у₃  5 

 означает, что у₁ – у₂ + 4у₃ = 5

-у₁ + у₂ – 4у₃  -5 

2у₁ + 5у₂ + 7у₃  6

-у₂  0 (означает, что у₂  0 )

у₃  0

у₁ не ограничена в знаке.

у₂; у₃ не ограничены в знаке (избыточные условия)

Заметим, что 1-ое и 2-ое ограничения двойственной задачи можно (но не обязательно) заменить одним ограничением в виде равенства у₁ – у₂ + 4у₃ = 5. Такая замена возможна всякий раз, когда переменная прямой задачи не ограничена в знаке, то есть неограниченность в знаке переменной прямой задачи всегда обуславливает появления ограничения двойственной задачи в виде равенства (а не неравенства) как при максимизации, так и минимизации целевой функции прямой задачи.

Задачи.

№4.1 Для каждой из приведенных ниже задач сформулируйте двойственную задачу:

а) максимизировать Z = -5х₁ + 2х₂

при ограничениях -х₁ + х₂  - 3

2х₁ + 3х₂  5

х₁ х₂  0

б) минимизировать Z = 6х₁ + 3х₂

при ограничениях 6х₁ – 3х₂ + х₃  2

3х₁ + 4х₂ + х₃  5

х₁ х₂ х₃  0

в) максимизировать Z = 5х₁ + 6х₂

при ограничениях х₁ + 2х₂ = 5

-х₁ + 5х₂  3

х₁ не ограничена в знаке х₂  0

г) минимизировать Z = 3х₁ + 4х₂ + 6х₃

при ограничениях х₁ + х₂  10

х₁ х₃  0 х₂  0

д) максимизировать Z = х₁ + х₂

при ограничениях 2х₁ + х₂ = 5

3х₁ – х₂ = 6

х₁; х₂ не ограничены в знаке.

№ 4.2. Рассмотрим следующую задачу:

минимизировать Z = х₁ + 2х₂ – 3х₃

при ограничениях -х₁ – х₂ + х₃ = 5

12х₁ – 9х₂ + 9х₃  8

х₁; х₂; х₃  0

Для решения данной задачи СМ-ом в каждое из 2^х ограничений необходимо ввести искусственные переменные. Покажите, что двойственные задачи, получаемые из прямой задачи в стандартной форме до и после введения искусственных переменных тождественны. Искусственным переменным могут соответствовать только избыточные ограничения двойственной задачи.

№ 4.3. Решите задачу № 4.2. заменив целевую функцию вида:

максимизировать Z = 5х₁ – 6х₂ + 7х₃

Лекция 11:

Определение транспортной модели и ее применение.

Транспортная модель используется при разработке плана перевозок одного вида продукции из нескольких пунктов отправления в пункты назначения. При построении модели используются:

1) величины, характеризующие объём производства в каждом пункте назначения;

2. стоимость перевозки единицы продукции из каждого исходного пункта в каждый пункт назначения.

Поскольку рассмотрим только один вид продукции, потребности продукта назначения (п.н.) могут удовлетворяться за счет нескольких исходных пунктов. Цель построения модели состоит в определении количества продукции, которое следует перевезти из каждого исходного пункта в каждый п.н., с тем чтобы общие транспортные расходы были min.

Основное предположение, используемое при построении модели, состоит в том, что величина транспортных расходов на каждом маршруте прямо пропорциональна объему перевозимой продукции. Единицами измерения объема перевозимой продукции м.б. н-р., одна стальная балка, направляемая на строительство моста, или грузовик. В любом случае единица производства и потребления должны соответствовать принятым определением единицам перевозимой продукции.

И сходные пункты. Пункты назначения.

а ₁  1 С₁₁ : Х₁₁

1 в₁

о бъем производства спрос

а ₂ 2 2 в₂

… …

… …

а _m  m n в_n

C_mn : X_mn

Рис 1.

На рис. 1. изображена транспортная модель (ТМ) в виде сети с m исходными пунктами и n пунктами назначения. Исходным пунктом и пунктом назначения соответствуют вершины. Дуга, соединяющая и.п. с п.н., представляют маршрут, по которому перевозится продукция. Количество продукции, производимой в пункте i, обозначено через а_i , а количество продукции, потребляемой в пункте j, - через в_j.

C_ij – стоимость перевозки единицы продукции из i в j.

Пусть х_ij – количество продукции, перевозимой из исходного пункта i в пункт назначения j; тогда задача ЛП транспортного типа в общем виде формулируются следующим образом:

m n

Минимизировать Z =   C_ij X_ij

i=1 j=1

при ограничениях

n

• X_ij  a_i; I = 1,2,…m

j=1 m

 X_ij  b_j, j = 1,2,…n

i=1

x_ij  0 для всех i и j.

Первая группа ограничений указывает, что суммарный объем перевозок продукции из некоторого исходного пункта не может превышать произведенного количества этой продукции; вторая группа ограничений требует, чтобы суммарные перевозки продукции в некоторый пункт потребления полностью удовлетворили спрос на эту продукцию.

Из представленной модели видно, что суммарный объем производства в исходных пунктах а_i не должны быть меньше суммарного спроса в пунктах назначения b_j Если суммарный объем производства равен суммарному спросу (а_i = b_j), то модель называется сбалансированной транспортной моделью. Она отличается от вышеприведенной модели лишь тем, что все ограничения превращаются в равенства, то есть

Х_ij = a_i I = 1,2,…m

X_ij = b_j j = 1,2,…n

В реальных условиях не всегда объем производства равен спросу или превосходит его. Однако, ТМ всегда можно сбалансировать.

Лекция 12:

Решение транспортной задачи. Метод решения транспортной задачи.

Основные шаги алгоритма.

Шаг 1. Найти начальное допустимое решение.

Шаг 2. Выделить из числа небазисных переменных вводимую в базис. Если все небазисные переменные удовлетворяют условию оптимальности (СМ), закончить вычисления; в противном случае перейти к шагу 3.

Шаг 3. Выбрать выводимую из базиса переменную (используя условие допустимости) из числа переменных текущего базиса; затем найти новое базисное решение. Вернуться к шагу 2.

Рассмотрим алгоритм подробнее. Для пояснения воспользуемся задачей, соответствующей таблице 1. Стоимость перевозки единицы продукции С_ij дана в долларах. Объем производства и величины спроса представляются в количествах изделий.

Таблица 1

Исходные пункты	П у н к т ы н а з н а ч е н и я				Объем производства
	1 10	2 0	3 20	4 11
1	Х11	Х12	Х13	Х14	15
2	12 Х 0 21	7 Х 14 22	9 Х 16 23	20 Х 18 24	25
3	Х31	Х32	Х33	Х34	5
	5	15	15	10
	С п р о с

Определение начального решения.

Согласно общему определению ТМ, необходимо, чтобы а_i = b_j. Из этого требования следует, что одно уравнение оказывается зависимым, то есть ТМ содержит только m + n – 1 независимых уравнений.

Таким образом, как и в СМ, начальное базисное допустимое решение должно иметь m + n – 1 базисную переменную.

Обычно, если ТМ представлена в виде С-Т, для получения начального базисного решения следует использовать искусственные переменные. Однако, если построить транспортную таблицу, начальное базисное допустимое решение легко получить непосредственно из нее. Для этой цели опишем процедуру, основанную на так называемом правиле северо-западного угла. Две другие процедуры, называемые методом минимальной стоимости и приближенный алгоритмом Фогеля обычно дают лучшие начальное решение, обеспечивающее меньшее значение целевой функции.

Следуя правилу северо-западного угла, начинают с того, что приписывают переменной х₁₁ (Расположить в северо-западном углу таблицы) максимальное значение, допустимое ограничениями на спрос и объем производства. После этого вычерчивают столбец (или строку), фиксируя этим, что остальные переменные вычеркнутого столбца (строки) полагаются равными 0.

Если ограничения, представляемые столбцом и строкой, выполняются одновременно, то можно вычеркнуть либо столбец, либо строку. После того как спрос и объем производства во всех не вычеркнутых строках и столбцах приведены в соответствие с установленным значением переменной, максимально допустимое значение приписывается 1-му не вычеркнутому элементу нового столбца (строки). Процесс завершается не вычеркнутой в точности одна строка (или один столбец) .

Применим описанную процедуру к примеру табл. 1.

1. х₁₁ = 5, столбец 1 вычеркивается. Тем самым в 1-ом столбце нельзя больше производить никаких операций. На строку 1 теперь приходится 10 единиц.

2. х₁₂ = 10, строка 1 вычеркивается, а на долю столбца 2 остается 5 единиц.

3. х₂₂ = 5, столбец 2 вычеркивается, а в строке 2 остается 20 единиц.

4. х₂₃ = 15, столбец 3 вычеркивается, в столбце 4 остается 5 единиц.

5. х₂₄ = 5, строка 2 вычеркивается, в столбце 4 остается 5 единиц.

6. х₃₄ = 5, вычеркивается строка 3 или столбец 4. Поскольку остается только один столбец или только одна строка, процесс заканчивается. Полученное базисное решение приведено в табл. 2.

	1	2	3	4
1	5	10			15
2		5	15	5	25
3				5	5
	5	15	15	10

Базисные переменные принимают значения: х₁₁ = 5; х₁₂ = 10; х₂₂ = 5;

х₂₃ = 15; х₂₄ = 5; х₃₄ = 5.

Остальные переменные небазисные, со значениями = 0. Соответствующие транспортные расходы равны 5*10+10*0+5*7+15*9+5*20+5*18=410 долл.

Если одновременно и столбец, и строка удовлетворяют ограничениям, очередная переменная, включаемая, в базисное решение, обязательно имеет нулевое значение. Табл. 3 иллюстрирует эту ситуацию.

	1	2	3	4
1	5	5			1 0 5
2		5	0		5 0
3			8	7	15
			8	7

Столбец 2 и строка 2 одновременно приводят к выполнению соответст. ограничений. Если вычеркивается столбец 2, то на следующем шаге переменная х₂₃ становится базисной с нулевым значением, поскольку величина предложения в строке 2 равна 0. (табл.3).

Если вычерчивается строка 2, то х₃₂ становится нулевой базисной переменной.

Начальные решения в табл. 2 и 3 содержат необходимое количество базисных переменных, равное m + n – 1 = 6. Использование правила северо-западного угла всегда приводит к нужному числу базисных переменных.

Нахождение вводимой в базис переменной

(метод потенциалов).

Вводимую в базис переменную находят, используя условия оптимальности СМ. Вычисление коэффициентов целевой функции основано на соотношениях между прямой и двойственной з-ми. Сначала рассмотрим, как реализуется метод, а затем дадим строгое объяснение вычислительных процедур на основе теории двойственности. Для определения вводимой в базис переменной можно использовать и другой метод, называемый методом «опорных элементов». Хотя вычислительные процедуры в рамках этих методов полностью эквивалентны, метод опорных элементов кажется совершенно непохожим на СМ.

В методе потенциалов строке i и столбцу j транспортные таблицы ставятся в соответствии числа U_i и V_j. Для каждой базисной переменной Х_ij текущего решения потенциалы U_i и V_j должны удовлетворять уравнению

U_i + V_j = C_ij

Эти уравнения приводят к системе, состоящей из m + n – 1 уравнений (поскольку всего имеется m + n – 1 базисных переменных), в которых фигурируют m + n неизвестных. Значения потенциалов можно определить из этой системы, придавая одному из них произвольное значение (обычно U₁ полагается равным нулю) и затем решая систему из m + n – 1 уравнений относительно m + n – 1 остальных потенциалов. Как только решение получено, оценки для небазисных переменных Х_pg определяются в соответствии с соотношением

С _pq = U_p + V_q – C_pq.

( эти величины не зависят от выбора значения U₁ ). После этого для включения в базис выбирается небазисная переменная, имеющая самую большую положительную оценку C_pq (сравните с условием оптимальности СМ при решении задачи на отыскание минимума).

Если эту процедуру применить к небазисным переменным табл. 2 (текущее решение), то уравн1ения, связанные с базисными переменными, будут иметь вид:

X₁₁ : U₁ + V₁ = C₁₁ = 10; U₁ = 0; V₁ = 10

X₁₂ : U₁ + V₂ = C₁₂ = 0; U₁ = 0; V₂ = 0

X₂₂ : U₂ + V₂ = C₂₂ = 7; V₂ = 0; U₂ = 7

X₂₃ : U₂ + V₃ = C₂₃ = 9; U₂ = 7; V₃ = 9 – 7 = 2

X₂₄ : U₂ + V₄ = C₂₄ = 20; U₂ = 7; V₄ = 20 – 7 = 13

X₃₄ : U₃ + V₄ = C₃₄ = 18; V₄ = 13; U₃ = 18 – 13 = 5

Полагая U₁ = 0, получим значения потенциалов V₁ = 10; V₂ = 0 ; V₃ = 9 –7 = 2; V₄ = 20 – 7 = 13; U₃ = 18 – 13 = 5. Оценки для небазисных переменных определяется следующим образом:

X ₁₃ : C₁₃ = U₁ + V₃ – C₁₃ = 0 + 2 – 20 = -18

X ₁₄ : C₁₄ = U₁ + V4 – C₁₄ = 0 + 13 – 11 = 2

X₂₁ : C₂₁ = U₂ + V₁ – C₂₁ = 7 + 10 – 12 = 5

X ₃₁ : C₃₁ = U₃ + V₁ – C₃₁ = 5 + 10 – 0 = 15

X ₃₂ : C₃₂ = U₃ + V₂ – C₃₂ = 5 + 0 – 14 = -9

X ₃₃ : C₃₃ = U₃ + V₃ – C₃₃ = 5 + 2 – 16 = -9

Поскольку переменная Х₃₁ имеет максимальный положительный оценку С_pq, она и выбирается в качестве вводимой в базис.

Уравнения U_i + V_j = C_ij, используемые для нахождения потенциалов, имеют настолько простую структуру, что на самом деле их нужно записывать в явном виде. Обычно гораздо проще определить потенциалы непосредственно из транспортной таблицы, заметив, что U_i строки i и V_j столбца j прибавляются к C_ij, если на пересечении строки i и столбца j находится базисная переменная X_ij. Определив U_i и V_j можно вычислить C_pq для всех небазисных переменных X_pq, прибавляя U_p строки p к V_q столбца q и затем вычитая величину C_pq, стоящую на пересечении строки p и столбца q.

Нахождение переменной, выводимой из базиса

(построение цикла).

Этот шаг эквивалентен использованию условия допустимости в СМ. Вместе с тем, поскольку все коэффициенты в ограничениях транспортной задачи равны либо нулю, либо 1, отношения, используемые при проверке условия допустимости, всегда будут иметь знаменатель, равный 1. Поэтому значения базисных переменных сразу же дают соответствие отношения.

Для определения min отношения построим замкнутый цикл, соответствующий вводимой переменной ( Х₃₁ на данной итерации). Цикл начинается и заканчивается выбранной переменной. Он состоит из последовательности горизонтальных и вертикальных (связанных) отрезков, концами которых должны быть базисные переменные (за исключением тех концов, которые относятся к вводимой в базис переменной). Это означает, что каждая ячейка, стоящая на изломе цикла, должна содержать базисную переменную. Табл. 4 иллюстрирует цикл, соответствующий вводимой переменной х₃₁, для базисного решения из табл. 2.

Таблица 4.

	1	2	3	4
1	5 10	10 0	20	11	15
2	12	5 7	15 9	5 20	25
3	Х31 0	14	16	5 18	5
	5	15	15	10

Э тот цикл можно выразить при помощи базисных переменных следующим образом: Х₃₁  Х₁₁  Х₁₂  Х₂₂  Х₂₄  Х₃₄  Х₃₁. Несущественно, в каком направлении (по часовой или против часовой стрелки) происходит обход цикла. Заметим, что для каждого решения и соответствует небазисной переменной можно построить лишь один цикл. Из табл. 4. видно, что если значение Х₃₁ (вводимой в базис переменной) увеличится на единицу, для сохранения допустимости решения значения базисных переменных, стоящих на изломах Х₃₁ цикла, необходимо скорректировать следующим образом: уменьшить Х₁₁ на единицу, увеличить Х₁₂ на единицу, уменьшить Х₂₂ на единицу, Х₂₄ на единицу и, наконец, Х₃₄ на единицу. Этот процесс обозначается знаками + и - в соответствии местах таблицы 4. Введенные изменения не нарушают ограничений, накладываемых на объем производства и спрос.

П еременная, выводимая из базиса, выбирается из находящихся на изломах цикла переменных, значения которых уменьшаются при увеличении Х₃₁. Они располагаются в таблице 4. в местах, помеченных знаком -. Из таблицы 4. следует, что Х₁₁, Х₂₂, Х₃₄ – базисные переменные, уменьшающиеся с ростом Х₃₁. Выводимой из базиса переменной становится та, которая имеет наименьшее значение, поскольку именно она раньше всех достигнет нуля, и любое дальнейшее уменьшение делает ее отрицательной (сравните с условием допустимости в СМ, где исключаемая переменная определяется min отношением). В данном примере три - - переменных Х₁₁; Х₂₂ и Х₃₄ имеет одно и то же значение (=5); в этом случае любую из них можно исключить из базиса. Пусть выбрана переменная Х₃₄; тогда значение Х₃₁ становится равным 5, а переменные, находящиеся на изломах цикла (базисные), соответствующим образом корректируются (то есть каждая из них увеличивается или уменьшается на 5 единиц в зависимости от знака + или - ) Новое решение приведено в таблице 5. Соответствующая стоимость – 0 * 10 + 15 * 0 + 0 * 7 + 15 * 9 + 10 * 20 + 5 * 0 = 335 дол. Полученная стоимость отключается от стоимости, соответствующему начальному решению (табл. 2.), на 410 – 335 = 75 долл, то есть на величину, приписанную переменной Х₃₁ = (5) и умножаемую на С₃₁ (=5)

Т аблица 5.

	1	2	3	4
1	0 10	15 0	20	11	15
2	12	0 7	15 9	10 20	25
3	5 0	14	16	18	5
	5	15	15	10

Базисное решение в таблице 5 вырожденное, поскольку базисные переменные Х₁₁ и Х₂₂ = 0. Однако вырожденность не требует никаких дополнительных мер предосторожности; с нулевыми базисными переменными оперируют точно так же, как с переменными имеющими положительные значения.

Оптимальность нового базисного решения (табл. 5.) проверяется вычислением новых потенциалов (табл.6). Величины С_pq указывается в юго-западном углу каждого небазисного элемента. Таблица 6.

	V1 = 10	V2 = 0	V3 = 2	V4 = 13
U1 = 0	0 10	15 0	20 - 18	11 +2	15
U 2 = 7	Х21 12 + 5	0 7	15 9	10 20	25
U3 = -10	5 0	14 - 24	16 - 24	18 -15	5
	5	15	15	10

Б азисная переменная Х₂₁, имеющая наибольшую положительную оценку C_pq, войдет в решение. Замкнутый цикл, соответствующий Х₂₁, показывает, что переменной, исключаемой из базиса, может быть как Х₁₁, так и Х₂₂. Выберем в качестве такой переменной Х₁₁. В таблице 7 представлено новое базисное решение, полученное из таблицы 6 (Х₂₁ вводится в базис, а Х₁₁ исключается).

Таблица 7.

	V1 = 5	V2 = 0	V3 = 2	V4 = 13
U 1 = 0	10 -5	15 0	20 - 18	Х14 11 + 2	10
U2 = 7	1 2	0 7	15 9	10 20	25
U3 = -5	5 0	14 -19	16 - 19	18 -10	5
	5	15	15	10

Значения U_i; V_j и C_pq вычисляем заново. В таблице 7 переменной, вводимой в базис, и исключаемой переменной является Х₁₄ и Х₂₄ соответственно. Осуществив соответствующие изменения в таблице 7 можно получить новое решение, представленной в таблице 8. Поскольку все С_pq в таблице 8 неположительные, полученные решение оптимально (сравните с условием оптимальности СМ при решение задачи на отыскание минимума.

Таблица 8.

	V1 = 5	V2 = 0	V3 = 2	V4 = 11
U 1 = 0	10 -5	15 0	20 - 18	Х14 11	10
U2 = 7	12	10 7	15 9	20 -2	25
U3 = -5	5 0	14 -19	16 - 19	18 -12	5
	5	15	15	10

Оптимальное решение формулируется следующим образом. Перевезти 5 единиц из пункта производства 1 в пункт потребления 2, заплатив 5 * 0 = 0 долл., 10 единиц из 1 в 4 за 10 * 11 = 110 долл., 15 единиц из 2 в 3 за 15 * 9 = 135 долл. И 5 единиц из 3 в 1 за 5 * 0 = 0 долл. Суммарные транспортные расходы составляют 135 долл.

ЛЕКЦИЯ 13:

Улучшенное начальное решение. Приближенный метод Фогеля (ПМФ).

Метод северо-западного угла, не обязательно дает «хорошее» начальное решение для транспортной задачи. Опишем две процедуры, обеспечивающие получение начального решения путем выбора «дешевых» маршрутов.

Метод наименьшей стоимости.

Вычисления проводятся следующим образом. Выбирается переменная, которой соответствует наименьшая стоимость во всей таблице, и ей придается возможно большее значение. (Если таких переменных несколько, то берется любая из них). Вычеркивается соответствующий столбец или строка. Если ограничения по столбцу и строке выполняются одновременно, то, как и в методе северо-западного угла, вычеркивается либо столбец, либо строка. После вычисления новых значений спроса и объема производства для всех невычеркнутых строк и столбцов процесс повторяется при возможно большем значении той переменной, которой соответствует минимальная стоимость среди невычеркнутых. Процедура завершается, когда остается одна строка или один столбец. Для иллюстрации применения метода наименьшей стоимости воспользуемся транспортной задачей из таблицы 1.

Таблица (1а).

	1	2	3	4
1	0 10	15 0	20	0 11	15
2	12	0 7	15 9	10 20	25
3	5 0	14	16	18	5
	5	15	15	10

В таблице (1а) приведено начальное решение, полученное следующим образом: Х₁₂ и Х₃₁ – переменные , которым соответствуют минимальные стоимости (С₁₂ = С₃₁ = 0). Выберем произвольно Х₁₂. Соответственно значения спроса и объема производства определяют Х₁₂ = 15, то есть и по строке, и по столбцу ограничения выполняются. После вычерчивания столбца 2 объем производства в строке 1 остается равным нулю. Теперь среди оставшихся элементов минимальная стоимость соответствует переменной Х₃₁. Значения Х₃₁ = 5 удовлетворяет ограничениям и по столбцу 1, и по строке 3. После вычеркивания строки 3 оставшийся спрос в столбце 1 = 0. Наименьший невычеркнутый элемент – С₂₃ = 9.

Ограничения на спрос и объем производства определяют Х₂₃ = 15, что приводит к вычеркиванию столбца 3, а значения объема производства в строке 2 становится =10. Наименьшая невычеркнутая стоимость С₁₁ = 10. Поскольку остаток объема производства в строке 1 и остаток спроса в столбце 1 = 0, Х₁₁= 0.

При вычеркивании столбца 1 « остаток» объема производства в строке 1= 0. Остальные базисные переменные имеют значения Х₁₄ = 0 и Х₂₄ = 10. Суммарные затраты, соответствуют этому решению равны 0 * 10 + 15 * 0 + 0 * 11 + 15 *- 9 + 10 * 20 + 5 * 0 = 335 долл., что лучше результата, полученного при использовании северо-западного угла.

Приближенный метод Фогеля ( ПМФ).

Этот метод является эвристическим и обычно приводит к лучшему начальному решению, чем два описанных выше. На самом деле ПМФ часто дает оптимальное или близкое к оптимальному начальное решение.

Алгоритм состоит из следующих шагов.

Шаг 1. Вычислить штраф для каждой строки (столбца), вычитая наименьший элемент этой строки (столбца) из следующего за ним по величине элемента той же строки (столбца).

Шаг 2. Отметить строку или столбец с самым большим штрафом, если таких несколько, выбрать среди них любую строку или любой столбец. В отмеченной строке или столбце выбрать переменную с самой низкой стоимостью и придать ей наибольшее возможное значение. Скорректировать объем производства и спрос и вычеркнуть строку или столбец, соответственному выполненному ограничению. Если ограничения по строке и столбцу выполняются одновременно, то вычеркнуть либо строку, либо столбец, а оставшемуся столбцу (строке) приписать нулевой спрос (объем производства). Строка (или столбец) с нулевым объемом производства (или спросом) не используются в дальнейших вычислениях (на шаге 3).

Шаг 3. (а) Если невычеркнутой остается в точности одна строка или один столбец, то закончить вычисления.

(б). Если невычеркнутой только одна строка (столбец) с положительным объемом производства (спросом), найти базисные переменные в этой строке (столбце), используя метод наименьшей стоимости.

(в). если всем невычеркнутым строкам и столбцам соответствуют нулевые объемы производства и величины спроса, найти нулевые базисные переменные, используя метод наименьшей стоимости.

(г). В других случаях вычисляют новые значения штрафов для невычеркнутых строк и столбцов и перейти к шагу 2. (следует отметить, что строки и столбцы с нулевыми значениями объема производства и спроса не должны использоваться при вычислении этих штрафов). Решим задачу, соответствующую таблице 1, при помощи ПМФ. Таблица 1.

П ункты назначения.

Исходные пункты	1	2	3	4	Объем производства
1	Х11 10	Х12 0	Х13 20	Х14 11	15
2	Х21 12	Х22 7	Х23 9	Х24 20	25
3	Х31 0	Х32 14	Х33 16	Х34 18	5
Спрос	5	15	15	5

Таблица 2 содержит первый набор штрафов для строк и столбцов. Поскольку строка 3 имеет наибольший штраф ( = 14) и С₃₁ = 0, является наименьшим коэффициентом стоимости в этой строке, переменной Х₃₁ приписывается значение 5. Ограничения по строке 3 и столбцу 1 выполняются одновременно. Пусть вычеркивается столбец 1. Остаток объема производства для строки 3 = 0.

Таблица 2.

	1	2	3	4	Штрафы для строк
1	10	0	20	11	15 10
2	12	7	9	20	25 2
3	5 0	14	16	18	5 14
Штрафы для столбцов	5 10	15 7	15 7	10 7

Таблица 3 содержит новый набор штрафов, полученный после вычеркивания столбца, в таблице 2 ( Следует отметить, что строка 3 с нулевым объемом производства не используется при вычислении штрафов).

Таблица 3.

	1	2	3	4	Штрафы для строк
1	10	0	20	11	15 11 11
2	12	7	9	20	2 5 10 2 13
3	5 0				5 0 - -
Штрафы для столбцов	5 -	15 7 7 0	1 5 11 - -	10 9 9 11

Строке 1 и столбцу 3 соответствуют одинаковые штрафы. При выборе столбца 3 переменная Х₂₃ принимает значение 15, в результате чего столбец 3 вычеркивается, а объем производства в строке 2 становится равным 10.

Последовательное применение ПМФ дает Х₂₂ = 10 (вычеркнуть строку 1) и Х₃₄ = 0 (Проверьте!) Суммарные затраты равны 315 долл.

Таким образом, полученное решение оказалось оптимальным.

Данный вариант ПМФ не включает правила выбора из одинаковых штрафов. Однако тот или иной выбор из одинаковых штрафов может оказать серьезное влияние на получение хорошего начального решения.

Например, если в таблице 3 вместо столбца 3 выбрать строку, то получится худшее начальное решение. (Покажете, что при этом будет найдено решение Х₁₂ = 15; Х₂₃ = 15; Х₂₄ = 10; Х₃₁ = 5. Суммарные затраты составят 335 долл.)

Упражнение: Повторите решение задачи, используя ПМФ и заменяя значение С₁₂ на 2 (вместо 0). При одновременном выполнении ограничений по строке и столбцу всегда вычеркивайте строку.

Ответ: Последовательность нахождения значений переменных дает Х₃₁ = 5 Х₂₃ = 15, Х₂₂ = 10 Х₁₄ = 10 Х₁₂ = 5 Х₁₁ = 0.

МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ

Задача управления запасами возникает, когда необходимо создать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени (конечном или бесконечном). Для обеспечения непрерывного и эффективного функционирования практически любой организации необходимо создание запасов.

91