3.4. Распределения биноминальное, пуассона и релея

Биноминальное распределение. Распределение случайной величины называется биноминальным, если она может принимать целые положительные значения 0, 1, 2, ... п с вероятностями

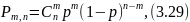
где 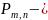вероятность того, что случайная величина примет значение т (т = 0, 1, 2, …п) из п возможных;

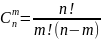
число сочетании из п по т;

p – вероятность рассматриваемого события (например, вероятность безотказной работы); 1– p =q — дополнение до вероятности полной группы событий (в принятом случае — вероятность отказа).

Математическое ожидание и дисперсию случайной величины, распределенной по биноминальному закону, можно записать так:

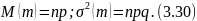
При больших п биноминальное распределение становится близким к нормальному с параметрами (3.22). Биноминальное распределение используется в данной работе при изучении задач резервирования.

Распределение Пуассона. Случайная величинах, принимающая только целые и положительные значения, подчиняется распределению Пуассона, если вероятность того, что она принимает значение х, определяется уравнением

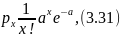
Математическое ожидание и дисперсия распределения:

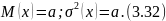
Если а = nλt, где п—число однотипных изделий; λ — интенсивность отказов, то (3.31) дает вероятность того, что число отказов за время t будет равно х.

Если число отказов х = 0, то из (3.31) следует вероятность безотказной работы

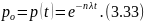
Характер изменения вероятност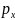и появления ровно х событий в зависимости от значения параметра а приведен на рис. 3.4. Для наглядности дискретные точки при данном значении а соединены отрезками прямых линий.

Распределение Пуассона широко используется при оценке случайного числа отказов восстанавливаемых изделий в период приработки, при расчетах количества запасных изделий (ЗИП) и др.

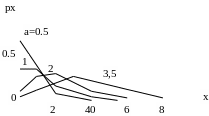
Рис. 3.4. Вероятности появления ровно х событий при разных значениях параметра а распределения Пуассона

Распределение Релея. Плотность вероятности распределений Релея случайной величины Т имеет вид:

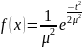
где μ — мода распределения.

Модой случайной величины называется ее наиболее вероятное значение, т. е. такое, при котором плотность вероятности максимальна.

Рис. 3.5. Показатели надежности при распределении Релея: a) λ(t), f(t); б)-p(t)

Вероятность безотказной работы

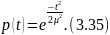
Интенсивность отказов

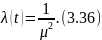
Математическое ожидание случайной величины

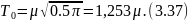
Дисперсия

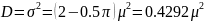
Зависимости f(t), λ(t), p(t) для случая распределения Релея приведены на рис. 3.5.

3.5. Равномерная плотность распределения

При равномерной плотности распределения (рис. 3.6) случайная величина с равной вероятностью расположена в любой точке и рсзкаа-6.

] la рисунке точкой h обозначена середина отрезка. Плотность вероятности определяется как

.1

О при JC< h-1; ^ - '

' (3.39)

1/2/при/г+ I.

Математическое ожидание

a + b ,

х_т=—— = Л . (3.40)

Дисперсия

2 2

Я = -^^- = у = 0,3333/2; (3.41)

Вероятность попадания в интервал d-g.

p(d<x<g)=^-^-. * (3.42)

о —a

Для случая характеристик надежности: а = О, 6 = t_x\

F(x)=\/t_x при t<t_x> » j (3.43) 0 при t > t

/>(/)=— = !--; ' (3.44)

MO ti"t

Соответствующие показатели надежности приведены на рис. 3.7.

72