Лекция 3

§ 9. Деревья и их свойства.

Деревья, как связные графы с минимальным числом ребер были открыты во второй половине XIX века разными учеными независимо друг от друга. В Германии Г. Кирхгоф открыл деревья и применил их к исследованию электрических цепей. В Англии А. Кэли открыл деревья, перечисляя изомеры углеводородов, а во Франции К. Жордан ввел деревья для описания математических объектов.

Деревом называется всякий связный граф, не имеющий циклов. Любой граф без циклов называется ациклическим или лесом. Таким образом, лес  объединение нескольких деревьев. На рис. 9.1 изображен лес из шести неизоморфных деревьев порядка 6.

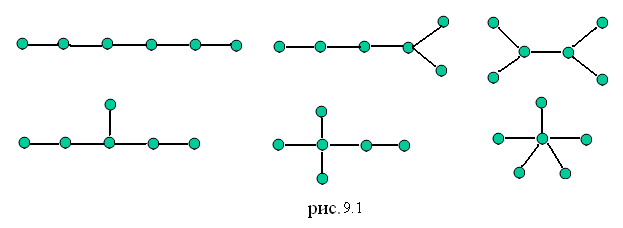
Всякое ребро в дереве (и в лесе) по теореме 1 из § 8 является мостом.

Существует несколько вариантов определения дерева.

Теорема 9.1 Для (n,m)графа G следующие утверждения эквивалентны:

1. G  дерево, (т.е. связный ациклический граф);

2. G  связный граф, и m = n1;

3. G  ациклический граф, и m = n1;

4. G  граф, в котором любые две несовпадающие вершины соединены единственной цепью;

5. G  ациклический граф со свойством: если любые две несмежные вершины соединить ребром е, то граф G + е содержит единственный цикл.

Из (1) следует (2), т.е. в дереве m = n1.

Доказательство индукцией по n.

При n = 1 утверждение очевидно: m = 0 = n1. Пусть для графов порядка <n равенство доказано. Докажем для графа G, у которого порядок равен n. Удалим из G одно ребро е, тогда по теореме 2 из § 8 граф Ge имеет 2 компоненты Т₁ и Т₂, каждая из которых является деревом. Пусть дерево Т1  (n₁, m₁)граф, Т2  (n₂, m₂)граф. Так как n₁ < n и n₂ < n , то по индуктивному предположению выполняются равенства: m₁=n₁1 и m₂=n₂1. Тогда получаем: m = m₁+ m₂ + 1 = ( n₁1)+( n₂1)+1 = (n₁+ n₂)1 = n1.

Докажем, что из (2) следует (3). Дано: G  связный граф, m = n1.

Доказать: G  ациклический, m = n1. Нужно доказать только, что G  граф без циклов.

Предположим противное: пусть в G есть цикл С, ребро е  С. Тогда по теореме 1 из § 8 граф Ge связный, и m = n  2.

По теореме 2 из § 8 nk ≤ m. Но k = 1 (граф Ge связный), поэтому n1 ≤ m =n2, т.е. n1 ≤ n2, получаем противоречие.

Докажем, что из (3) следует (4). Дано: G  ациклический граф и m = n1.

Докажем сначала, что G  связен. Пусть k  число компонент графа G, каждая компонента T_i  (n_i, m_i)граф  дерево, поэтому выполняется равенство:

n  1 = m = m₁ + m₂ +…+ m_k = (n₁1) +( n₂1) +…+ (n_k1) = (n₁ + n₂ +…+ n_k)  k =

= n  k, т.е. k = 1, следовательно, G  связен, и поэтому любые две несовпадающие вершины u и v соединены в нем простой цепью.

Если предположить, что в G есть две несовпадающие простые (u,v)цепи, то согласно утверждению 5.3 их объединение содержало бы цикл. Следовательно, любые две вершины соединены единственной цепью.

Докажите самостоятельно, что из (4) следует (5), а из (5) следует (1).

Следствие 9.1: в любом дереве порядка n≥2 существует по крайней мере две висячих вершины.

В самом деле, для дерева по лемме о рукопожатиях и все числа deg v_i  0. Следовательно, хотя бы два числа из них равны 1.

Так как в дереве m=n1 рёбер, то чтобы из любого связного графа получить остов (т.е. дерево с теми же вершинами), нужно удалить mn+1 рёбер. Например,

чтобы построить остов связного (6,9)графа G на рис. 9.2, нужно удалить 9  6 + 1 = 4 ребра, сохраняя связность и разрушая циклы графа.

Определение Число V(G) = mn+1 называется циклическим рангом связного графа G.

Следствие 9.2: число ребер произвольного связного графа G, которые нужно удалить для получения остова, не зависит от последовательности их удаления и равно V(G) = mn+1.

Следствие 9.3: связный граф G является деревом тогда и только тогда, когда, когда V(G) = 0.

Следствие 9.4: связный граф G имеет единственный цикл тогда и только тогда, когда, когда V(G) = 1.

Обобщим на случай несвязного графа порядка n с m рёбрами и k компонентами понятие циклического ранга: V(G) = mn+k.

Следствие 9.5: чтобы для произвольного (n,m)графа с k компонентами получить остов, нужно удалить V(G) =m  n + k рёбер.

Чтобы получить остов, нужно в каждой компоненте T_i разрушить все циклы, т. е. оставить m_i  n_i + 1 рёбер (если в компоненте n_i вершин и m_i рёбер).

Суммируя по всем компонентам, получим следствие 9.5.

Определение Число V(G) = mn+k называется циклическим рангом несвязного графа G с k компонентами.

Пусть вершины дерева имеют метки 1, 2, 3, …, n. Такие деревья называются помеченными.

Теорема Кэли. Число помеченных деревьев равно D_n = n^n-2.

При n = 1 и n = 2 формула очевидна.

При n = 3 имеем 3 помеченных дерева (3^3-1=3):

Рис 9.3.

Закодируем каждое помеченное дерево словом, содержащим n-2 символами в алфавите 1, 2, …, n. Полученное слово называется кодом Прюфера для помеченногодерева. Строится этот код так: выбираем в дереве вершинустепени 1 с наименьшей меткой. Сотрем ее вместе с ее ребром и запишем номер, стоящий на другом конце этого ребра. Этот номер будет первым символом кода Прюфера.

Повторяем эту процедуру над оставшимся деревом до тех пор, пока не получится дерево с двумя вершинами. Полученный код является кодом Прюфера помеченного дерева.

Производимое кодирование будет взаимно однозначным: для любого дерева однозначно строится код Прюфера и, наоборот, по коду Прюфера однозначно строится помеченное дерево.

Пример:

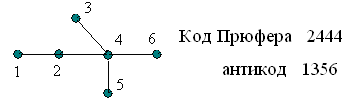
Рис. 9.4.

Общее число слов длины n  2 в алфавите 1, 2, 3, …, n равно n^n-2, столько же будет и помеченных деревьев порядка n.

Правило построения помеченного дерева по коду Прюфера: записываем код и под ним в порядке возрастания те метки, которые не вошли в кодовое слово. Слово, записанное снизу, назовем антикодом (в примере 1356). Вершину, помеченную первой меткой в коде, соединим с вершиной, соответствующей первой метке антикода, после чего вычеркиваем эти метки из кода и антикода. Если вычеркнутая метка кода не встречается в оставшейся части кодового слова, то впишем ее в антикод на соответствующее место. Повторяем эту процедуру до тех пор, пока все метки в коде не будут вычеркнуты. Наконец, соединим две вершины, помеченные метками оставшейся части антикода.

Определение. Дерево называется «корневым», если одна из его вершин выделена (корень дерева).

Следствие (из теоремы Кэли). Число корневых деревьев с n помеченными вершинами равно n^n-1.

Доказательство. В помеченном дереве любую из n вершин можно объявить корнем, поэтому число корневых помеченных деревьев порядка n равно n^n-1.

Пример. Андрей пошел с отцом в тир, с условием: он делает пять выстрелов и за каждое попадание получает право еще на два выстрела. Андрей выстрелил 25 раз. Сколько раз он попал в мишень?

Решение. Стрельбу Андрея можно описать корневым деревом, в котором все вершины, кроме корня (начальное состояние игры  у Андрея 5 патронов), соответствуют выстрелам. Если Андрей попал, то степень соответствующей вершины равна трем, если промазал  единице. Степень корня (верхней вершины) равна пяти. Положение стрельбы после нескольких выстрелов, например, может быть описано корневым деревом, показанным на рис. 9.4:

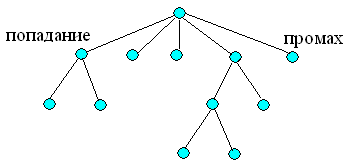
Рис. 9.5.

Дерево стрельбы Андрея имеет 26 вершин и 25 ребер. Пусть n  число попаданий Андрея. Тогда дерево содержит n вершин степени 3, (25  n) вершин степени 1 и одну вершину степени 5. Используя лемму о рукопожатиях, получаем равенство: 3n + (25  n) + 5 =225 или 2n = 20, n =10.

Ответ: Андрей попал 10 раз.

Определение: Корневое дерево называется двоичным, если корень имеет степень 2, а все остальные вершины имеют степень 1 или 3.

Двоичные деревья появляются, например, при вычислении значения выражений (A*B)*(C*D) (рис. 9.6), A*(B*(C*D)) (рис. 9.7):

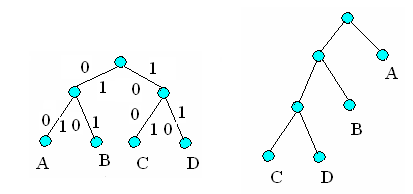
Рис. 9.6 Рис. 9.7

Каждое двоичное дерево можно однозначно закодировать двоичным словом, совершая обход всех вершин графа поиском в глубину, начиная с корня. При этом договоримся писать 0, если ребро проходим первый раз, и 1, если возвращаемся по нему в предыдущую вершину. Дерево на рис. 9.6 закодируется двоичным словом 001011001011.

Дерево на рис.9.7 имеет двоичный код 000101101101.

Каждую висячую вершину двоичного дерева можно закодировать также двоичным словом, двигаясь по единственной цепи от корня к этой вершине, записывая 0 при движении влево и 1 при движении вправо.

Для висячих вершин дерева на рис. 9.7 получим кодовые слова: для А  1, для B  01, для C  000, для D  001.