
8. Частные производные высших порядков
Пусть задана
функция f(x,
y).
Тогда каждая из ее частных
производных(если
они, конечно, существуют) ![]() и
и ![]() ,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная
,
которые называются также частными
производными первого порядка,
снова являются функцией независимых
переменных x,
y и
может, следовательно также иметь частные
производные. Частная производная 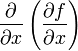 обозначается
через
обозначается
через ![]() или
или ![]() ,
а
,
а  через
через ![]() или
или ![]() .
Таким образом,
.
Таким образом,
 ,
, 
и, аналогично,
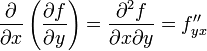 ,
,  .
.
Производные ![]() и
и ![]() называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка:
называются частными
производными второго порядка. Определение:Частной
производной второго порядка от функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка: ![]() ,
, ![]() ,
, ![]() и т. д.
и т. д.
Теорема Шварца — Кристоффеля — важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля.
Очень важной
с практической точки зрения является
проблема о конформном
отображении некой
канонической области (единичного
круга ![]() или
верхней полуплоскости
или
верхней полуплоскости ![]() )
на внутренность произвольного
многоугольника. Важность следующей
теоремы в том, что она дает общий вид
таких отображений.
)
на внутренность произвольного
многоугольника. Важность следующей
теоремы в том, что она дает общий вид
таких отображений.
[править]Теорема
Предположим,
что ![]() —
некоторый
—
некоторый ![]() -угольник,
а функция
-угольник,
а функция ![]() осуществляет
конформное отображение
на
осуществляет
конформное отображение
на ![]() .
Тогда
можно
представить в виде
.
Тогда
можно
представить в виде
 ,
,
где ![]() —
прообразы вершин
на
вещественной оси,
—
прообразы вершин
на
вещественной оси, ![]() —
радианные меры соответствующих внутренних
углов, деленные на
—
радианные меры соответствующих внутренних
углов, деленные на ![]() (то
есть, развернутый угол соответствует
нулевой степени), а
(то
есть, развернутый угол соответствует
нулевой степени), а ![]() и
и ![]() —
так называемыеакцессорные
параметры.
Интеграл в правой части имеет собственное
название — его называют интегралом
Шварца — Кристоффеля I рода.
—
так называемыеакцессорные
параметры.
Интеграл в правой части имеет собственное
название — его называют интегралом
Шварца — Кристоффеля I рода.
В случае, если прообраз одной из вершин многоугольника находится в бесконечности, то формула немного видоизменяется. Если -ая вершина имеет своим прообразом бесконечно удалённую точку, то формула будет иметь вид
 ,
,
то есть множитель, соответствующий этой вершине, будет просто отсутствовать. Такой интеграл будет интегралом Шварца — Кристоффеля II рода.
Трудность использования этих формул состоит в том, что точки , как и акцессорные параметры, в общем случае неизвестны. Для их вычисления обычно на многоугольник накладываются какие-то дополнительные нормировки, либо вычисление производится приближённо (что применяется на практике).
9. Дифференцирование сложной функции
Цепное
правило (правило
дифференцирования сложной функции)
позволяет вычислить производную
композиции двух и более функций на
основе индивидуальных производных.
Если функция f имеет производную в
точке ![]() ,
а функция g имеет производную в точке
,
а функция g имеет производную в точке ![]() ,
то сложная функция h(x) = g(f(x)) также имеет
производную в точке
.
,
то сложная функция h(x) = g(f(x)) также имеет
производную в точке
.
]Одномерный случай
Пусть даны
функции, определённые в окрестностях
на числовой прямой, ![]() где
где ![]() и
и ![]() Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы: ![]() Тогда
их композиция также дифференцируема:
Тогда
их композиция также дифференцируема: ![]() и
её производная имеет вид:
и
её производная имеет вид:
![]()
Замечание
В обозначениях
Лейбница цепное правило для вычисления
производной функции ![]() где
где ![]() принимает
следующий вид:
принимает
следующий вид:
![]()
Инвариантность формы первого дифференциала
Дифференциал
функции ![]() в
точке
в
точке ![]() имеет
вид:
имеет
вид:
![]()
где ![]() —
дифференциал тождественного отображения
—
дифференциал тождественного отображения ![]() :
:
![]()
Пусть
теперь ![]() Тогда
Тогда ![]() ,
и согласно цепному правилу:
,
и согласно цепному правилу:
![]()
Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.
Многомерный случай
Пусть даны
функции ![]() где
и
где
и ![]() Пусть
также эти функции дифференцируемы:
Пусть
также эти функции дифференцируемы: ![]() и
и ![]() Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид
Тогда
их композиция тоже дифференцируема, и
её дифференциал имеет вид
![]()
В частности,
матрица Якоби функции ![]() является
произведением матриц Якоби функций
является
произведением матриц Якоби функций ![]() и
и ![]()
![]()
Следствия
Якобиан композиции двух функций является произведением якобианов индивидуальных функций:

Для частных производных сложной функции справедливо
Дифференцирование неявных функций
Пусть
уравнение ![]() определяет
определяет ![]() как
неявную функцию от х.
как
неявную функцию от х.
а)
продифференцируем по х обе части
уравнения
,
получим уравнение первой степени
относительно ![]() ;
;
б) из полученного уравнения выразим .
Пример:![]() .
.


