
- •1.Плоскость
- •1.4.Основные сведения из теории
- •Решение типовых задач
- •2. Прямая в пространстве
- •2.1. Основные сведения из теории
- •2.2. Решение типовых задач
- •3. Плоскость и прямая в пространстве
- •3.1. Основные сведения из теории
- •3.2. Решение типовых задач
- •Список рекомендуемой литературы
- •Содержание
- •1.2. Решение типовых задач 4
- •2.2. Решение типовых задач 14
- •3.2. Решение типовых задач 21
2. Прямая в пространстве
2.1. Основные сведения из теории
Прямая
![]() в пространстве может быть задана
уравнением одного из следующих видов.
в пространстве может быть задана
уравнением одного из следующих видов.
Общие уравнения прямой:
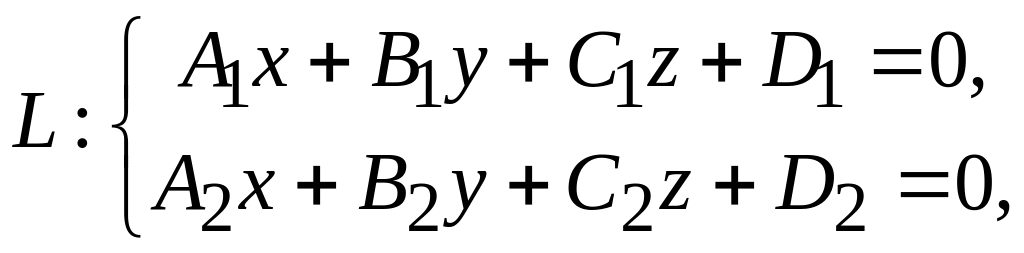 (2.1)
(2.1)
где коэффициенты
![]() не пропорциональны коэффициентам
не пропорциональны коэффициентам
![]() .
Это равносильно заданию прямой как
линии пересечения двух плоскостей.
.
Это равносильно заданию прямой как
линии пересечения двух плоскостей.
Параметрические уравнения прямой:
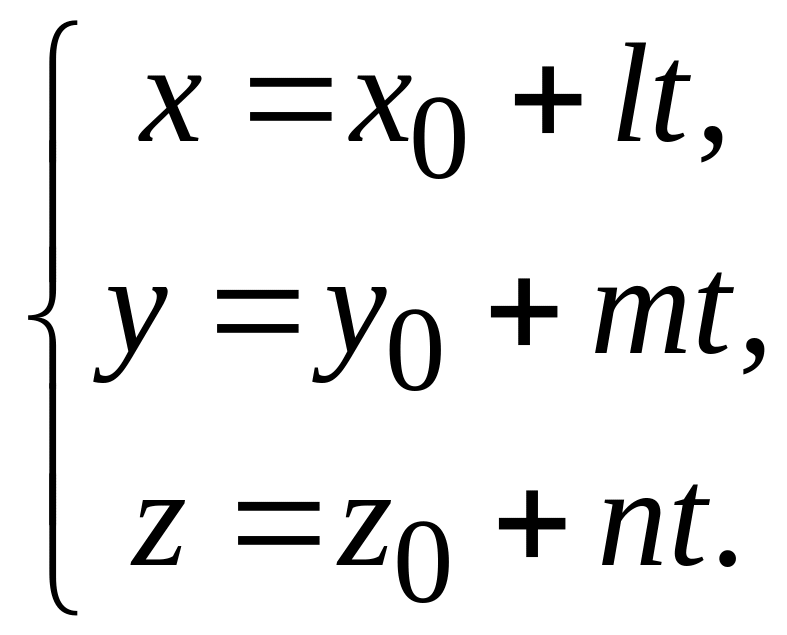 (2.2)
(2.2)
Здесь
![]() – координаты какой-либо точки
– координаты какой-либо точки
![]() принадлежащей прямой
принадлежащей прямой
![]()
![]() – координаты вектора
– координаты вектора
![]() ,
параллельного прямой. Вектор
называется направляющим вектором
прямой. Переменная
,
параллельного прямой. Вектор
называется направляющим вектором
прямой. Переменная
![]() – параметр,
– параметр,
![]()
Канонические уравнения прямой:
![]() (2.3)
(2.3)
4. Уравнения прямой, проходящей через две заданные точки и :
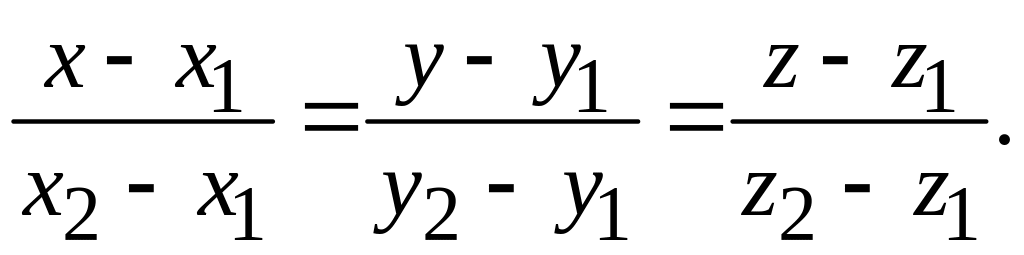 (2.4)
(2.4)
Кроме того, при решении задач будут использоваться следующие формулы, доказательство которых можно найти в теоретическом курсе.
Угол между двумя прямыми
![]()
![]() ;
;
![]()
![]()
равен углу между направляющими векторами
![]() и
и
![]() :
:
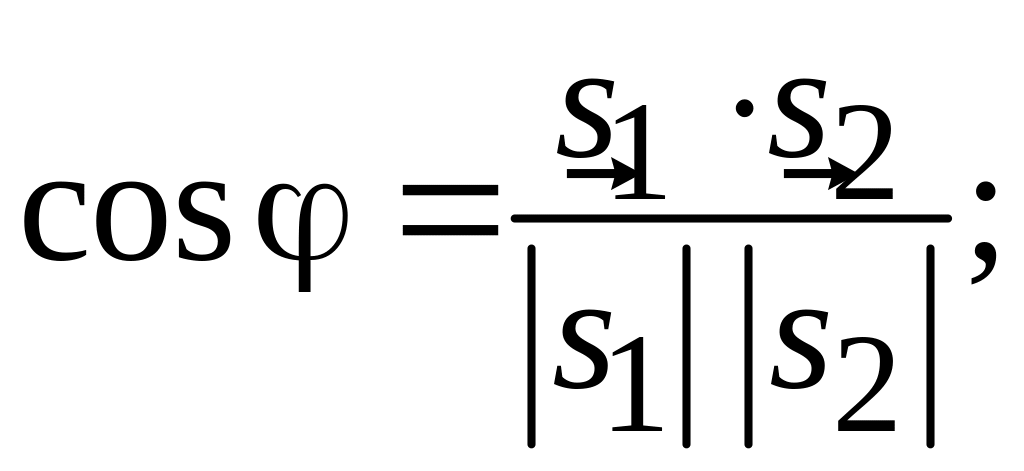
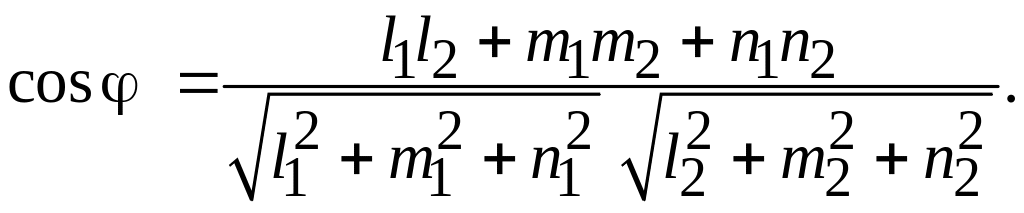 (2.5)
(2.5)
Прямые
![]() и
и
![]() параллельны тогда и только тогда, когда
векторы
параллельны тогда и только тогда, когда
векторы
![]() и
и
![]() коллинеарны (
коллинеарны (![]() ):
):
![]() .
.
Прямые
и
перпендикулярны тогда и только тогда,
когда векторы
и
ортогональны (![]() ):
):
![]()
2.2. Решение типовых задач
Задача 2.1. Найти канонические
уравнения прямой, заданной как линия
пересечения двух плоскостей:

Решение. Прямая
задана общими уравнениями (2.1). Найдем
какую-нибудь точку
на прямой. Выберем, например,
![]() .
Другие координаты получим из системы
уравнений
.
Другие координаты получим из системы
уравнений
 Очевидно, что
Очевидно, что
![]()
![]() .
Следовательно,
.
Следовательно,
![]() .
Затем находим направляющий вектор
прямой. Так как прямая принадлежит
одновременно обеим плоскостям, то вектор
ортогонален нормальным векторам этих
плоскостей, т. е.
.
Затем находим направляющий вектор
прямой. Так как прямая принадлежит
одновременно обеим плоскостям, то вектор
ортогонален нормальным векторам этих
плоскостей, т. е.
![]()
![]() (рис. 2.1). Поэтому за направляющий вектор
можно принять
(рис. 2.1). Поэтому за направляющий вектор
можно принять
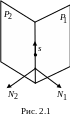
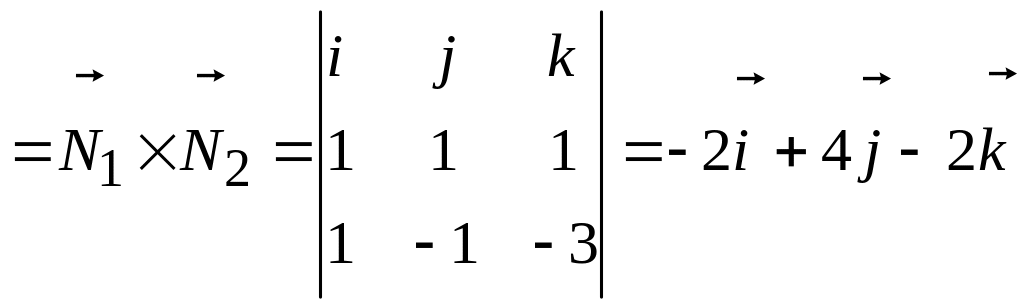 .
.
Подставляя координаты направляющего вектора и точки в уравнения прямой (2.3), получим
![]()
![]() .
.
Ответ: .
Полезная формула. Если прямая задана как линия пересечения двух плоскостей:
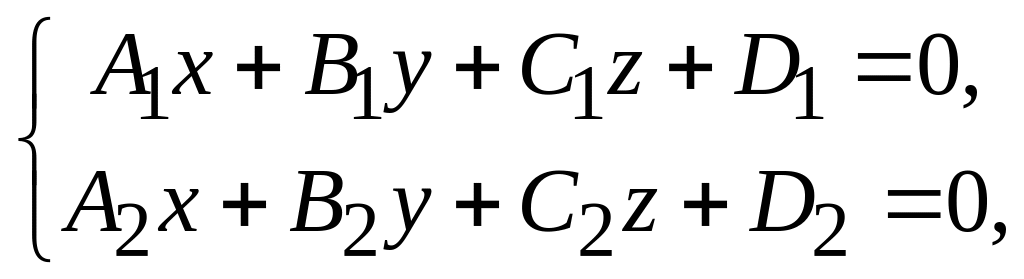
то ее направляющий вектор можно выбрать в виде
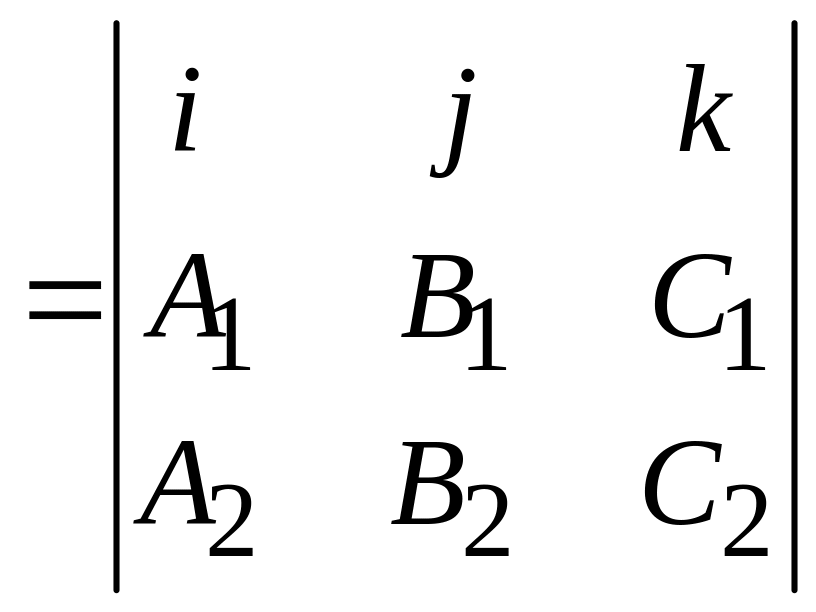 .
(2.6)
.
(2.6)
Задача 2.2. Найти параметрические и
канонические уравнения прямой, проходящей
через точку
![]() и параллельной вектору
и параллельной вектору
![]() .
.
Решение. Известны точка и направляющий вектор прямой.
Согласно формуле (2.2) параметрические уравнения прямой имеют вид
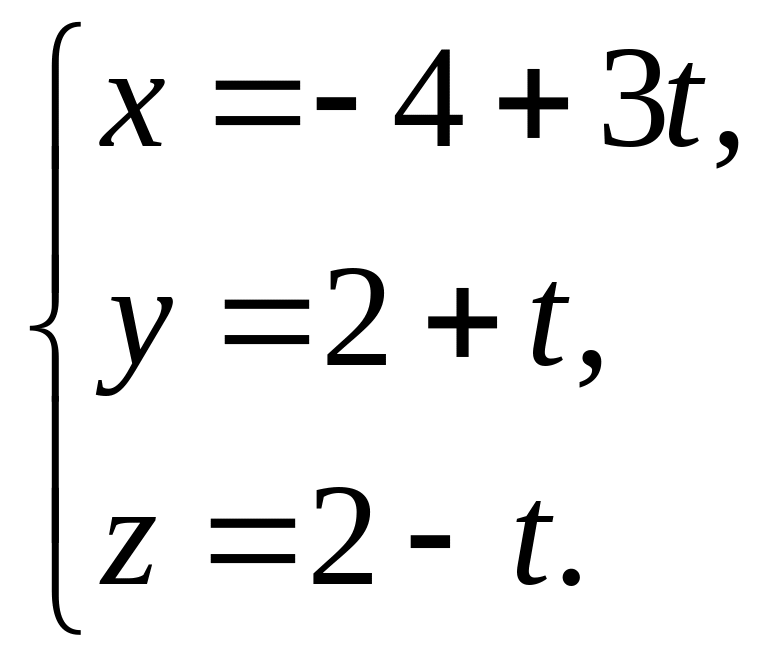
Канонические уравнения получаем, используя формулу (2.3):
![]() .
.
Ответ: .
Задача 2.3. Найти
направляющий
вектор прямой
:
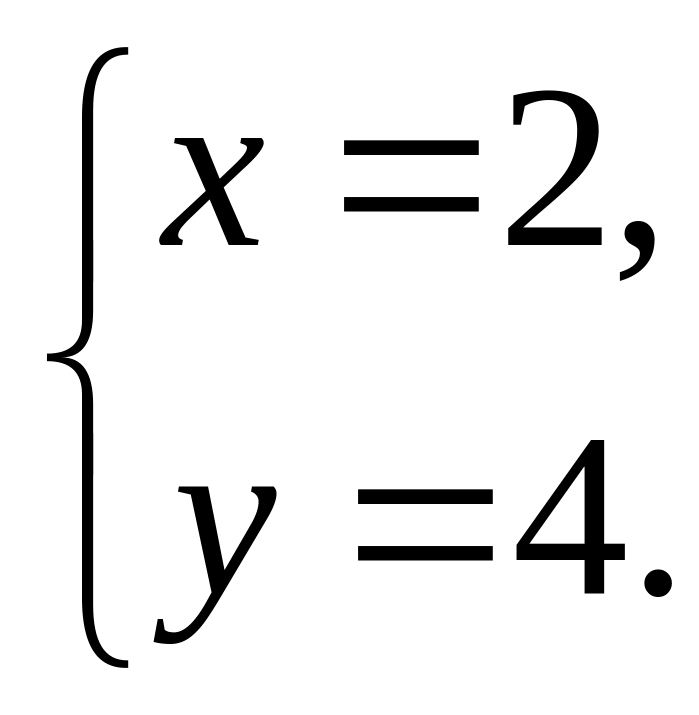
Р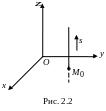 ешение.
Прямая
проходит через точку
(2,
4) на плоскости
ешение.
Прямая
проходит через точку
(2,
4) на плоскости
![]() и параллельна оси
(рис. 2.2). Очевидно, что ее направляющий
вектор можно выбрать в виде
(0,
0, 1).
и параллельна оси
(рис. 2.2). Очевидно, что ее направляющий
вектор можно выбрать в виде
(0,
0, 1).
Ответ: (0, 0, 1).
.
Задача 2.5. Найти косинус острого угла между прямыми
:
![]() ;
:
;
:
![]() .
.
Решение.
Из уравнений прямых вытекает, что
направляющий вектор прямой
равен
![]() ,
направляющий вектор прямой
равен
,
направляющий вектор прямой
равен
![]() .
Для удобства вычислений направляющий
вектор прямой
выберем в виде
.
Для удобства вычислений направляющий
вектор прямой
выберем в виде
![]() .
Он коллинеарен исходному. Используя
формулу (2.5), получаем
.
Он коллинеарен исходному. Используя
формулу (2.5), получаем
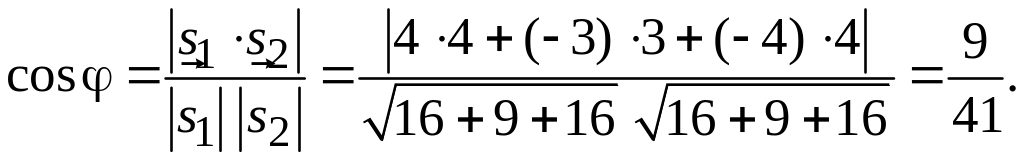
Ответ:
![]()
Задача 2.6. Показать, что прямая
 перпендикулярна прямой
перпендикулярна прямой

Решение. Направляющий вектор первой
прямой, очевидно, равен
![]() ,
направляющий вектор второй прямой
найдем с помощью формулы (2.6):
,
направляющий вектор второй прямой
найдем с помощью формулы (2.6):
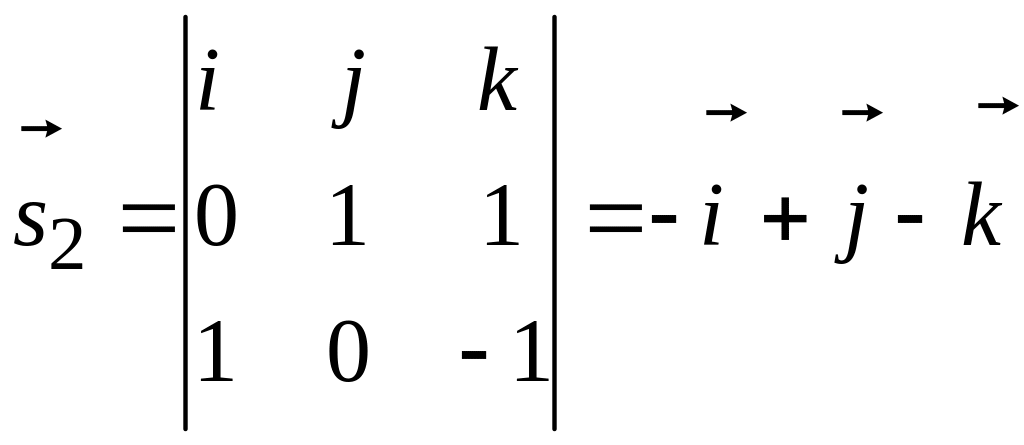 .
.
Вычислим скалярное произведение векторов
и
![]()
![]()
Ответ: прямые перпендикулярны.
Задача 2.7. Проверить, лежат ли три
данные точки
![]() ,
,
![]() и
и
![]() на одной прямой.
на одной прямой.
Решение. Напишем уравнения прямой, проходящей через две заданные точки и , согласно формуле (2.4). Получим
![]()
![]() .
.
П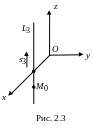 роверим,
удовлетворяют ли координаты точки
этим уравнениям. После подстановки
роверим,
удовлетворяют ли координаты точки
этим уравнениям. После подстановки
![]() получаем:
получаем:
![]() Следовательно, точка
Следовательно, точка
![]() не лежит на прямой.
не лежит на прямой.
Ответ: не лежат.
Задача 2.8. Найти
канонические уравнения прямых
![]() ,
проходящих через точку
,
проходящих через точку
![]() параллельно:
1) оси
параллельно:
1) оси
![]() ;
2) оси
;
2) оси
![]() ;
3) оси
.
;
3) оси
.
Решение.
Найдем уравнения прямой
![]() ,
проходящей через точку
параллельно оси
.
Ее направляющий вектор
,
проходящей через точку
параллельно оси
.
Ее направляющий вектор
![]() можно выбрать в виде
можно выбрать в виде
![]() (рис. 2.3).
(рис. 2.3).
Используя формулу (2.3), получим
:
![]() .
.
Таким же образом находим и .
:
![]() ,
,
![]() ;
;
:
![]() ,
,
![]() .
.
Ответ: : ; : ; : .
Задача 2.9. Найти точки пересечения
прямой
:
![]() с плоскостями координат.
с плоскостями координат.
Решение. Для того чтобы найти точку
пересечения прямой
с плоскостью
,
в канонических уравнениях прямой
следует положить
![]() .
Получим
.
Получим
![]() ,
откуда
,
откуда
![]() ,
,
![]() .
Таким образом, прямая
пересекает плоскость
в точке
.
Таким образом, прямая
пересекает плоскость
в точке
![]() .
Аналогично находим точки пересечения
с плоскостями
и
.
Аналогично находим точки пересечения
с плоскостями
и
![]() .
.
Ответ:
![]() ;
;
![]() ;
;
![]() .
.
З адача
2.10. Известны координаты вершин
тетраэдра:
адача
2.10. Известны координаты вершин
тетраэдра:
![]()
![]()
![]() .
Составить канонические уравнения его
ребер и найти их длины.
.
Составить канонические уравнения его
ребер и найти их длины.
Решение.
Условие такое же, как и в задаче 1.10 (рис.
2.4). Найдем
уравнения ребра
![]() .
Для этого
подставим координаты вершин
.
Для этого
подставим координаты вершин
![]() и
и
![]() в формулу (2.4).
Получим
в формулу (2.4).
Получим
![]() .
Теперь можно определить длину ребра
:
.
Теперь можно определить длину ребра
:
![]() .
.
Уравнения и длины остальных ребер найдите самостоятельно.
Ответ: 1)
:
,
![]() ;
;
2)
![]() :
:
![]() ,
,
![]() ;
;
3)
![]() :
:
![]() ,
,
![]() ;
;
4)
![]() :
:
![]() ,
,
![]() ;
;
5)
![]() :
:
![]() ,
,
![]() ;
;
6)
![]() :
:
![]() ,
,
![]() .
.
Задача 2.11. Найти точку пересечения двух прямых
:
![]() :
:
![]() .
.
Решение. Перепишем уравнения прямых в параметрическом виде
:
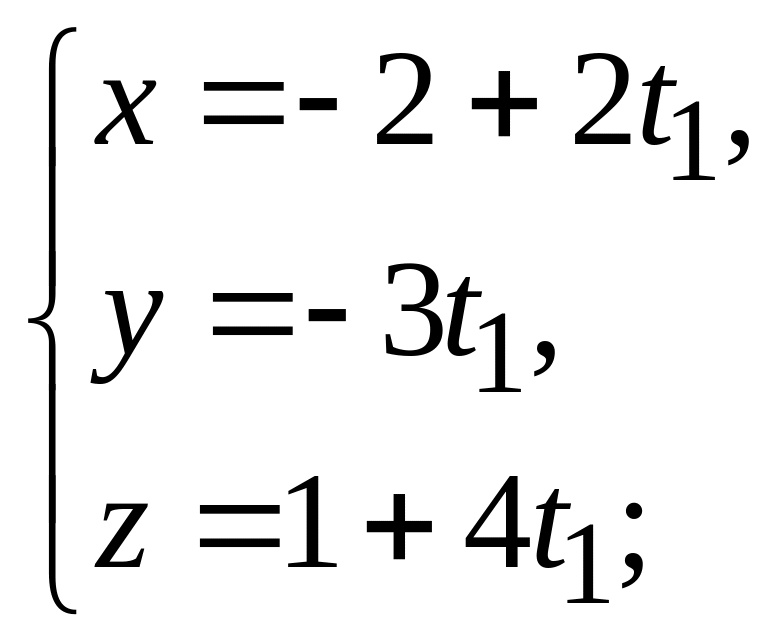 :
:

Для нахождения точки пересечения этих прямых нужно решить систему уравнений:
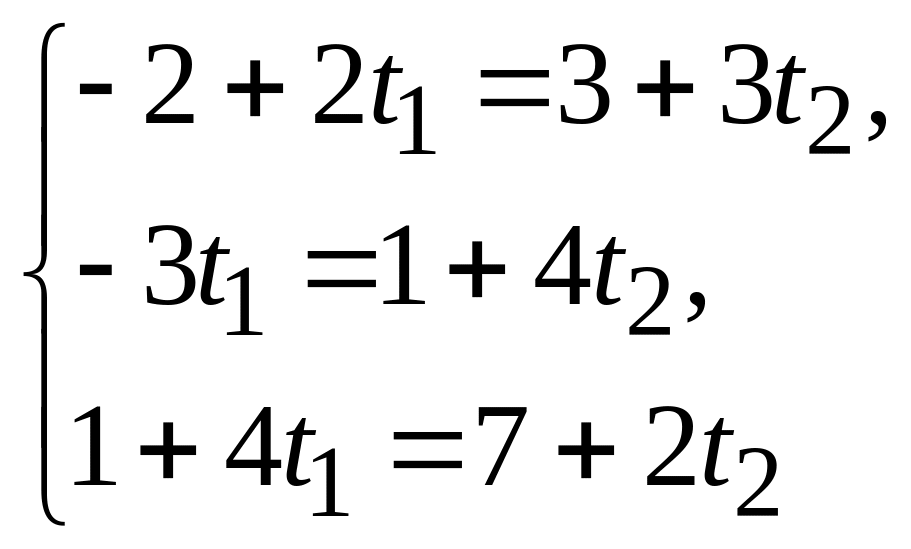

Очевидно, она имеет единственное решение
![]() Подставляя значение параметра
Подставляя значение параметра
![]() в параметрические уравнения прямой
(или
в параметрические уравнения прямой
(или
![]() в уравнения прямой
),
получим
в уравнения прямой
),
получим
![]()
Ответ:
![]() .
.
