
- •1.Плоскость
- •1.4.Основные сведения из теории
- •Решение типовых задач
- •2. Прямая в пространстве
- •2.1. Основные сведения из теории
- •2.2. Решение типовых задач
- •3. Плоскость и прямая в пространстве
- •3.1. Основные сведения из теории
- •3.2. Решение типовых задач
- •Список рекомендуемой литературы
- •Содержание
- •1.2. Решение типовых задач 4
- •2.2. Решение типовых задач 14
- •3.2. Решение типовых задач 21
Задачи на плоскость и прямую в пространстве
Цель настоящих методических указаний заключается в том, чтобы представить набор типовых задач по следующим разделам аналитической геометрии: «Плоскость», «Прямая в пространстве», «Плоскость и прямая». Предложенный набор упражнений ориентирован на освоение ключевых теоретических понятий и утверждений посредством приобретения практических навыков решения стандартных задач по курсу. При этом не требуется применения каких-либо нетрадиционных приемов или теоретических утверждений, выходящих за рамки курса.
1.Плоскость
1.4.Основные сведения из теории
В декартовой системе координат
![]() плоскость
плоскость
![]() может быть задана уравнением одного из
следующих видов.
может быть задана уравнением одного из
следующих видов.
1. Общее уравнение плоскости:
![]()
![]()
![]()
Вектор
![]() перпендикулярен плоскости.
перпендикулярен плоскости.
2. Уравнение
плоскости, проходящей через заданную
точку
![]() перпендикулярно нормальному вектору
,
имеет вид
перпендикулярно нормальному вектору
,
имеет вид
![]() (1.2)
(1.2)
3. Уравнение плоскости в отрезках на осях:
![]() (1.3)
(1.3)
Здесь
![]() величины направленных отрезков,
отсекаемых плоскостью на координатных
осях
величины направленных отрезков,
отсекаемых плоскостью на координатных
осях
![]() соответственно, т. е. плоскость проходит
через три точки:
соответственно, т. е. плоскость проходит
через три точки:
![]() ,
,
![]() ,
,
![]() .
.
Кроме того, понадобятся следующие
формулы, доказательство которых можно
найти в теоретическом курсе.![]()
4. Угол
![]() между двумя плоскостями
между двумя плоскостями
![]()
![]()
и
![]()
![]()
равен углу между нормальными векторами
![]() и
и
![]() :
:
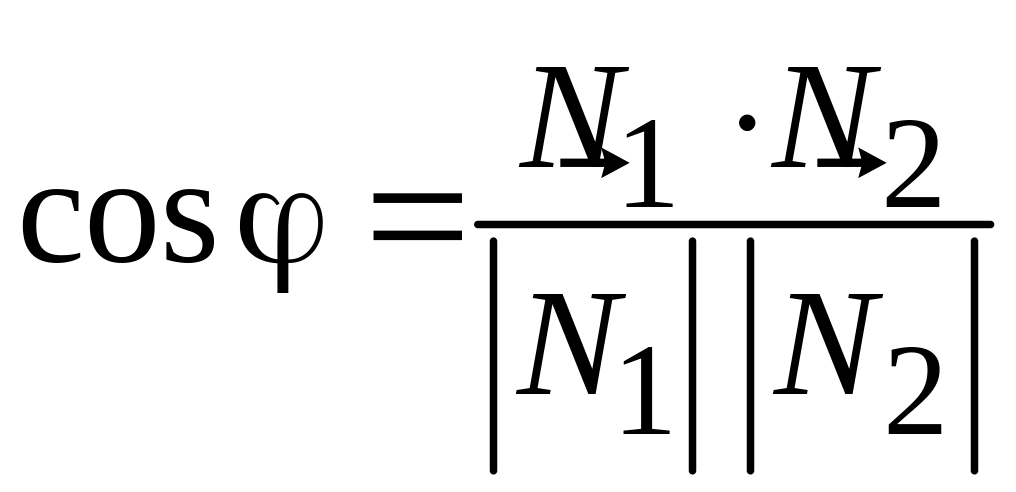 ;
;
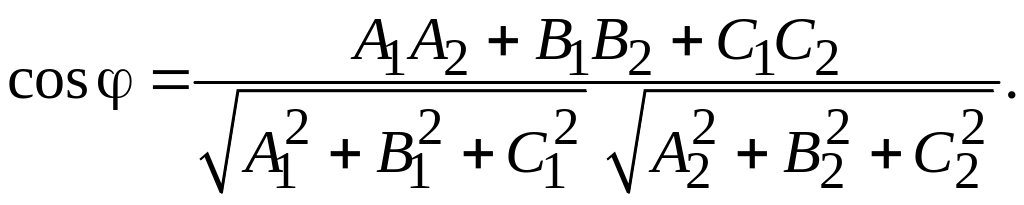 (1.4)
(1.4)
Плоскости
![]() и
и
![]() параллельны тогда и только тогда, когда
векторы
параллельны тогда и только тогда, когда
векторы
![]() и
и
![]() коллинеарны (
коллинеарны (![]() ):
):
![]() .
.
Плоскости
и
перпендикулярны тогда и только тогда,
когда векторы
и
ортогональны (
![]() ):
):
![]()
5. Расстояние
от точки
![]() до плоскости
:
до плоскости
:
![]() равно
равно
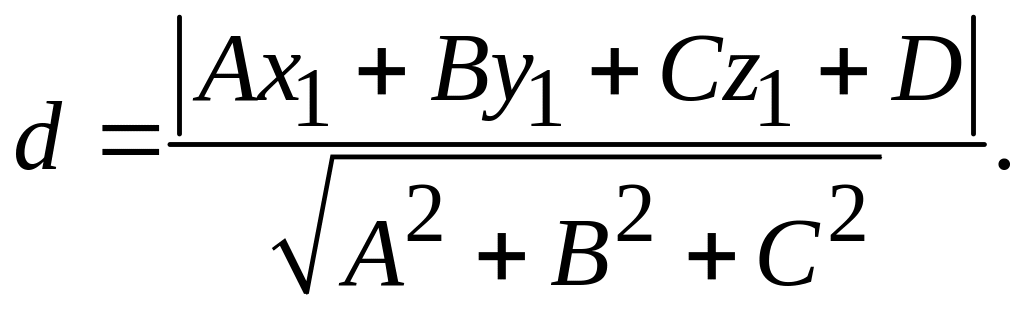 (1.5)
(1.5)
6. Уравнение плоскости, проходящей через линию пересечения двух плоскостей
и
,
следует искать в виде
![]() ,
(1.6)
,
(1.6)
где
![]() и
и
![]() некоторые числа.
некоторые числа.
Множество плоскостей, проходящих через линию пересечения двух заданных плоскостей, называется пучком плоскостей.
Решение типовых задач
Задача 1.1. Составить уравнение плоскости, проходящей через точку
![]() ,
если задан нормальный вектор
,
если задан нормальный вектор
![]() .
.
Р ешение.
Воспользуемся уравнением (1.2):
ешение.
Воспользуемся уравнением (1.2):
![]()
Подставляя координаты вектора
![]() и точки
и точки
![]() ,
получим
,
получим
![]()
![]()
![]()
Ответ:
![]()
Задача 1.2. Составить уравнение
плоскости, проходящей через точку
![]() параллельно векторам
параллельно векторам
![]() и
и
![]() (их называют направляющими векторами
плоскости).
(их называют направляющими векторами
плоскости).
Решение.
П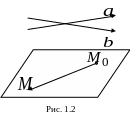 ервый
способ. Пусть
ервый
способ. Пусть
![]() – произвольная точка на плоскости.
Тогда векторы
– произвольная точка на плоскости.
Тогда векторы
![]()
![]() и
и
![]() (рис. 1.2) должны быть компланарны, т. е.
их смешанное произведение должно быть
равно 0:
(рис. 1.2) должны быть компланарны, т. е.
их смешанное произведение должно быть
равно 0:
![]() .
Запишем смешанное произведение через
координаты векторов. Получим
.
Запишем смешанное произведение через
координаты векторов. Получим
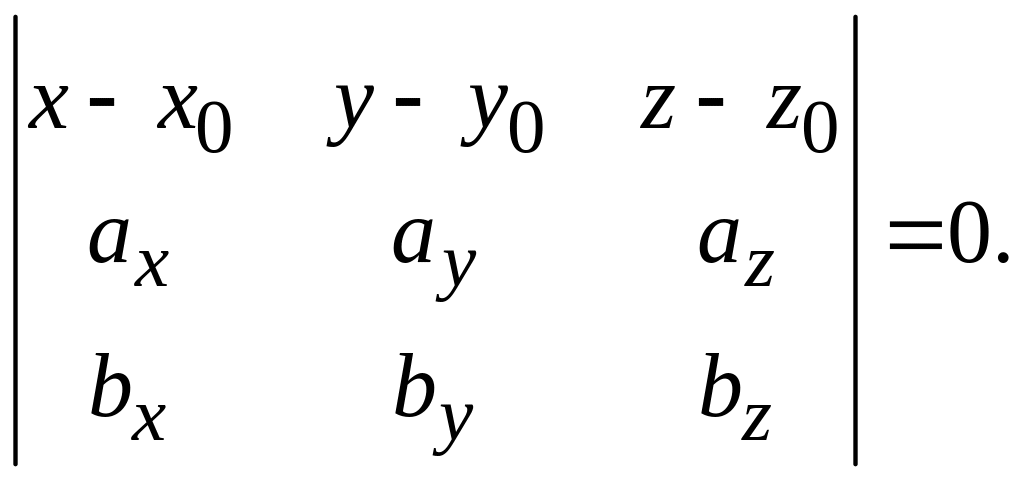
Подставим заданные координаты и вычислим определитель разложением по элементам первой строки:
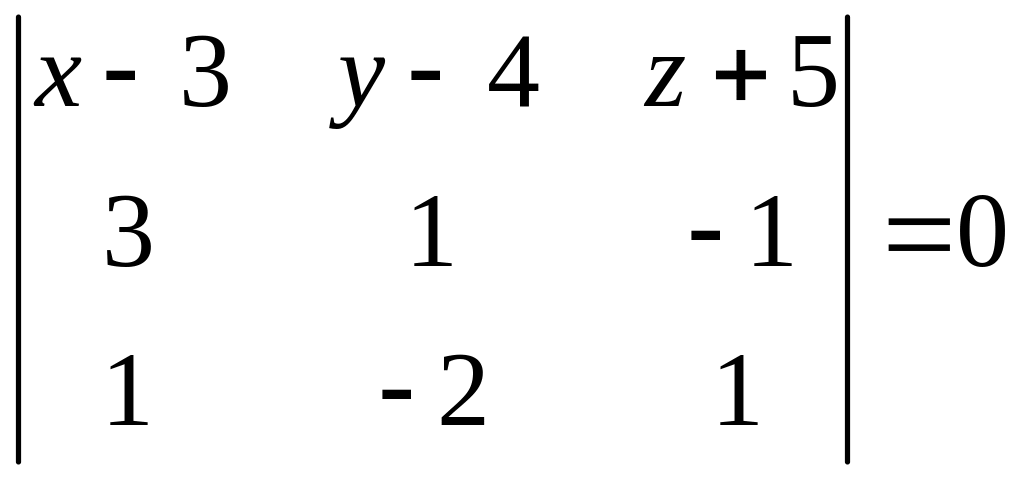 ,
,
или
![]() .
.
Окончательно:
![]()
Второй способ. Найдем сначала вектор
(рис. 1.1). Очевидно, что вектор
нормали
к плоскости должен быть ортогонален
также векторам
и
.
Поэтому его можно выбрать как
векторное произведение
![]()
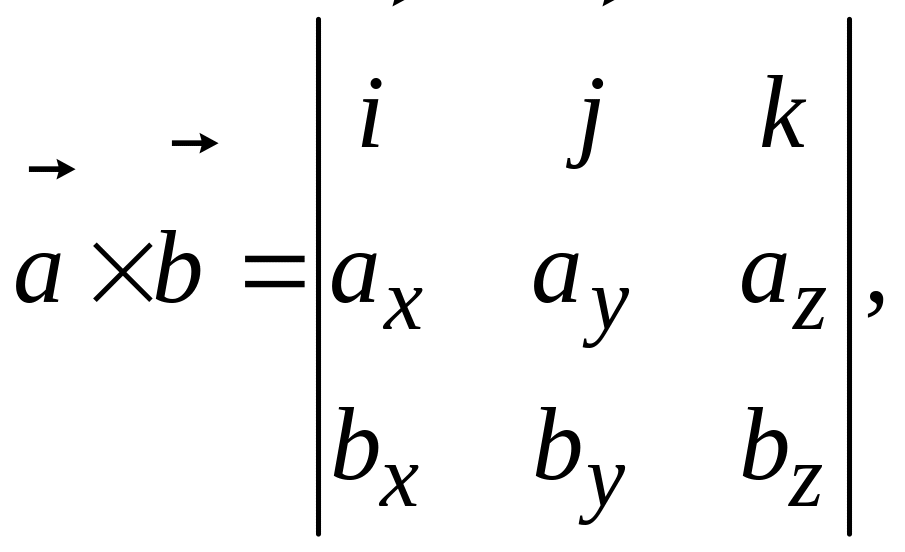
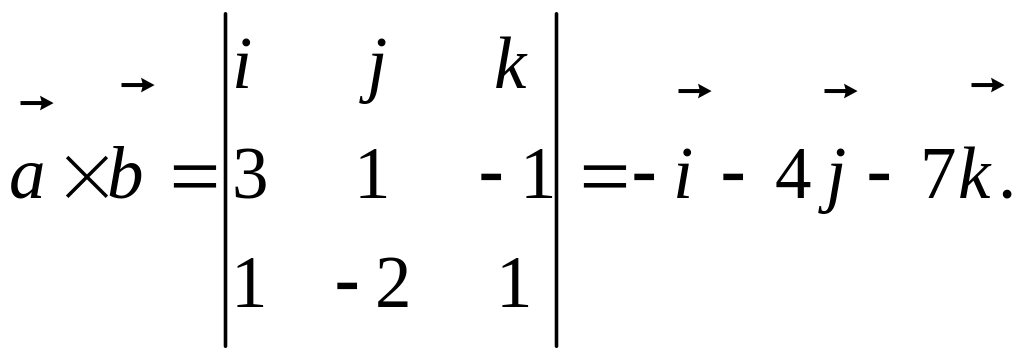
Затем выпишем общее уравнение плоскости,
используя
![]() ,
(см.
формулу (1.2)). Получим
,
(см.
формулу (1.2)). Получим
Ответ:
![]() Полезная
формула. Если
плоскость проходит через точку
,
Полезная
формула. Если
плоскость проходит через точку
,
![]() и
и
![]() – ее направляющие векторы, то уравнение
плоскости имеет вид
– ее направляющие векторы, то уравнение
плоскости имеет вид
(1.7)
Замечание. Первый способ решения
задачи предпочтительнее. Второй способ
отличается лишь тем, что в нем смешанное
произведение трех векторов
![]() ,
,
вычисляется последовательно. А именно:
сначала находим векторное произведение
,
,
вычисляется последовательно. А именно:
сначала находим векторное произведение
![]() и затем результат умножаем скалярно на
вектор
.
В дальнейшем при решении задач будем
придерживаться первого способа.
и затем результат умножаем скалярно на
вектор
.
В дальнейшем при решении задач будем
придерживаться первого способа.
Задача 1.3. Составить уравнение
плоскости, проходящей через точки
![]() и
и
![]() параллельно вектору
параллельно вектору
![]() .
.
Р
![]()
![]() произвольная точка на плоскости.
Тогда векторы
произвольная точка на плоскости.
Тогда векторы
![]() ,
,
![]() и
компланарны (рис. 1.3). Запишем условие
компланарности векторов через их
координаты:
и
компланарны (рис. 1.3). Запишем условие
компланарности векторов через их
координаты:
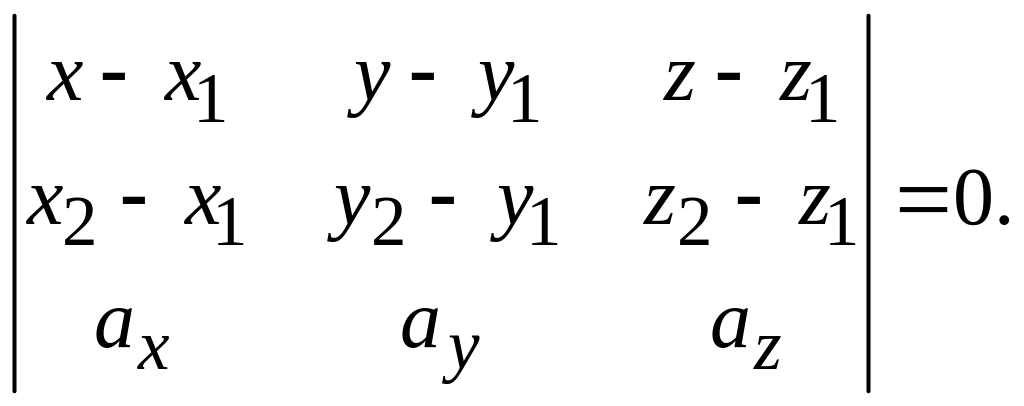
Подставляя заданные координаты, получим
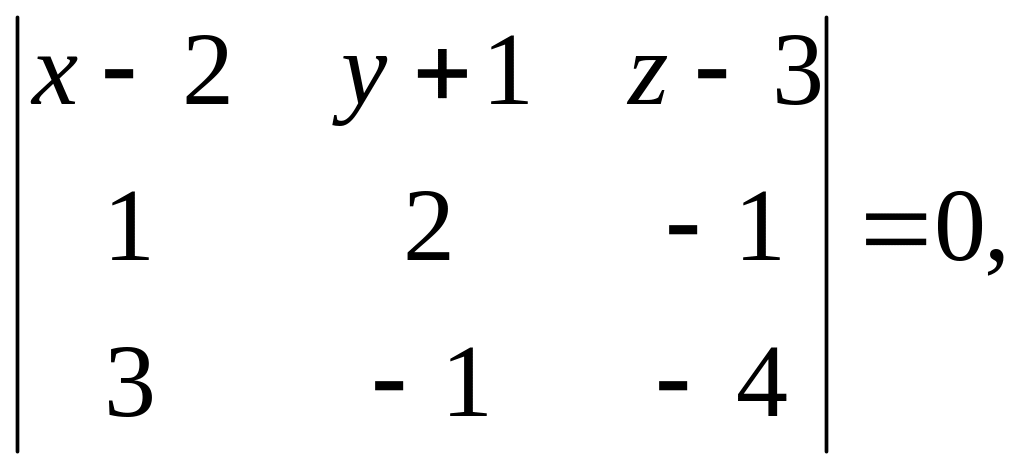
или
![]()
Окончательно:
![]()
Ответ:
Полезная
формула. Если плоскость проходит
через две заданные точки
и
![]() параллельно вектору
,
то ее уравнение имеет вид
параллельно вектору
,
то ее уравнение имеет вид
(1.8)
Задача 1.4. Составить уравнение
плоскости, проходящей через точку
![]() параллельно плоскости
параллельно плоскости
![]()
Решение. В качестве вектора
искомой плоскости можно выбрать
нормальный вектор заданной плоскости,
так как эти плоскости параллельны. Таким
образом, имеем
![]() и
.
Подставляя координаты
и
в уравнение (1.2), получим
и
.
Подставляя координаты
и
в уравнение (1.2), получим
![]()
Окончательно:
![]()
Ответ:
Задача 1.5. Найти величину острого
угла между плоскостями
![]() и
и
![]()
Решение. Угол между плоскостями
равен углу между нормальными векторами
![]() и
и
![]() (см. формулу 1.4)).
(см. формулу 1.4)).
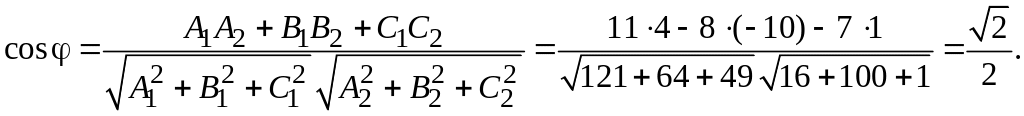
Отсюда
![]()
Ответ:
Задача 1.6. Чему равен угол между
плоскостями
![]() и
и
![]() ?
?
Решение. Найдем скалярное произведение
нормальных векторов
![]() и
и
![]()
![]()
Следовательно, эти плоскости
перпендикулярны:
![]()
Ответ:
Задача 1.7. Составить уравнение
плоскостей, которые проходят через
точку
![]() и отсекают на координатных осях отличные
от нуля отрезки одинаковой длины.
и отсекают на координатных осях отличные
от нуля отрезки одинаковой длины.
Р ешение.
Воспользуемся уравнением плоскости
в отрезках на осях (1.3). Рассмотрим сначала
случай 1:
ешение.
Воспользуемся уравнением плоскости
в отрезках на осях (1.3). Рассмотрим сначала
случай 1:
![]() (рис. 1.4). Тогда
получим
(рис. 1.4). Тогда
получим
![]()
![]()
Подставляя в уравнение координаты точки
,
найдем
![]()
![]()
![]()
Уравнение плоскости:
![]() Затем следует
аналогично рассмотреть случаи 2:
Затем следует
аналогично рассмотреть случаи 2:
![]()
![]() 3:
3:
![]() 4:
4:
![]()
![]() Получим четыре различные плоскости.
Получим четыре различные плоскости.
Ответ:
![]()
![]()
![]()
![]()
Задача 1.8. Построить
плоскости, заданные уравнениями: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]()
![]() ;
4) плоскость
;
4) плоскость
![]() ,
проходящую через точку
,
проходящую через точку
![]() параллельно плоскости
;
5) плоскость
параллельно плоскости
;
5) плоскость
![]() ,
проходящую через точку
,
проходящую через точку
![]() и ось
и ось
![]() .
.
Р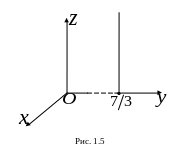
 ешение.
1. Плоскость
параллельна плоскости
ешение.
1. Плоскость
параллельна плоскости
![]() и отсекает на оси
и отсекает на оси
![]() отрезок,
равный
отрезок,
равный
![]() (рис. 1.5).
(рис. 1.5).
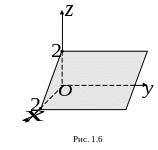
2. Плоскость
![]() параллельна оси
,
пересекает плоскость
параллельна оси
,
пересекает плоскость
![]() по прямой
по прямой
![]() ,
отсекая на осях
,
отсекая на осях
![]() и
отрезки, равные 2 (рис. 1.6).
и
отрезки, равные 2 (рис. 1.6).
3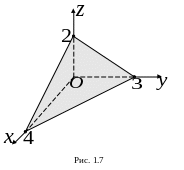
 . Уравнение
плоскости запишем в отрезках на осях
(1.3):
. Уравнение
плоскости запишем в отрезках на осях
(1.3):
![]() .
Плоскость отсекает на осях
,
,
.
Плоскость отсекает на осях
,
,
![]() отрезки, длины которых равны соответственно
4, 3, 2 (рис. 1.7).
отрезки, длины которых равны соответственно
4, 3, 2 (рис. 1.7).
Рис. 1.8
4. Так как плоскость
параллельна плоскости
,
то ее нормальный вектор можно выбрать
в виде
![]() .
Тогда согласно формуле (1.2) уравнение
плоскости
будет
.
Тогда согласно формуле (1.2) уравнение
плоскости
будет
![]() ,
где
,
где
![]() по условию задачи. Таким образом, получаем
по условию задачи. Таким образом, получаем
![]() (рис. 1.8).
(рис. 1.8).
5 .
Плоскость
проходит через ось
.
Поэтому ее нормальный вектор имеет вид
.
Плоскость
проходит через ось
.
Поэтому ее нормальный вектор имеет вид
![]() .
Так как плоскость проходит через начало
координат
.
Так как плоскость проходит через начало
координат
![]() ,
то коэффициент
,
то коэффициент
![]() в уравнении
плоскости (1.1) равен 0. Подставляя
координаты точки
в уравнение
в уравнении
плоскости (1.1) равен 0. Подставляя
координаты точки
в уравнение
![]() ,
получаем
,
получаем
![]() (рис. 1.9).
(рис. 1.9).
Задача 1.9. Составить уравнение
плоскости, проходящей через три заданные
точки
![]()
![]()
![]()
Р ешение.
Пусть
произвольная
точка на плоскости. Тогда векторы
,
,
ешение.
Пусть
произвольная
точка на плоскости. Тогда векторы
,
,
![]() компланарны (рис. 1.10). Запишем условие
компланарности этих векторов через их
координаты:
компланарны (рис. 1.10). Запишем условие
компланарности этих векторов через их
координаты:
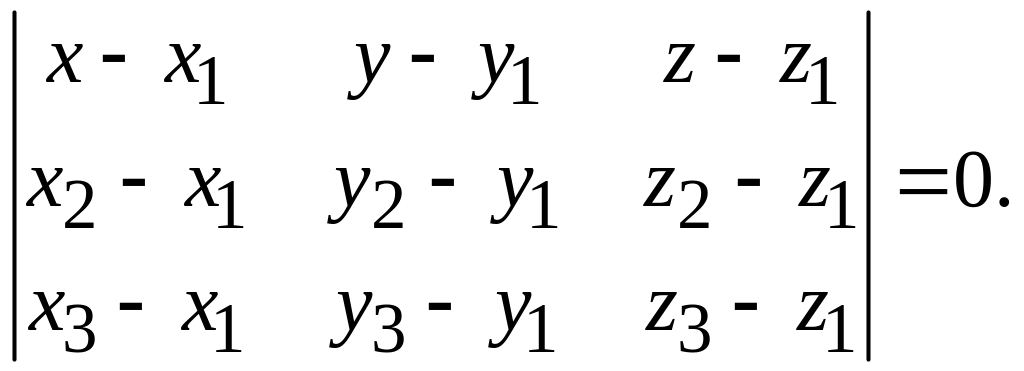 Подставим
значения координат и найдем уравнение
плоскости:
Подставим
значения координат и найдем уравнение
плоскости:
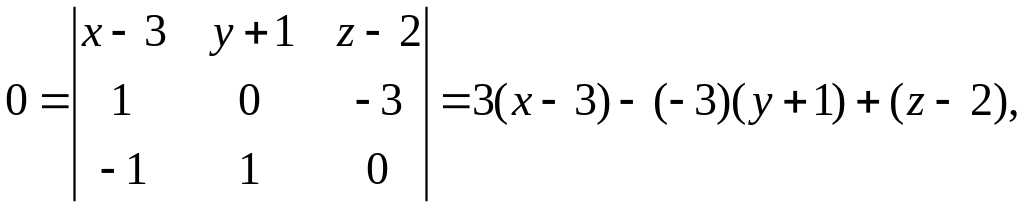
или
![]()
Ответ:
Полезная
формула. Если плоскость проходит
через три заданные точки
![]()
![]()
![]() не лежащие на одной прямой, то ее уравнение
имеет вид
не лежащие на одной прямой, то ее уравнение
имеет вид
(1.9)
Задача 1.10. Даны
координаты вершин тетраэдра:
![]() ,
,
![]() ,
,
![]() ,
,
![]() (рис. 1.11). Составить уравнения его граней.
(рис. 1.11). Составить уравнения его граней.
Р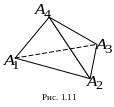 ешение.
Найдем уравнение грани
ешение.
Найдем уравнение грани
![]() .
Для этого подставим в формулу (1.9)
координаты вершин
.
Для этого подставим в формулу (1.9)
координаты вершин
![]() :
:
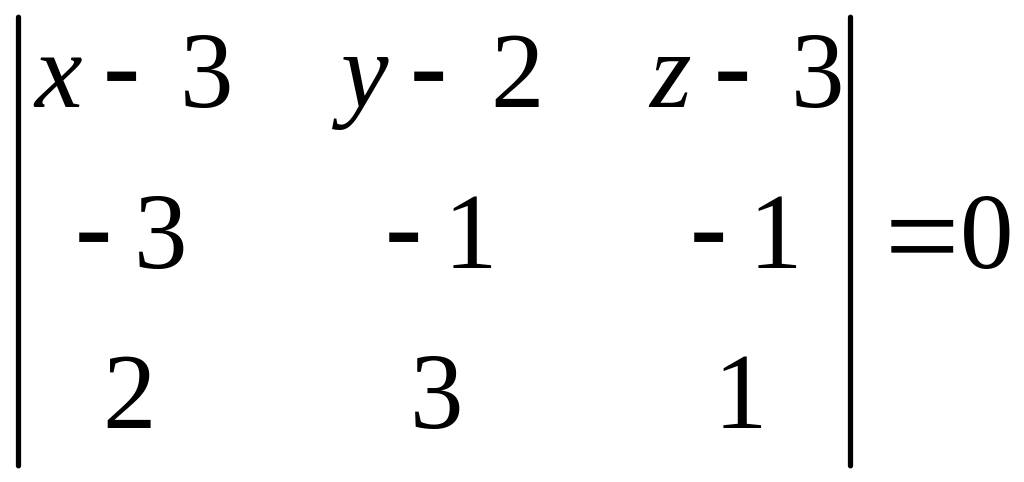 ,
,
или
![]() .
.
Уравнение искомой грани имеет вид
![]()
Уравнения граней
![]() ,
,
![]() ,
,
![]() найдите самостоятельно.
найдите самостоятельно.
Ответ:
![]()
![]()
![]()
![]()
![]() .
.
Задача 1.11. Найти расстояние от точки
![]() до плоскости
до плоскости
![]()
Решение. Используем формулу (1.5):
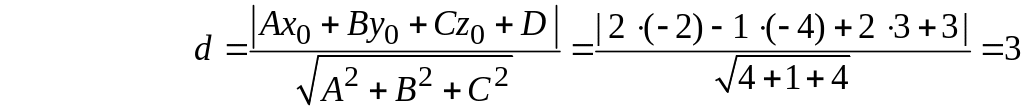 .
.
Ответ:
![]()
Задача 1.12. Найти расстояние между параллельными плоскостями
![]()
![]() .
.
Решение.
Первый способ.
Выберем
произвольно точку
на плоскости
.
Пусть, например,
![]() Тогда
Тогда
![]() Следовательно,
Следовательно,
![]() Найдем расстояние
Найдем расстояние
![]() от
точки
до плоскости
,
по формуле (1.5):
от
точки
до плоскости
,
по формуле (1.5):
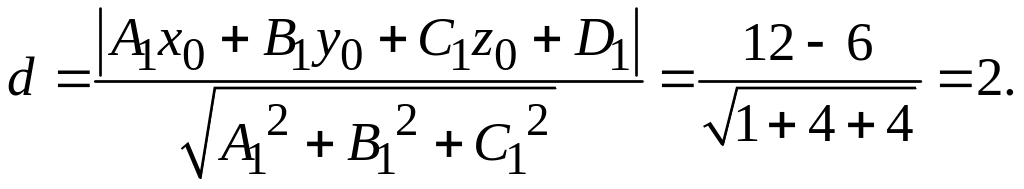
В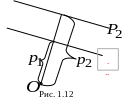 торой
способ. Очевидно, что плоскости
и
лежат по одну сторону относительно
начала координат
торой
способ. Очевидно, что плоскости
и
лежат по одну сторону относительно
начала координат
![]()
Обозначим через
![]() расстояние от начала координат
до плоскости
,
через
расстояние от начала координат
до плоскости
,
через
![]() – до плоскости
(рис. 1.12).
– до плоскости
(рис. 1.12).
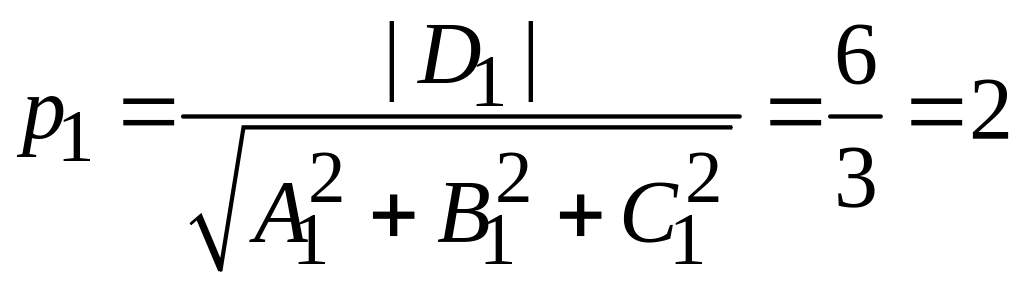
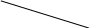 ,
,
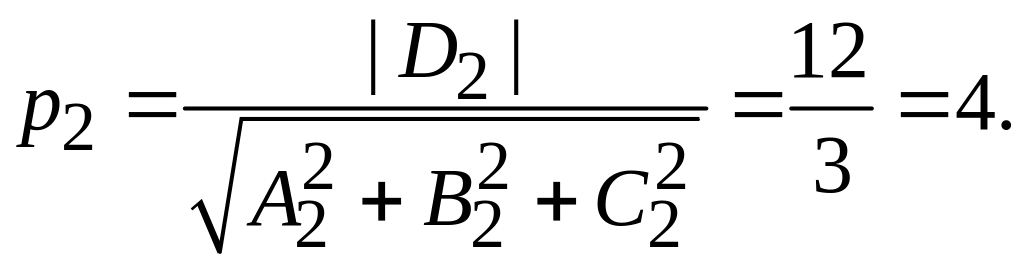
Расстояние между плоскостями равно
![]() .
Отсюда находим
.
Отсюда находим
![]()
Ответ:
![]()
Замечание. Если бы плоскости
находились по разные стороны от начала
координат (рис. 1.13), то расстояние между
ними было бы равно
![]()
