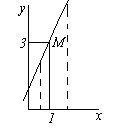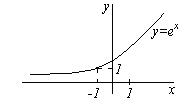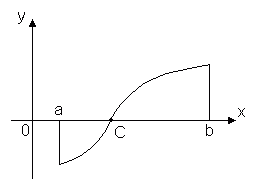Дифференциальное исчисление функций от одной переменной
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ. В результате измерения физических величин (время, площадь, объем, масса, скорость и т.д.) определяются их числовые значения. Математика занимается величинами, отвлекаясь от их конкретного содержания. В дальнейшем, говоря о величинах, мы будем иметь в виду их числовые значения. В различных явлениях некоторые величины изменяются, а другие сохраняют свое числовое значение. Например, при равномерном движении точки время и расстояние меняются, а скорость остается постоянной.
Переменной величиной называется величина, которая принимает различные числовые значения. Величина, числовые значения которой не меняются, называется постоянной. Переменные величины будем обозначать буквами x, y, z,…, постоянные – a, b, c,…
Заметим, что в математике постоянная величина часто рассматривается как частный случай переменной, у которой все числовые значения одинаковы.
Областью изменения переменной величины называется совокупность всех принимаемых ею числовых значений. Область изменения может состоять как из одного или нескольких промежутков, так и из одной точки.
УПОРЯДОЧЕННАЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
Будем говорить, что переменная x есть упорядоченная переменная величина, если известна область ее изменения, и про каждые из двух любых ее значений можно сказать, какое из них предыдущее и какое последующее.
Частным случаем упорядоченной переменной
величины является переменная величина,
значения которой образуют числовую
последовательность x1,x2,…,xn,…
Для таких величин при i < j, i, j
N, значение xi считается
предшествующим, а xj –
последующим независимо от того, какое
из этих значений больше. Таким образом,
числовая последовательность – это
переменная величина, последовательные
значения которой могут быть перенумерованы.
Числовую последовательность будем
обозначать
![]() .
Отдельные числа последовательности
называются ее элементами.
.
Отдельные числа последовательности
называются ее элементами.
Например, числовую последовательность образуют следующие величины:
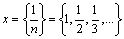 ,
,
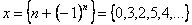 ,
,
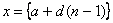 ,
где а, d – постоянные числа.
,
где а, d – постоянные числа.
ФУНКЦИЯ. При изучении различных явлений природы и решении технических задач, а, следовательно, и в математике приходится рассматривать изменение одной величины в зависимости от изменения другой. Так, например, известно, что площадь круга выражается через радиус формулой S = πr2. Если радиус r принимает различные числовые значения, то площадь S также принимает различные числовые значения, т.е. изменение одной переменной влечет изменение другой. Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной y, то y называется функцией переменной х. Символически будем записывать y=f(x). При этом переменная x называется независимой переменной или аргументом.
Запись y=C, где C – постоянная, обозначает функцию, значение которой при любом значении x одно и то же и равно C.
Множество значений x, для которых можно определить значения функции y по правилу f(x), называется областью определения функции.
Заметим, что числовая последовательность также является функцией, область определения которой совпадает с множеством натуральных чисел.
К основным элементарным функциям относятся все функции, изучаемые в школьном курсе математики:
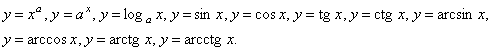
Элементарной функцией называется функция, которая может быть задана основными элементарными функциями и постоянными при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
ПОНЯТИЕ ПРЕДЕЛА ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ.
В дальнейшем курсе математики понятие
предела будет играть фундаментальную
роль, так как с н им
непосредственно связаны основные
понятия математического анализа –
производная, интеграл и др.
им
непосредственно связаны основные
понятия математического анализа –
производная, интеграл и др.
Начнем с понятия предела числовой последовательности.
Число a называется пределом последовательности x = {xn}, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |xn - a| < ε.
Если число a есть предел последовательности
x = {xn}, то говорят, что
xn стремится к a, и пишут
![]() .
.
Выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде
![]()
Это неравенство означает, что все
элементы последовательности с номерами
n>N должны лежать в интервале (a –
ε; a + ε). Этот интервал называется
![]() -окрестностью
точки а.
-окрестностью
точки а.
Следовательно, постоянное число a есть предел числовой последовательности {xn}, если для любой сколь угодно малой окрестности точки a найдется такой элемент последовательности с номером N, что все последующие элементыс номерами n>N будут находиться внутри этой окрестности.
Примеры.
Пусть переменная величина x последовательно принимает значения
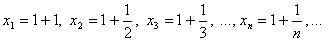 Докажем,
что предел этой числовой последовательности
равен 1. Возьмем произвольное положительное
число ε. Нам нужно найти такое натуральное
число N, что при всех n>N
выполняется неравенство |xn
- 1| < ε. Действительно, т.к.
Докажем,
что предел этой числовой последовательности
равен 1. Возьмем произвольное положительное
число ε. Нам нужно найти такое натуральное
число N, что при всех n>N
выполняется неравенство |xn
- 1| < ε. Действительно, т.к.
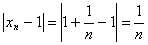 ,
то для выполнения соотношения |xn
- a| < ε достаточно, чтобы
,
то для выполнения соотношения |xn
- a| < ε достаточно, чтобы
 или
или
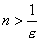 .
Поэтому, взяв в качестве N любое
натуральное число, удовлетворяющее
неравенству
.
Поэтому, взяв в качестве N любое
натуральное число, удовлетворяющее
неравенству
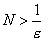 ,
получим что нужно. Так если взять,
например,
,
получим что нужно. Так если взять,
например,
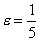 ,
то, положив N=6, для всех n>6 будем
иметь
,
то, положив N=6, для всех n>6 будем
иметь
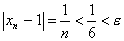 .
.Используя определение предела числовой последовательности, доказать что
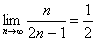 .
.
Возьмем произвольное ε > 0. Рассмотрим
![]() .
.
Тогда
![]() ,
если
,
если
![]() или
или
![]() ,
т.е.
,
т.е.
![]() .
Поэтому выберем любое натуральное
число, удовлетворяющее неравенству
.
Поэтому выберем любое натуральное
число, удовлетворяющее неравенству
![]() .
.
Сделаем несколько замечаний.
Замечание 1. Очевидно, что если все элементы числовой последовательности принимают одно и то же постоянное значение xn = c, то предел этой последовательности будет равен самой постоянной. Действительно, при любом ε всегда выполняется неравенство |xn - c| = |c - c| = 0 < ε.
Замечание 2. Из определения предела
следует, что последовательность не
может иметь двух пределов. Действительно,
предположим, что xn → a
и одновременно xn → b.
Возьмем любое
![]() и
отметим окрестности точек a и b
радиуса ε. Тогда по определению предела,
все элементы последовательности, начиная
с некоторого, должны находиться как в
окрестности точки а, так и в окрестности
точки b, что невозможно.
и
отметим окрестности точек a и b
радиуса ε. Тогда по определению предела,
все элементы последовательности, начиная
с некоторого, должны находиться как в
окрестности точки а, так и в окрестности
точки b, что невозможно.
Замечание 3. Не следует думать, что
каждая числовая последовательность
имеет предел. Пусть, например, переменная
величина принимает значения
![]() .
Несложно заметить, что эта последовательность
не стремится ни к какому пределу.
.
Несложно заметить, что эта последовательность
не стремится ни к какому пределу.
ПРЕДЕЛ ФУНКЦИИ. Пусть функция y=f(x) определена в некоторой окрестности точки a. Предположим, что независимая переменная x неограниченно приближается к числу a. Это означает, что мы можем придавать х значения сколь угодно близкие к a, но не равные a. Будем обозначать это так x → a. Для таких x найдем соответствующие значения функции. Может случиться, что значения f(x) также неограниченно приближаются к некоторому числу b.Тогда говорят, что число b есть предел функции f(x) при x → a. Введем строгое определение предела функции.
Функция y=f(x) стремится к пределу b
при x → a, если для каждого положительного
числа ε, как бы мало оно не было, можно
указать такое положительное число δ,
что при всех x ≠ a из области определения
функции, удовлетворяющих неравенству
|x - a| < δ, имеет место неравенство
|f(x) - b| < ε. Если b есть предел
функции f(x) при x → a, то пишут
Проиллюстрируем это определение на графике функции. Т.к. из неравенства |x - a| < δ должно следовать неравенство |f(x) - b| < ε, т.е. при x (a - δ, a + δ) соответствующие значения функции f(x) (b - ε, b + ε), то,взяв произвольное ε > 0,мы можем подобрать такое число δ, что для всех точек x, лежащих в δ – окрестности точки a, соответствующие точки графика функции должны лежать внутри полосы шириной 2ε, ограниченной прямыми y = b – ε и y = b + ε.
Несложно заметить, что предел функции
должен обладать теми же свойствами,
что и предел числовой последовательности,
а именно
Примеры.
|
Рис.к 2 |
ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ В БЕСКОНЕЧНО УДАЛЕННОЙ ТОЧКЕ. До сих пор мы рассматривали пределы для случая, когда переменная величина x стремилась к определенному постоянному числу.
Будем говорить, что переменная x стремится к бесконечности, если для каждого заранее заданного положительного числа M (оно может быть сколь угодно большим) можно указать такое значение х=х0, начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x|>M.
Например, пусть переменная х принимает значения x1= –1, x2=2, x3= –3, …, xn=(–1)nn, … Ясно, что это бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M.
Переменная величина x → +∞, если при произвольном M > 0 все последующие значения переменной, начиная с некоторого, удовлетворяют неравенству x > M.
Аналогично, x → – ∞, если при любом M > 0 x < -M.
Будем говорить, что функция f(x)
стремится к пределу b при x → ∞,
если для произвольного малого
положительного числа ε можно указать
такое положительное число M, что для
всех значений x, удовлетворяющих
неравенству |x|>M, выполняется
неравенство |f(x)-b| < ε. Обозначают
![]() .
.
П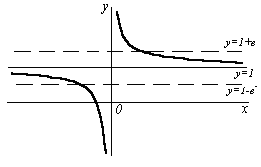 римеры.
римеры.
Используя определение, доказать, что
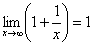 .
.
Нужно доказать, что при произвольном ε
будет выполняться неравенство
![]() ,
как только |x|>M, причем число М
должно определяться выбором ε. Записанное
неравенство эквивалентно следующему
,
как только |x|>M, причем число М
должно определяться выбором ε. Записанное
неравенство эквивалентно следующему
![]()
![]() ,
которое будет выполняться, если |x|>1/ε=M.
Это и значит, что
(см.
рис.).
,
которое будет выполняться, если |x|>1/ε=M.
Это и значит, что
(см.
рис.).
Несложно заметить, что
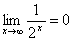 .
.
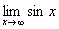 не
существует.
не
существует.
БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ. Ранее мы рассмотрели случаи, когда функция f(x) стремилась к некоторому конечному пределу b при x → a или x → ∞.
Рассмотрим теперь случай, когда функция y=f(x) стремится к бесконечности при некотором способе изменения аргумента.
Функция f(x) стремится к бесконечности при x → a, т.е. является бесконечно большой величиной, если для любого числа М, как бы велико оно ни было, можно найти такое δ > 0, что для всех значений х≠a, удовлетворяющих условию |x-a| < δ, имеет место неравенство |f(x)| > M.
Если f(x) стремится к бесконечности
при x→a, то пишут
![]() или
f(x)→∞ при x→a.
или
f(x)→∞ при x→a.
Сформулируйте аналогичное определение для случая, когда x→∞.
Если f(x) стремится к бесконечности
при x→a и при этом принимает только
положительные или только отрицательные
значения, соответственно пишут
![]() или
или
![]() .
.
Примеры.
 .
.
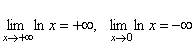 (см.
рис.).
(см.
рис.).
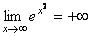 .
.
Функция
 при
x→0 не стремится ни к какому пределу
(см. рис.).
при
x→0 не стремится ни к какому пределу
(см. рис.).
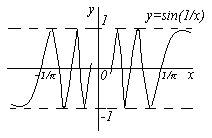
ОГРАНИЧЕННЫЕ ФУНКЦИИ. Пусть задана функция y=f(x), определенная на некотором множестве D значений аргумента.
Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D.
Примеры.
Функция y=sin x, определенная при -∞<x<+∞, является ограниченной, так как при всех значениях x |sin x|≤1 = M.
Функция y=x2+2 ограничена, например, на отрезке [0, 3], так как при всех x из этого отрезка |f(x)| ≤f(3) = 11.
Рассмотрим функцию y=ln x при x (0; 1). Эта функция неограниченна на указанном отрезке, так как при x→0 ln x→-∞.
Функция y=f(x) называется ограниченной при x → a, если существует окрестность с центром в точке а, в которой функция ограничена.
Функция y=f(x) называется ограниченной при x→∞, если найдется такое число N>0, что при всех значениях х, удовлетворяющих неравенству |x|>N, функция f(x) ограничена.
Установим связь между ограниченной функцией и функцией, имеющей предел.
Теорема 1. Если
![]() и
b – конечное число, то функция f(x)
ограничена при x→a.
и
b – конечное число, то функция f(x)
ограничена при x→a.
Доказательство. Т.к. , то при любом ε>0 найдется такое число δ>0, что при вех значениях х, удовлетворяющих неравенству |x-a|<δ, выполняется неравенство |f(x) –b|<ε. Воспользовавшись свойством модуля |f(x) – b|≥|f(x)| - |b|, последнее неравенство запишем в виде |f(x)|<|b|+ ε. Таким образом, если положить M=|b|+ ε, то при x→a |f(x)|<M.
Замечание. Из определения ограниченной функции следует, что если , то она является неограниченной. Однако обратное неверно: неограниченная функция может не быть бесконечно большой. Приведите пример.
Теорема 2. Если
![]() ,
то функция y=1/f(x) ограничена при x→a.
,
то функция y=1/f(x) ограничена при x→a.
Доказательство. Из условия теоремы
следует, что при произвольном ε>0 в
некоторой окрестности точки a имеем
|f(x) – b|<ε. Т.к. |f(x) – b|=|b – f(x)| ≥|b|
- |f(x)|, то |b| - |f(x)|< ε. Следовательно,
|f(x)|>|b| - ε >0. Поэтому и
![]() .
.
БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ
СВОЙСТВА. Функция y=f(x) называется
бесконечно малой при x→a или при
x→∞, если
![]() или
или
![]() ,
т.е. бесконечно малая ф
,
т.е. бесконечно малая ф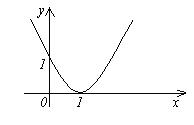 ункция
– это функция, предел которой в данной
точке равен нулю.
ункция
– это функция, предел которой в данной
точке равен нулю.
Примеры.
Функция f(x)=(x-1)2 является бесконечно малой при x→1, так как
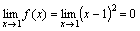 (см.
рис.).
(см.
рис.).
Функция f(x) = tgx – бесконечно малая при x→0.
f(x) = ln (1+x)– бесконечно малая при x→0.
f(x) = 1/x– бесконечно малая при x→∞.
Установим следующее важное соотношение:
Теорема. Если функция y=f(x) представима при x→a в виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x), то .
Обратно, если , то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.
Доказательство.
Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .
Если , то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.
Рассмотрим основные свойства бесконечно малых функций.
Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
Доказательство. Приведем доказательство
для двух слагаемых. Пусть f(x)=α(x)+β(x),
где
![]() и
и
![]() .
Нам нужно доказать, что при произвольном
как угодно малом ε>0 найдется δ>0,
такое, что для x, удовлетворяющих
неравенству |x – a|<δ, выполняется
|f(x)|< ε.
.
Нам нужно доказать, что при произвольном
как угодно малом ε>0 найдется δ>0,
такое, что для x, удовлетворяющих
неравенству |x – a|<δ, выполняется
|f(x)|< ε.
Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.
Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,
т.е. |f(x)|<ε, что и требовалось доказать.
Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.
Из доказанной теоремы вытекают:
Следствие 1. Если
и
,
то
![]() .
.
Следствие 2. Если
и
c=const, то
![]() .
.
Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
Доказательство. Пусть
![]() .
Тогда 1/f(x) есть ограниченная функция.
Поэтому дробь
.
Тогда 1/f(x) есть ограниченная функция.
Поэтому дробь
![]() есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
есть
произведение бесконечно малой функции
на функцию ограниченную, т.е. функция
бесконечно малая.
СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ
ТЕОРЕМА 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Доказательство. Возьмем произвольное
число ε>0 и покажем, что при некотором
δ>0 (зависящим от ε) при всех x,
для которых |x – a|<δ, выполняется
неравенство
![]() ,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) – бесконечно большая
функция при x→a, то найдется δ>0
такое, что как только |x – a|<δ, так
|f(x)|>1/ ε. Но тогда для тех же x
.
,
а это и будет означать, что 1/f(x) –
бесконечно малая функция. Действительно,
так как f(x) – бесконечно большая
функция при x→a, то найдется δ>0
такое, что как только |x – a|<δ, так
|f(x)|>1/ ε. Но тогда для тех же x
.
Примеры. 1. Ясно, что при x→+∞ функция
y=x2+1 является бесконечно
большой. Но тогда согласно сформулированной
выше теореме функция
![]() –
бесконечно малая при x→+∞, т.е.
–
бесконечно малая при x→+∞, т.е.
![]() .
2.
.
2.
![]() .
Можно доказать и обратную ТЕОРЕМУ.
.
Можно доказать и обратную ТЕОРЕМУ.
ТЕОРЕМА 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Доказательство теоремы проведите самостоятельно.
Примеры.
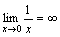 .
.
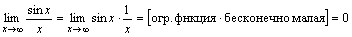 .
.
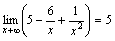 ,
так как функции
,
так как функции
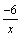 и
и
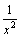 -
бесконечно малые при x→+∞, то
-
бесконечно малые при x→+∞, то
 ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
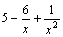 является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
![]() .
.
ТЕОРЕМЫ О ПРЕДЕЛАХ.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
![]() .
.
Доказательство. Проведем доказательство
для двух слагаемых, так как для любого
числа слагаемых оно проводится так же.
Пусть
![]() .Тогда
f(x)=b+α(x) и g(x)=c+β(x), где α и β
– бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
.Тогда
f(x)=b+α(x) и g(x)=c+β(x), где α и β
– бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то
![]() .
.
Пример.
![]() .
.
Теорема 2. Предел произведения двух,
трех и вообще конечного числа функций
равен произведению пределов этих
функций:
![]() .
.
Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть величина
постоянная. Функция bβ + c α + αβ на
основании свойств бесконечно малых
функций есть величина бесконечно малая.
Поэтому
![]() .
.
Следствие 1. Постоянный множитель
можно выносить за знак предела:
![]() .
.
Следствие 2. Предел степени равен
степени предела:
![]() .
.
Пример.
![]() .
.
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
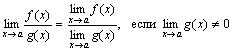 .
.
Доказательство. Пусть
![]() .
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α, β – бесконечно малые. Рассмотрим
частное
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x),
где α, β – бесконечно малые. Рассмотрим
частное
![]() .
.
Дробь
![]() является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
является
бесконечно малой функцией, так как
числитель есть бесконечно малая функция,
а знаменатель имеет предел c2≠0.
Примеры.
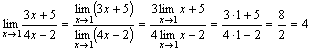 .
.
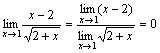 .
.
Рассмотрим
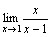 .
При x→1 числитель дроби стремится
к 1, а знаменатель стремится к 0. Но так
как
.
При x→1 числитель дроби стремится
к 1, а знаменатель стремится к 0. Но так
как
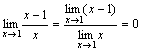 ,
т.е.
,
т.е.
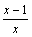 есть
бесконечно малая функция при x→1,
то
есть
бесконечно малая функция при x→1,
то
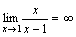
 .
.
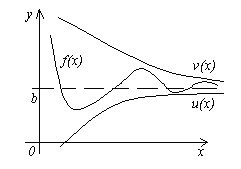
Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x) стремится к тому же пределу, т.е. если
![]() ,
то
,
то
![]() .
.
Смысл этой теоремы понятен из рисунка.
Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.
Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.
Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.
Т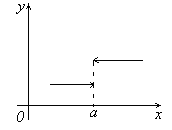 еорема
6. Если две функции f(x) и g(x) при
всех значениях аргумента x удовлетворяют
неравенству f(x)≥ g(x) и имеют пределы
еорема
6. Если две функции f(x) и g(x) при
всех значениях аргумента x удовлетворяют
неравенству f(x)≥ g(x) и имеют пределы
![]() ,
то имеет место неравенство b≥c.
,
то имеет место неравенство b≥c.
Доказательство. По условию теоремы
f(x)-g(x) ≥0, следовательно, по теореме
5
![]() ,
или
,
или
![]() .
.
ОДНОСТОРОННИЕ ПРЕДЕЛЫ. До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.
Если f(x) стремится к пределу b
при x стремящемся к некоторому числу
a так, что xпринимает только
значения, меньшие a, то пишут
![]() и
называют b пределом функции f(x) в точке
a слева.
и
называют b пределом функции f(x) в точке
a слева.
Таким образом, число b называется
пределом функции y=f(x) при x→a слева,
если каково бы ни было положительное
число ε, найдется такое число δ (меньшее
a), что для всех
![]() выполняется
неравенство
выполняется
неравенство
![]() .
.
Аналогично, если x→a и принимает
значения большие a, то пишут
![]() и
называют b пределом функции в точке
а справа. Т.е. число b называется
пределом функции y=f(x) при x→a справа,
если каково бы ни было положительное
число ε, найдется такое число δ (большее
а), что для всех
и
называют b пределом функции в точке
а справа. Т.е. число b называется
пределом функции y=f(x) при x→a справа,
если каково бы ни было положительное
число ε, найдется такое число δ (большее
а), что для всех
![]() выполняется
неравенство
.
выполняется
неравенство
.
Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.
Примеры.
Рассмотрим функцию y=f(x), определенную на отрезке [0,1] следующим образом
![]()
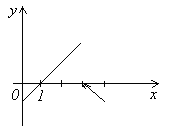
Найдем пределы функции f(x) при x→3.
Очевидно,
![]() ,
а
,
а
![]() .
.
2.
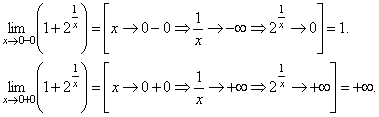
3.
![]() .
.
4.
 .
.
ТИПЫ НЕОПРЕДЕЛЕННОСТЕЙ И СПОСОБЫ ИХ
РАСКРЫТИЯ. Часто при вычислении
пределов какой-либо функции, непосредственное
применение теорем о пределах не приводит
к желаемой цели. Так, например, нельзя
применять теорему о пределе дроби, если
ее знаменатель стремится к нулю. Поэтому
часто прежде, чем применять эти теоремы,
необходимо тождественно преобразовать
функцию, предел которой мы ищем. Условные
выражения
![]() характеризуют
типы неопределенностей и применяются
для обозначения переменных величин,
при вычислении предела которых нельзя
сразу применять общие свойства пределов.
характеризуют
типы неопределенностей и применяются
для обозначения переменных величин,
при вычислении предела которых нельзя
сразу применять общие свойства пределов.
Рассмотрим некоторые ПРИЕМЫ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ.
I. Неопределенность
![]() .
.
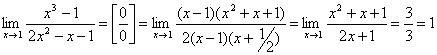 .
.
 .
.
При разложении числителя на множители воспользовались правилом деления многочлена на многочлен «углом». Так как число x=1 является корнем многочлена x3 – 6x2 + 11x– 6, то при делении получим
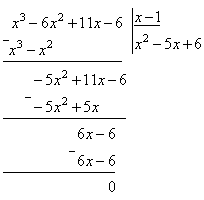

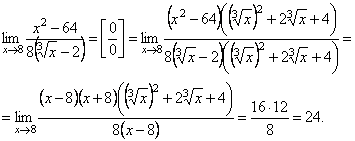
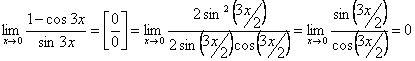 .
.
II. Неопределенность
![]() .
.
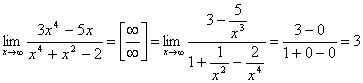 .
.
При вычислении предела числитель и знаменатель данной дроби разделили на x в старшей степени.
2.
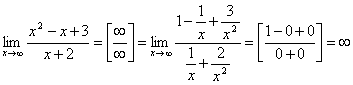
3.
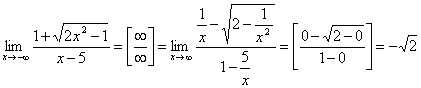 .
.
При
вычислении предела воспользовались
равенством
![]() ,
если x<0.
,
если x<0.
Следующие виды неопределенностей с помощью алгебраических преобразований функции, стоящей под знаком предела, сводят к одному из рассмотренных выше случаев или .
III. Неопределенность 0 ·∞.
![]() .
.
IV. Неопределенность ∞ –∞.
1.

2.
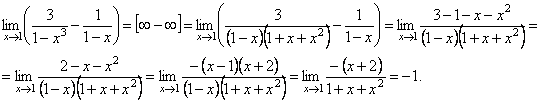
3.
![]() .
.
ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ.
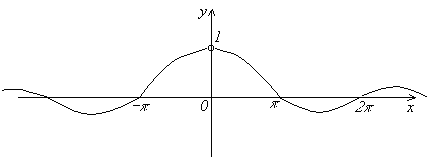
Функция
![]() не
определена при x=0, так как числитель
и знаменатель дроби обращаются в нуль.
График функции изображен на рисунке.
не
определена при x=0, так как числитель
и знаменатель дроби обращаются в нуль.
График функции изображен на рисунке.
Однако, можно найти предел этой функции при х→0.
![]()
Приведем доказательство записанной
формулы. Рассмотрим окружность радиуса
1 и предполож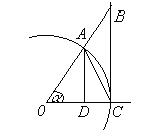 им,
что угол α, выраженный в радианах,
заключен в пределах 0 < α < π/2. (Так как
им,
что угол α, выраженный в радианах,
заключен в пределах 0 < α < π/2. (Так как
![]() четная
функция и ее значения не изменяются при
изменении знака α, то достаточно
рассмотреть случай, когда α > 0.) Из
рисунка видно, что SΔOAC
<Sсект.OAC <SΔOBC.
четная
функция и ее значения не изменяются при
изменении знака α, то достаточно
рассмотреть случай, когда α > 0.) Из
рисунка видно, что SΔOAC
<Sсект.OAC <SΔOBC.
Так как указанные площади соответственно равны
SΔOAC=0,5∙OC∙OA∙sinα=0,5sinα,Sсект.OAC=0,5∙OC2∙α=0,5α,SΔOBC=0,5∙OC∙BC=0,5tgα.
Следовательно, sin α < α < tg α.
Разделим все члены неравенства на sin α > 0:
![]() .
.
Но
![]() .
Поэтому на основании теоремы 4 о пределах
заключаем, что
.
Поэтому на основании теоремы 4 о пределах
заключаем, что
![]() .
.
Выведенная формула и называется первым замечательным пределом.
Таким образом, первый замечательный
предел служит для раскрытия неопределенности
.
Заметим, что полученную формулу не
следует путать с пределами
![]() .
.
Примеры.
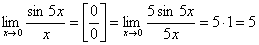 .
.
2.
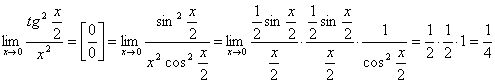 .
.
3.
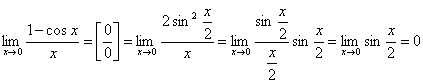 .
.
4.
![]() .
.
5.
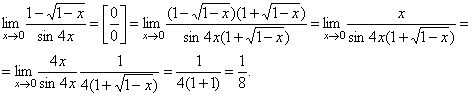
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ. Второй
замечательный предел служит для раскрытия
неопределенности 1∞ и выглядит
следующим образом
![]()
Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).
Примеры.
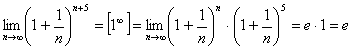 .
.
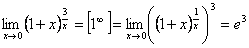 .
.
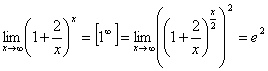 .
.
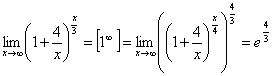 .
.
 .
.
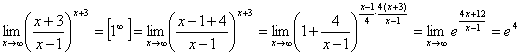 .
.
СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ. Пусть при x→a функции f(x) и g(x) являются бесконечно малыми. Тогда будем пользоваться следующими определениями.
Если
 ,
то f(x) называется бесконечно малой
высшего порядка, чем g(x) (относительно
g(x)).
,
то f(x) называется бесконечно малой
высшего порядка, чем g(x) (относительно
g(x)).
Если
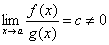 ,
то функции f(x) и g(x) называются
бесконечно малыми одногопорядка.
,
то функции f(x) и g(x) называются
бесконечно малыми одногопорядка.
Если
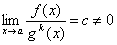 ,
то f(x) называется бесконечно малой
k-го порядка относительноg(x).
,
то f(x) называется бесконечно малой
k-го порядка относительноg(x).
Если
![]() ,
то функции f(x) и g(x) называются
эквивалентными бесконечно малыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначать f ≈ g.
,
то функции f(x) и g(x) называются
эквивалентными бесконечно малыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначать f ≈ g.
Примеры.
Пусть f(x)=x2,g(x)=5x. Функции являются бесконечно малыми при x→0. Найдем
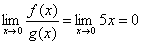 .
Следовательно, f(x) – бесконечно
малая высшего порядка относительно
g(x).
.
Следовательно, f(x) – бесконечно
малая высшего порядка относительно
g(x).
Пусть f(x)=x2–4,g(x)=x2–5x+6 – бесконечно малые при x→2.
![]() .
.
Поэтому f(x) и g(x) одного порядка.
f(x)=tg2x,g(x) = 2x – бесконечно малые при х→0.
![]() .
.
Следовательно, f ≈ g.
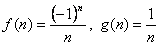 –
бесконечно малые при n→∞.
–
бесконечно малые при n→∞.
![]() –
этот предел не существует. Поэтому
говорят, что функции f и g не
сравнимы.
–
этот предел не существует. Поэтому
говорят, что функции f и g не
сравнимы.
При вычислении пределов полезно помнить о следующем свойстве эквивалентных бесконечно малых функций.
Теорема. Пусть f и g – бесконечно
малые функции при х→а. Если
![]() и
f ≈ f1, g ≈ g1, то
и
f ≈ f1, g ≈ g1, то
![]() ,
т.е. если отношение двух бесконечно
малых имеет предел, то этот предел не
изменится, если каждую из бесконечно
малых заменить эквивалентной бесконечно
малой.
,
т.е. если отношение двух бесконечно
малых имеет предел, то этот предел не
изменится, если каждую из бесконечно
малых заменить эквивалентной бесконечно
малой.
Доказательство. Имеем
![]() .
Тогда
.
Тогда
![]() ,
,
что и требовалось доказать.
Докажите самостоятельно эквивалентность следующих бесконечно малых функций при
x→0: sinx ≈ x,tgx ≈ x,arcsinx ≈ x,arctgx ≈ x,1–cosx ≈ x2∕2,loga(1+x) ≈ x/lna,ln (1+x) ≈ x,(1+x)m–1 ≈ mx,ax–1 ≈ xlna,ex–1 ≈ x.
Примеры.
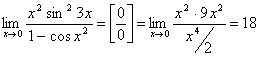 .
.

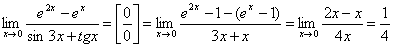 .
.
НЕПРЕРЫВНЫЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ.
Представление о непрерывности функции
интуитивно связано у нас с тем, что её
графиком является плавная, нигде не
прерывающаяся линия. При рассмотрении
графика такой функции y = f(x) мы видим,
что близким значениям аргумента
соответствуют б лизкие
значения функции: если независимая
переменная
лизкие
значения функции: если независимая
переменная
![]() приближается
к точке x0, то значение
функции y = f(x) неограниченно
приближается к значению функции в
точкеx0, т.е. к f(x0).
приближается
к точке x0, то значение
функции y = f(x) неограниченно
приближается к значению функции в
точкеx0, т.е. к f(x0).
Дадим строгое определение непрерывности функции. Итак, пусть имеем функцию y = f(x).
Функция y = f(x) называется непрерывной в точке x0, если она определена в этой точке и в некоторой окрестности содержащей x0 и
|
(1) |
Таким образом, можно сказать, что функция непрерывна в точкеx0, если выполнены 3 условия:
она определена в точке x0 и в некоторой её окрестности;
имеет предел при x → x0;
этот предел равен значению функции в точке x0.
Формулу (1) можно записать в виде
![]() ,
т.к.
,
т.к.
![]() .
Это означает, что для того, чтобы найти
предел непрерывной функции при x →
x0, достаточно в выражение
функции подставить вместо аргумента
xего значение x0.
.
Это означает, что для того, чтобы найти
предел непрерывной функции при x →
x0, достаточно в выражение
функции подставить вместо аргумента
xего значение x0.
Пример: Докажем, что функция y =
3x2 непрерывна в произвольной
точке x0. Для этого найдем
![]() .
.
Если функция y=f(x) непрерывна в каждой точке некоторого интервала (a; b), где a < b, то говорят, что функция непрерывна на этом интервале.
Непрерывные функции обладают следующими свойствами.
Теорема 1. Если функции f(x) и g(x) непрерывны в точке x0, то их сумма φ(x) = f(x) + g(x) также есть непрерывная функция в точке x0.
Доказательство. Так как функции
f(x) и g(x) непрерывны в точке x0,
то исходя из определения можно написать
![]() .
Тогда на основании свойств пределов
будем иметь
.
Тогда на основании свойств пределов
будем иметь
![]() .
.
Эта теорема справедлива для любого конечного числа слагаемых.
Следующие две теоремы докажите самостоятельно аналогично теореме 1.
Теорема 2. Произведение двух непрерывных функций есть функция непрерывная.
Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.
Если функцию можно представить в виде
y = f(u), где u = φ(x), т.е. если функция
![]() зависит
от переменной
через
промежуточный аргумент u, то
называется
сложной функцией переменной x.
зависит
от переменной
через
промежуточный аргумент u, то
называется
сложной функцией переменной x.
Примеры:
y = sinx3. Здесь u = x3, y = sin u.
y = etg x, u = tg x, y = eu.
Таким образом, под термином сложная функция следует понимать не какое – либо очень сложное выражение, а функцию, которая зависит от аргумента x через несколько промежуточных функций.
Справедлива следующая ТЕОРЕМА.
Теорема 4. Если функция u = φ(x) непрерывна в точкеx0 и принимает в этой точке значение u0 = φ(x0), а функция f(u) непрерывна в точке u0, то сложная функция y = f(φ(x)) непрерывна в точке x0.
Используя эти теоремы можно доказать следующий результат.
Теорема 5. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Заметим, что если функция y = f(x) непрерывна в точке x0 и её значение в этой точке отлично от 0, f(x0) ≠ 0, то значения функции f(x) в некоторой окрестности точки x0 имеют тот же знак, что и f(x0), т.е. если f(x0) > 0, то найдётся такое δ > 0, что на интервале(x0– δ;x0+ δ) f(x) > 0 (в этой окрестности значения функции f(x) очень мало отличаются от своего предела).
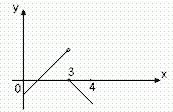
ТОЧКИ РАЗРЫВА И ИХ КЛАССИФИКАЦИЯ. Если
рассмотреть график функции
![]() в
окрестности точки x= 0 (см. рис. справа),
то ясно видно, что он как бы “разрывается”
на отдельные кривые. Аналогично можно
рассмотреть функцию, изображенную на
рисунке слева в окрестности точки 3.
Говорят, что во всех указанных точках
соответствующие функции становятся
разрывными.
в
окрестности точки x= 0 (см. рис. справа),
то ясно видно, что он как бы “разрывается”
на отдельные кривые. Аналогично можно
рассмотреть функцию, изображенную на
рисунке слева в окрестности точки 3.
Говорят, что во всех указанных точках
соответствующие функции становятся
разрывными.

Точка
![]() называется
точкой разрыва функции y = f(x),
если она принадлежит области определения
функции или её границе и не является
точкой непрерывности. В этом случае
говорят, что при x= x0 функция
разрывна. Это может произойти, если в
точке x0 функция не определена
или не существует предел
называется
точкой разрыва функции y = f(x),
если она принадлежит области определения
функции или её границе и не является
точкой непрерывности. В этом случае
говорят, что при x= x0 функция
разрывна. Это может произойти, если в
точке x0 функция не определена
или не существует предел
![]() ,
или если предел существует, но
,
или если предел существует, но
![]() .
.
Примеры.
Рассмотрим функцию:
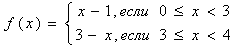
Эта функция определена во всех точках отрезка [0, 4] и её значение при x = 3 равно 0. Однако, в точке x = 3 функция имеет разрыв, т.к. она не имеет предела при x = 3:
![]()
Следует отметить, что f(x) непрерывна во всех остальных точках отрезка [0, 4]. При этом в точке x = 0 она непрерывна справа, а в точке x = 4 – слева, т.к.
![]() .
.
Как уже отмечалось, функция разрывна при x = 0. Действительно, при x = 0 функция не определена:
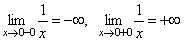 .
.
Ф
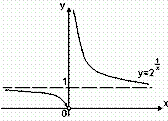 ункция
ункция
 разрывна
при x = 0. Действительно,
разрывна
при x = 0. Действительно,
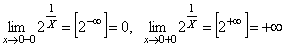 .
При x = 0 функция не определена.
.
При x = 0 функция не определена.
Функция
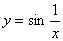 определена
для всех значений x, кроме x = 0.
В этой точке она имеет разрыв, т.к. предел
не существует (рисунок см. в предыдущей
лекции ).
определена
для всех значений x, кроме x = 0.
В этой точке она имеет разрыв, т.к. предел
не существует (рисунок см. в предыдущей
лекции ).
Точки разрыва функции можно разбить
на два типа. Точка разрыва x0
функции f(x) называется точкой
разрыва первого рода, если существуют
оба односторонних конечных предела
![]() и
и
![]() ,
но они не равны между собой или не равны
значению функции в точке x0,
т.е. f(x0). Точка разрыва,
не являющаяся точкой разрыва первого
рода, называется точкой разрыва второго
рода.
,
но они не равны между собой или не равны
значению функции в точке x0,
т.е. f(x0). Точка разрыва,
не являющаяся точкой разрыва первого
рода, называется точкой разрыва второго
рода.
Примеры: В первом примере точка х=3 является точкой разрыва первого рода. В примерах 2 – 4 все точки разрыва являются точками разрыва второго рода.
Д
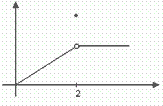 ля
функции, изображённой на рисунке точка
x = 2 является точкой разрыва первого
рода.
ля
функции, изображённой на рисунке точка
x = 2 является точкой разрыва первого
рода.
Функция
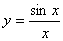 не
определена в точке x = 0. Эта точка
является точкой разрыва 1-го рода, т.к.
в ней существуют пределы справа и слева.
не
определена в точке x = 0. Эта точка
является точкой разрыва 1-го рода, т.к.
в ней существуют пределы справа и слева.
СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ. Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.
Функцию y = f(x) называют непрерывной
на отрезке [a, b], если она
непрерывна во всех внутренних т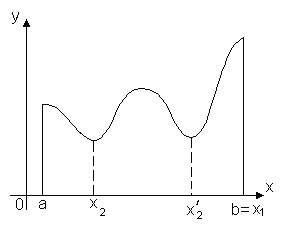 очках
этого отрезка, а на его концах, т.е. в
точках a и b, непрерывна
соответственно справа и слева.
очках
этого отрезка, а на его концах, т.е. в
точках a и b, непрерывна
соответственно справа и слева.
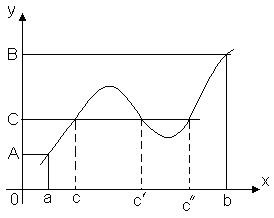
Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.
Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x1 [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).
Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x2 и x2'.
Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.
Также теорема перестаёт быть верной для разрывных функций. Приведите пример.
Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.
Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать. Эта теорема допускает следующее обобщение. Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C. Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C. Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности: Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями. |
|
ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке.
 Для каждого значения аргумента xиз
этого промежутка функция y=f(x) имеет
определенное значение.
Для каждого значения аргумента xиз
этого промежутка функция y=f(x) имеет
определенное значение.
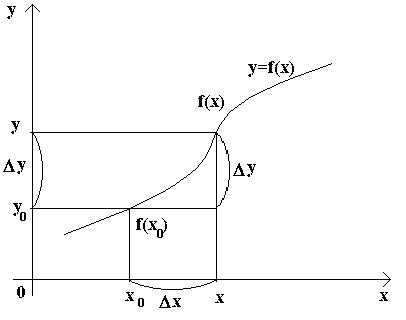
Рассмотрим два значения аргумента: исходное x0 и новое x. Разность x– x0 называется приращением аргумента x в точке x0 и обозначается Δx. Таким образом, Δx = x – x0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x0+Δx, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x0 значение функции было f(x0), то в новой точке x функция будет принимать значение f(x) = f(x0 +Δx).
Разность y – y0 = f(x) – f(x0) называется приращением функции y = f(x) в точке x0 и обозначается символом Δy. Таким образом, Δy = f(x) – f(x0) = f(x0 +Δx) - f(x0).
Обычно исходное значение аргумента x0 считается фиксированным, а новое значение x – переменным. Тогда y0 = f(x0) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δxтакже будут переменными и формула (1) показывает, что Dy является функцией переменной Δx.
Составим отношение приращения функции к приращению аргумента
![]()
Найдем предел этого отношения при Δx→0. Если этот предел существует, то его называют производной данной функции f(x) в точке x0 и обозначают f '(x0). Итак,
![]() .
.
Производной данной функции y = f(x) в точке x0 называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю.
Заметим, что для одной и той же функции
производная в различных точках xможет
принимать различные значения, т.е.
производную можно рассматривать как
функцию аргумента x. Эта функция
обозначается f '(x). Производная
обозначается символами f '(x),y ',
![]() .
Конкретное значение производной при x
= aобозначается f '(a) или y
'|x=a.
.
Конкретное значение производной при x
= aобозначается f '(a) или y
'|x=a.
Операция нахождения производной от функции f(x) называется дифференцированием этой функции. Для непосредственного нахождения производной по определению можно применить следующее практическое правило:
Придать x приращение Δx и найти наращенное значение функции f(x + Δx).
Найти приращение функции Δy = f(x + Δx) – f(x).
Составить отношение
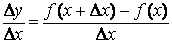 и
найти предел этого отношения при Δx∞0.
и
найти предел этого отношения при Δx∞0.
Пример.Найти производную функции
y = x2 а) в произвольной
точке; б) в точке x= 2.Решение.
а) f(x + Δx) = (x + Δx)2; Δy = (x + Δx)2
– x2=2xΔx– x2;
![]() .
б) f '(2) = 4
.
б) f '(2) = 4
Пример.
Используя определение найти производную
функции
![]() в
произвольной точке. Решение. Шаг1)
в
произвольной точке. Решение. Шаг1)
![]() .
Шаг 2)
.
Шаг 2)![]()
Шаг 3)
![]() .
.
МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения. Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени. Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).
Отметим некоторый момент времени t0. К этому моменту точка прошла путь s=s(t0). Определим скорость v материальной точки в момент времени t0.
Для этого рассмотрим какой-нибудь другой момент времени t0+Δt. Ему соответствует пройденный путь s=s(t0+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t0+Δt)–s(t).
Рассмотрим отношение
![]() .
Оно называется средней скоростью в
промежутке времени Δt. Средняя
скорость не может точно охарактеризовать
быстроту перемещения точки в момент t0
(т.к. движение неравномерно). Для того,
чтобы точнее выразить эту истинную
скорость с помощью средней скорости,
нужно взять меньший промежуток времени
Δt.
.
Оно называется средней скоростью в
промежутке времени Δt. Средняя
скорость не может точно охарактеризовать
быстроту перемещения точки в момент t0
(т.к. движение неравномерно). Для того,
чтобы точнее выразить эту истинную
скорость с помощью средней скорости,
нужно взять меньший промежуток времени
Δt.
Итак, скоростью движения в данный момент
времени t0 (мгновенной скоростью)
называется предел средней скорости в
промежутке от t0 до t0+Δt,
когда Δt→0:
![]() ,
т.е. скорость неравномерного движения
это производная от пройденного пути по
времени.
,
т.е. скорость неравномерного движения
это производная от пройденного пути по
времени.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. Введем сначала определение касательной к кривой в данной точке.
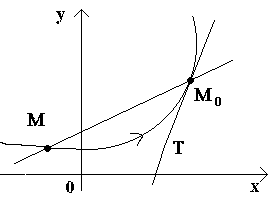
Пусть имеем кривую и на ней фиксированную точку М0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M0M. Если точка М начинает перемещаться по кривой, а точка М0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М0 с любой стороны секущая стремится занять положение определенной прямой М0Т, то прямая М0Т называется касательной к кривой в данной точке М0.
Т.о., касательной к кривой в данной точке М0 называется предельное положение секущей М0М, когда точка М стремится вдоль кривой к точке М0.
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х0 функция принимает значение y0=f(x0). Этим значениям x0 и y0 на кривой соответствует точка М0(x0; y0).
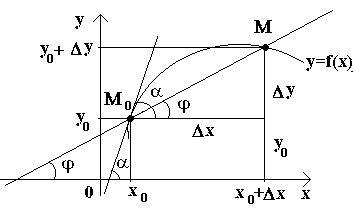 Дадим
аргументу x0 приращение
Δх. Новому значению аргумента
соответствует наращенное значение
функции y0+Δ y. Получаем
точку М(x0+Δx; y0+Δy).
Проведем секущую М0М
и обозначим через φ угол, образованный
секущей с положительным направлением
оси Ox. Составим отношение
Дадим
аргументу x0 приращение
Δх. Новому значению аргумента
соответствует наращенное значение
функции y0+Δ y. Получаем
точку М(x0+Δx; y0+Δy).
Проведем секущую М0М
и обозначим через φ угол, образованный
секущей с положительным направлением
оси Ox. Составим отношение
![]() и
заметим, что
и
заметим, что
![]() .
.
Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М0. Тогда секущая М0М будет стремиться занять положение касательной к кривой в точке М0, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:
![]() ,
т.е. f '(x) = tg α .
,
т.е. f '(x) = tg α .
Т.о., геометрически у'(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0, т.е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М0 (x; y) с положительным направлением оси Ox.
Пример. Найти угловой коэффициент касательной к кривой у = х2 в точке М(-1; 1). Ранее мы уже видели, что (x2)' = 2х. Но угловой коэффициент касательной к кривой есть tg α = y'|x=-1 = – 2.
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ
Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом, из дифференцируемости функции следует ее непрерывность.
Доказательство. Если
![]() ,
то
,
то
![]() ,
где α бесконечно малая величина, т.е.
величина, стремящаяся к нулю при Δx→0.
,
где α бесконечно малая величина, т.е.
величина, стремящаяся к нулю при Δx→0.
Но тогда Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Таким образом, в точках разрыва функция
не может иметь производной. Обратное
утверждение неверно: существуют
непрерывные функции, которые в некоторых
точках не являются дифференцируемыми
(т.е. не имеют в этих точках производной).
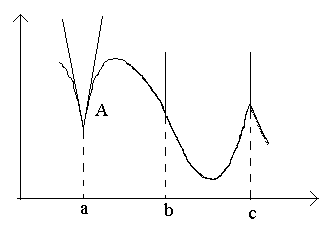
Рассмотрим на рисунке точки а, b, c. В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к1 и к2. Такой тип точек называют угловыми точками.
В точке b при Δx→0 отношение
является
знакопостоянной бесконечно большой
величиной
![]() .
Функция имеет бесконечную производную.
В этой точке график имеет вертикальную
касательную. Тип точки – "точка
перегиба" c вертикальной касательной.
.
Функция имеет бесконечную производную.
В этой точке график имеет вертикальную
касательную. Тип точки – "точка
перегиба" c вертикальной касательной.
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.
Примеры.
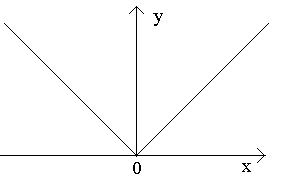
Р
 ассмотрим
функцию y=|x|.Эта функция непрерывна
в точке x = 0, т.к.
ассмотрим
функцию y=|x|.Эта функция непрерывна
в точке x = 0, т.к.
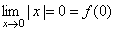 .
.
Покажем, что она не имеет производной в этой точке. f(0+Δx) = f(Δx) = |Δx|. Следовательно, Δy = f(Δx) – f(0) = |Δx|
Но тогда при Δx< 0 (т.е. при Δx
стремящемся к 0 слева)
![]() А
при Δx > 0
А
при Δx > 0
![]() .
Т.о., отношение
при
Δx→ 0 справа и слева имеет различные
пределы, а это значит, что отношение
предела не имеет, т.е. производная функции
y=|x| в точке x= 0 не существует.
Геометрически это значит, что в точке
x= 0 данная "кривая" не имеет
определенной касательной (в этой точке
их две).
.
Т.о., отношение
при
Δx→ 0 справа и слева имеет различные
пределы, а это значит, что отношение
предела не имеет, т.е. производная функции
y=|x| в точке x= 0 не существует.
Геометрически это значит, что в точке
x= 0 данная "кривая" не имеет
определенной касательной (в этой точке
их две).
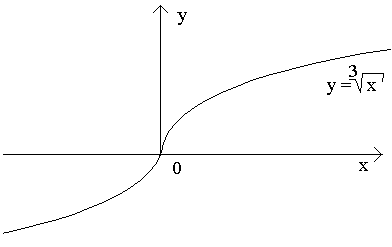
Функция
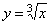 определена
и непрерывна на всей числовой прямой.
Выясним, имеет ли эта функция производную
при x= 0.
определена
и непрерывна на всей числовой прямой.
Выясним, имеет ли эта функция производную
при x= 0.
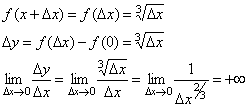
Следовательно, рассматриваемая функция
не дифференцируема в точке x= 0.
Касательная к кривой в этой точке
образует с осью абсцисс угол
![]() /2,
т.е. совпадает с осью Oy.
/2,
т.е. совпадает с осью Oy.


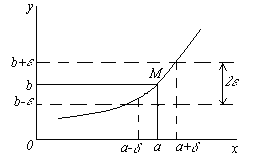 рис.
к примеру 1
рис.
к примеру 1