2. Метод Фибоначчи.

Последовательность чисел Фибоначчи определяется соотношением:

(8)

и имеет вид:

Подобно методу золотого сечения процедура поиска с использованием чисел Фибоначчи требует два вычисления функции на первом шаге, а на каждом последующем - только по одному. Однако, в отличие от метода золотого сечения, в этой процедуре общее число S вычисления функции должно быть выбрано заранее. Кроме того, сокращение интервала неопределенности не остается постоянным, а меняется от шага к шагу: на k-ом шаге длина интервала неопределенности сжимается с коэффициентом

Первые два вычисления проводятся в точках:

расположенных симметрично относительно середины отрезка [a,b]. Если f(x1)<f(x2), то новым отрезком локализации минимума является [a, x2], в случае f(x1)≥f(x2)-[x1, b]. Каждая следующая точка выбирается симметрично относительно середины полученного отрезка к лежащей внутри этого отрезка точке уже проведенного вычисления (x1 или x2). При этом любая внутренняя точка делит отрезок локализации в отношении, двух последовательных чисел Фибоначчи.

В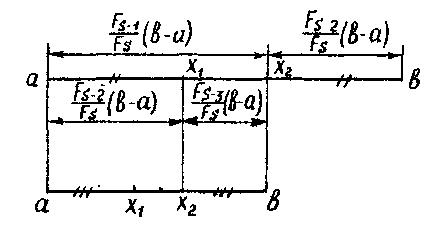 заимное расположение точек первых трех вычислений в случае f(x1)<f(x2) показано на рис. 7.

Первый шаг

Второй шаг

Рис. 7.

После (S-1)-го шага точка проведенного вычисления оказывается в середине отрезка локализации. Точка последнего, S-го, шага выбирается на расстоянии δ от середины этого отрезка, где δ - заранее фиксированное малое положительное число (константа различимости).

После S вычислений функции длина отрезка локализации составляет (с точностью до δ):

(9)

Сравнение (9) и (7) показывает, что при одном и том же S метод Фибоначчи дает меньший интервал неопределенности, чем метод золотого сечения, т.е. является более эффективным. Однако для достаточно больших S значение стремится к (0,618)S-1 , так что эти методы становятся почти идентичными.

В том случае; когда при использовании метода Фибоначчи задан .конечный интервал неопределенности ε, число S можно определить из условия:

(10)

Алгоритм минимизации функции f(x) с использование, чисел Фибоначчи.

1. По заданной точности рассчитывается вспомогательное число

2. Для полученного значения N находится такое число Фибоначчи FS, для которого выполняется неравенство:

3.

4. По формуле (9) определяется длина конечного интервала неопределенности l.

5. Вычисляются значения x1=a+l∙FS-2, x2=b-l∙FS-2.

6. В зависимости от соотношения f(x1) и f(x2) выбирается новый интервал локализации минимума.

7. Внутри полученного интервала находится новая точка (x1 или x2), симметричная к уже имеющейся точке и отстоящая от конца интервала на величину l∙FS-1-k , где k - номер шага. В этой точке рассчитывается значение f(x). Затем вычисления повторяются, начиная с пункта 5, до тех пор, пока k не станет равно S-1. Тогда переходят к пункту 7.

8. Полагают x2=x1+δ, находят f(x2). Если f(x2)>f(x1)то минимум реализуется на интервале (a, x1), в противном случае - на интервале (x1 , b).

Блок-схема описанного алгоритма приведена на рис.8.

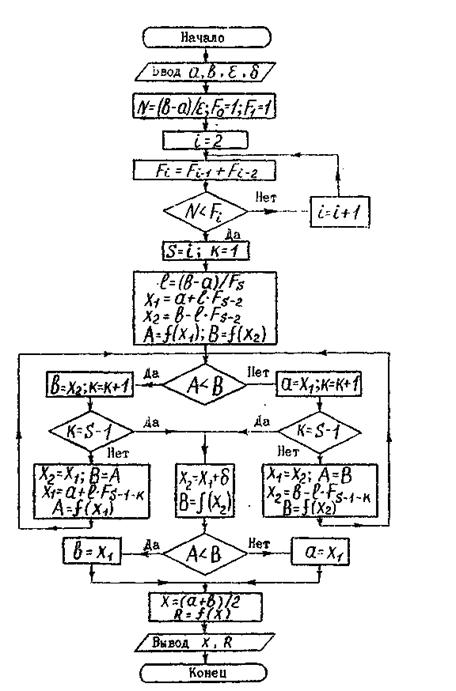
Рис. 8. Блок – схема алгоритма поиска минимума функции f(x) использованием чисел Фибоначчи