19. Одм. Ряд распр-я, многоугольник распр-я.

Для более наглядного представл. Строят граф. Изображение ряда распр-я:

-по оси абсцисс откладыв. Возможн. Знач-я случ. величины

-по оси ординат – их вер-ти

-получ. точки соедин. отрезком прямых. Такая фигура наз. многоугольником распр-я.

Рассмотренные формы задания з-на распр-я применимы для дискретной случ. величины.

Для описания непрерывной случ. величины вводят понятие функции распр-я.

20. Одм.Функ-я распр-я случ. Величины и ее св-ва

Функ-ей рапр-я случ. величины Х наз-т вер-ть события, знач-е случ. величины, полученное в рез-те опыта будет меньше некот-го Х.F(X)=P(X<x)

F(X) наз. также интеграл. Функцией или интегральным з-ном распр-я.

Функция распр-я наиболее универс. хар-ка случ. величины, она полностью характ. случ. величину с вероятн. точки зрения и сущ. для дисперсн. и для непрерывных случ. величин.

Свойства функции распр-я

1. F(Х) неубыв. Функ-я своего аргумента, т.е. если Х₁>X₂, то F(Х₂)> F(Х₁);

2. на - функ-я распр-я равна 0: F(- )=0

3. на + функ-я распр-я равна 1: F(+ )=1

При реш-и практич. Задач часто необх-мо опред. вер-ть того, что случ. величина примет знач-е в диапазоне от Из опред-я функ-и распр-я следует , что искомую вер-ть следует найти из уравн-я

График функ-и распред-я в общем случ. представляет собой график неубыв.функ-и, знач-я кот-й лежат в диапазоне от 0 до 1 , при чем в отдельных точкой функ-я может иметь разрывы , скачки

Ф-ция распр-я дискретной случ. величины- разрывная ступенчатая ф-ция скачки кот-й происходят в точках соотв. возможным знач-ям случ. величины и равны вер-тям этих знач-й, сумма всех скачков равна 1.

По мере увеличения числа возм-х знач-й случ. величина и по мере уменьшения интервалов между ними число скачков становиться больше, а их величина меньше, ступенчатая кривая становится более плавной, ступенчатая величина постоянно приближается к непрерывной.

Для реш-я многих практ. задач удобно пользоваться др. формой предст. з-на распр-я – плотностью

распр-я.

21. Одм. Плотность распр-я случ. Величины и ее св-ва

Плотность распр-я не явл. универс. хар-кой случ. величины, она сущ. только для непрерывн. случ. величин и опр. как производная от функ-и распр-я

наз. также дифференц. Функ-ей распр-я или диф. З-ном распр-явеличины Х.

Функ-я рапр-я может быть выражена через плотность

Кривая, изобр. Плотность распр-я случ.величины наз. кривой распр-я.

Площадь под этой кривой,лежащая левее вертикали, проведенной через точку Х, равна знач-ю функ-и F(X)

Cвойства плотности распр-я:

1. плотность распр-я есть неотриц. функ-я f(x)>0 . Это св-во следует из того, что функ-я распр-я F(X) есть неубыв. ф-цией.

2. интеграл в бесконечных пределах от плотности распр-я =1 это следует из того, что F(+ )=1. Геом. Осн. Св-ва плотности распр-я означ. , что :

1. всякривая распределения лежит не ниже оси абсцисс

2. полная площадь, ограниченная кривой распр-я и осью абсцисс равна 1.

Геом. Вер-ть, попадания вел. Х на участкок ( ) равна площади под кривой распре-я, опирающейся на этот участок.

22. ОДМ. Числовые хар-ки случ. величины: матожидание, мода, медиана Среди числовых хар-к случайных величин прежде всего отвечают те, кот-е определяют положение случайной величины на числовой оси,т.е. указывают некот-е ориентировочное значение около кот-го группируются все возможные значения случайной величины.Из хар-к положения важную роль играет мат. ожидание.Рассмотрим дискретную случайную величину , кот-я в рез-те опыта приняла знач-е Х₁,Х₂,..,Х_n с вероятностями р₁,р₂,…,р_n. Требуется охаракт. Каким-то числом положение случайной величины на оси абсцисс с учетом того, что эти знач-я имеют разные вероятности. Для этой цели можно воспользоваться средним взвешенным, т.е. каждое знач-е Х_i при осреднении должно учитываться с весом пропорциональным его вер-ти:

Это среднее взвешенное знач-е и называется мат. Ожиданием случайной величины М[Х].

Мат. ожидание связано со средним арифметическим.При большом числе наблюд. знач-й случайной величины приближается(сходиться) по вертикале к ее мат. ожиданию,т.о. среднее арифм. знач-е явл. статической оценкой мат. ожидания. Пусть производиться N независ. опытов, в каждом из кот-х случайная величина Х принимает опред. знач-е при чем знач-е Х₁ m₁ раз, Х₂ m₂ раз и т.д. Очевидно, что сумма по m :

Среднее арифметическое наблюд. знач-й случайной величины произведение всех знач-й случайной величины на их частоты.

При увеличении числа опытов N частоты р_* будут приближаться к соотв. вер-тям, среднее ариф. наблюдаемых знач-й случайной величиныпри уменьшении числа опытов будет приближаться к ее мат. ожиданию.

Выражение (*) было получено для дискретной случайной величины. Для непрерывной случайной величины мат. ожидание определяется интегралом:

где f(x)-плотность распределения величины Х.

Кроме мат. ожидания применяют и др. хар-ки положения, например, мода и медиана. Модой дискретной случайной величины наз. ее наиболее вероятное знач-е, для непрерывной случайной величины модой явл. то знач-е, в кот-м плотность вер-тей максимальна. Если кривая распределения имеет более одного максимума, то такое распределение наз. полимодальным.

Иногда встречаются распределения не максимальным, минимальным, такие распределения наз. антимодальными. Мода и мат. ожидания не совпадают, однако в случае симметричного распр-я мат. ожидание,если оно существует, оно совпадает с модой, если она существует, и центром симметричного распр-я. Медианой случайной величины Х наз. такое ее знач-е, для кот-го одинаково вероятно окажется ли случайная величина больше или меньше медианы.

Геометрическая медиана- это абсцисса точки, вертикаль, проведенная через кот-ю, делит площадь, ограниченную кривой распред-я пополам.

В случае симметричного модального распред-я

медиана совпадает с модой и мат. ожиданием.

Для описания основных св-в случ величины применяют моменты 2-х видов:начальные и центральные. Начальным мометом порядка k дискретной случайной величины Х

наз. сумма вида :

.

23.ОДМ. Начальные моменты случ. величины Для непрерывной случайной величины Х k-начальный момент задается интервалом

Основная хар-ка положения мат. ожидания

Представляет 1 начальный момент случайной величины. Пользуясь знаком мат. ожидания можно определить формулы, для дискретных и непрерывных случайных величин и записать общее опред-е начального момента k-го порядка

Т.е. начальный момент k-го порядка случайной величины Х наз. мат. ожиданием k-степени этой случайной величины.

24. ОДМ. Центральные моменты случ.величины Вводим назв-е центрируемой величины Х с ожиданием m_{x .}

Центрируемой случ. величиной наз. отклонение Х от ее мат. ожидания.

Центр. моментом порядка k величины Х наз. мат. ожидание k-й степени соотв. центрирующей случайной величины

Для дискр. случ. величины:

Для непрерывн. случ. величины:

Мат. ожидание центр. случ. величины-это центр. момент 1 порядка и =0.

Второй центр. момент-дисперсия случ. величины:

Д[Х]=M[ ]

Дисперсия-это мат. ожидание квадрата центр. случ. величины.

Дисперсия-хар-ка рассеивания.

Дисперсия случ. величины имеет знач-е квадрата случ. величины, но удобней пользоваться величиной, размерность кот-й совпадает с размерностью величины Х. Для этого из дисперсии извлекают квадратный корень. Полученная величина наз. средним квадратическим отклонением и обозначается .

25.ОДМ. Понятие эксцесса и скошенности Для хар-ки ассиметрии, скошенности распр-я служит 3 ценр. момент. Если распределение симметрично отн. мат. ожидания, то все моменты нечетного порядка, если они сущ., то они =0. Поэтому в качестве хар-ки ассиметрии распред-я выбирают нечент. момент. Полученная величина носит название коэффициента ассиметрии, обозначается

Хар-кой крутости или остро- или плосковершинности распр-я служит 4 ценр. момент. Для получения безразмерной хар-ки вводят понятие эксцесса.

Эксцессом случ. величины Х наз. соотн-е

Число 3 вычитается потому что для широкораспростр. Нормального з-на , кривые более островершинные по сравнению с норм. обладают положит. эксцессом, а кривые более плосковершинные по сравнению с норм. обладают положит. эксцессом.

26. ОДМ. Соотношение между начальными и центральными моментами различных порядков Выведем соотн-е между молекулами на дискретные случ. величины; аналогичное соотн-е справедливо и для непрерывных случ. величин , если заменить сумму интегралом, а вер-ти элементами вер-ти.

Для 2 центр. момента:

Для центр. момента 3 порядка:

Аналогично можно получить моменты для более высоких порядков.

27. ОДМ. Теоремы о числовых хар-ках: матожидание и дисперсия случ. величины;вынесение неслуч. Величины за знак матожидания и дисперсии Математ. ожидание неслучайной величины С равно самой неслучайной величине. М[C] = C.

Док-во: если рассм. неслучайную величину как частный вид случайной с одним возможным знач-ем вер-ть кот-го 1, то по опред-ю имеем М[C]=C*1=C

Дисперсия случайной величины равна 0. Д[C]=0

Док-во:

Неслучайную величину С можно вынести за знак мат. ожидания.

Неслучайную величину С можно вынести за знак дисперсии.

Можно вынести за знак дисперсии возводя ее в квадрат.

28. ОДМ. Теорема о матожидании суммы случ. величин Мат. ожидание суммы 2-х случайных величин равно сумме их мат. ожиданий (не обязательно 2 случ. величины, можно и больше)

М[X + Y]= M[X]+M[Y]

29.ОДМ. Теорема о матожидании линейной функ-и, теорема о дисперсии линейной функ-и независимых случ. величин Мат. ожидание линейной функции нескольких случ. элементов Х_i равно той же линейной функции от мат. ожиданий аргументов.

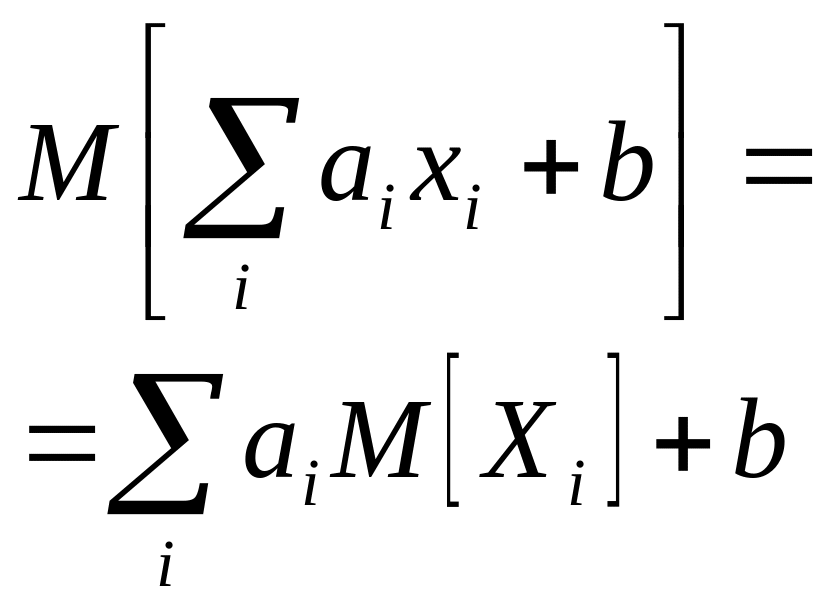
Док-во: пользуясь теоремой сложения мат. ожиданий и правилом вынесения мат. величины за знак мат. ожидания, получим:

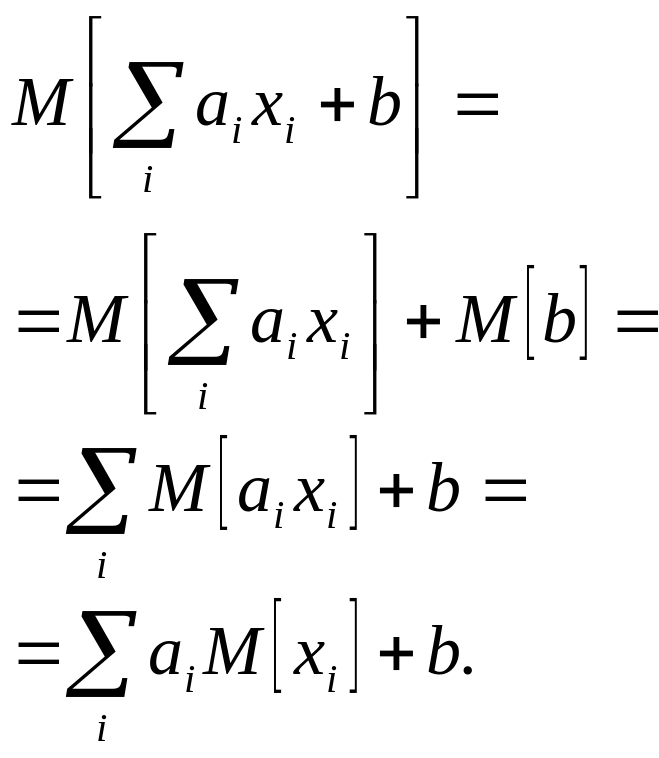
Дисперсия 2случ. величин = сумме их дисперсий + удвоенный корреляционный момент

Где К_XY - корреляционный, т.е. 1-й смешанный центр. момент случ. величин X, Y ? опред. из выр-я:

Фор-ла для дисперсии суммы может быть обобщена на любое число слагаемых. При этом если все случ.величины в сумме некоррелированы, дисперсия суммы = сумме дисперсий