7.Нейронные сети с нечеткой логикой

Методы символьной обработки информации не всегда позволяют получать удовлетворительное решение прикладных задач, особенно в условиях неполноты или недостаточной определенности исходных данных, что характерно для сложных технических устройств, систем экономического планирования, принятия решений и т.п. Выход состоит в использовании так называемых «мягких» вычислений, включающих нечеткую логику, теорию вероятности, нейрокомпьютинг и генетические алгоритмы. Эти составные части не конкурируют, а дополняют друг друга, создавая эффект взаимного усиления и реализуя так называемый «вычислительный интеллект». В рамках этого подхода НС с нечеткой логикой обучаются на базе универсального алгоритма, для которого необходима лишь достаточная по объему обучающая выборка, а результаты их работы, формируемые на базе систем нечеткого вывода, воспринимаются как ответы на вопросы «почему?».

7.1.Математические основы функционирования нечетких систем

Нечеткие множества (fuzzy sets) представляют собой обобщение обычных (четких) множеств (Л.Заде, 1965 г.). Степень принадлежности элемента х к множеству А характеризуется функцией принадлежности _А(х)[0,1], где _А(х)=0 означает отсутствие принадлежности, а _А(х)=1 – полную принадлежность, т.е. в нечетких системах элемент может частично [0<_А(х)<1] принадлежать к любому множеству. Конкретные значения _А(х) образуют коэффициенты (степени) принадлежности, которые задаются либо непрерывно (в виде некоторой функции), либо дискретно – в виде последовательности значений . Помимо цифровых переменных, в теории нечетких множеств существуют лингвистические переменные, которые аналогично обычным могут принимать различные лингвистические значения, например, экзаменационная оценка может быть «неудовлетворительной», «удовлетворительной», «хорошей» или «отличной» и это необязательно «2», «3», «4» или «5» соответственно.

Подобно «четким», на нечетких множествах могут быть определены аналогичные математические операции:

• логическая сумма множеств АВ

(7.1)

• логическое произведение множеств АВ

(7.2)

• отрицание множества

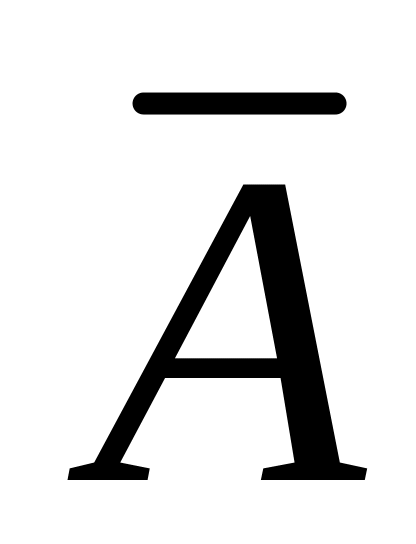
, (7.3)

которое в отличие от четкого, дает непустое множество с

• равенство множеств А и В, если _А(х_i)=_B(х_i);

• алгебраическое произведение множеств АВ

и т.д., (7.4)

причем эти операции также обладают свойствами ассоциативности, коммутативности и дистрибутивности. Из свойств нечетких множеств следует, что логическое произведение А и не обязательно образует пустое, а логическая сумма – полное множества, т.е.

(7.5)

Понятие нечеткости следует отличать от вероятности, определяемой отношением количества удачных попыток к общему их числу и применяющейся исключительно к оценке будущего. Нечеткость же определяется степенью принадлежности события х к некоторому множеству событий А и относится не только к прошлому, но и к настоящему и к будущему. Следует отметить, однако, что, если нечеткое понятие относится к будущему, то ему можно приписать некоторую вероятность (особенно при использовании лингвистических переменных).

7.2.Системы нечеткого вывода

Основное правило вывода – если х это А (предпосылка), то y это В (заключение), где А и В – значения лингвистических переменных, определяемые нечетким способом через соответствующие функции принадлежности, – называется нечеткой импликацией АВ. Получение заключения из множества правил «если–то» – нечеткое рассуждение – обычно принимает вид: если х₁ это А₁ и х₂ это А₂ и … и х_N это А_N, то y это В, где так же А_i_A(x_i), B_B(y). 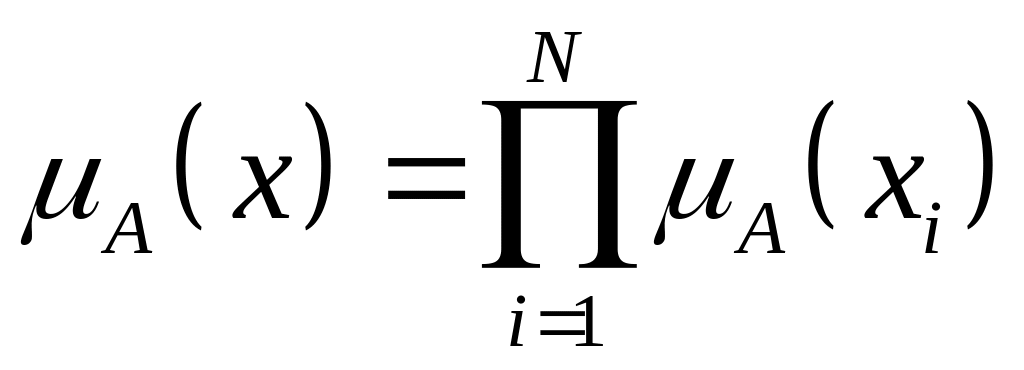Переход от многомерного условия x_iA_i к единственному значению функции принадлежности (агрегирование предпосылки) может осуществляться с помощью либо логического i=1,2,…,N, либо алгебраического произведений. Аналогично, каждой импликации АВ также можно приписать единственное значение функции принадлежности _AВ (x,y) в виде логического или алгебраического произведения (агрегирование на уровне импликации)

или (7.6)

Теория нечетких множеств, правила импликации и нечетких рассуждений образуют систему нечеткого вывода, в которой можно выделить:

• множество используемых нечетких правил;

• базу данных с описанием функций принадлежности;

• механизмы агрегирования и вывода на основе применяемых правил импликации.

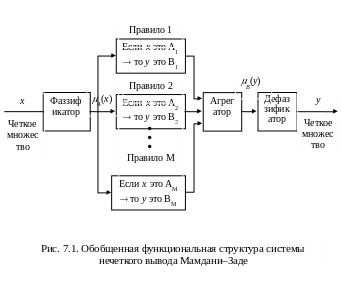
При технической реализации входные и выходные сигналы являются конкретными величинами, поэтому в состав нечеткой системы добавляют фаззификатор (преобразователь множества входных данных в нечеткое множество) на входе и дефаззификатор (преобразователь нечеткого множества в конкретное значение) на выходе. Обобщенная функциональная структура подобной системы (Мамдани–Заде), использующей М нечетких правил вывода, приведена на рис. 7.1. В этой весьма популярной для неадаптивных нечетких систем модели присутствуют следующие операторы:

• оператор «» или «» для определения результирующего значения _А(х) с учетом всех компонентов вектора условия или _АВ (х, y) для всей импликации АВ;

• оператор «» как агрегатор результатов импликации многих правил;

• оператор дефаззифиации нечеткого  (y) в четкое y.

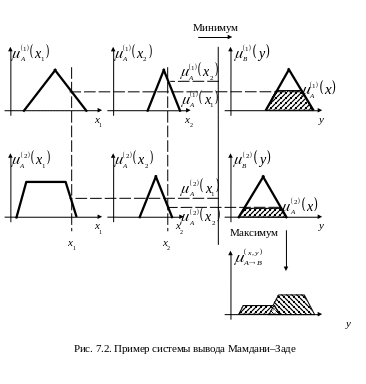
Пример использования системы вывода Мамдани–Заде для получения _АВ (х, y) при двух переменных х₁, х₂ и двух правилах нечеткого вывода с _А⁽¹⁾ (х) и _А⁽²⁾ (х) показан на рис. 7.2. Оператор «» (min) используется как для агрегирования нечетких правил относительно переменных х₁, х₂, так и на уровне импликации АВ для одиночных правил вывода. Агрегирование импликаций для совместного применения правил 1 и 2 использует оператор «» (max) с нечетким результатом в виде _АВ (х, y). Получение четкого значения y, соответствующее четким х₁ и х₂, требует применения процедуры дефаззификации.

Фаззификатор преобразует N – мерный входной вектор в нечеткое множество А с функцией принадлежности _А(х). С практической точки зрения в этом качестве наиболее популярны

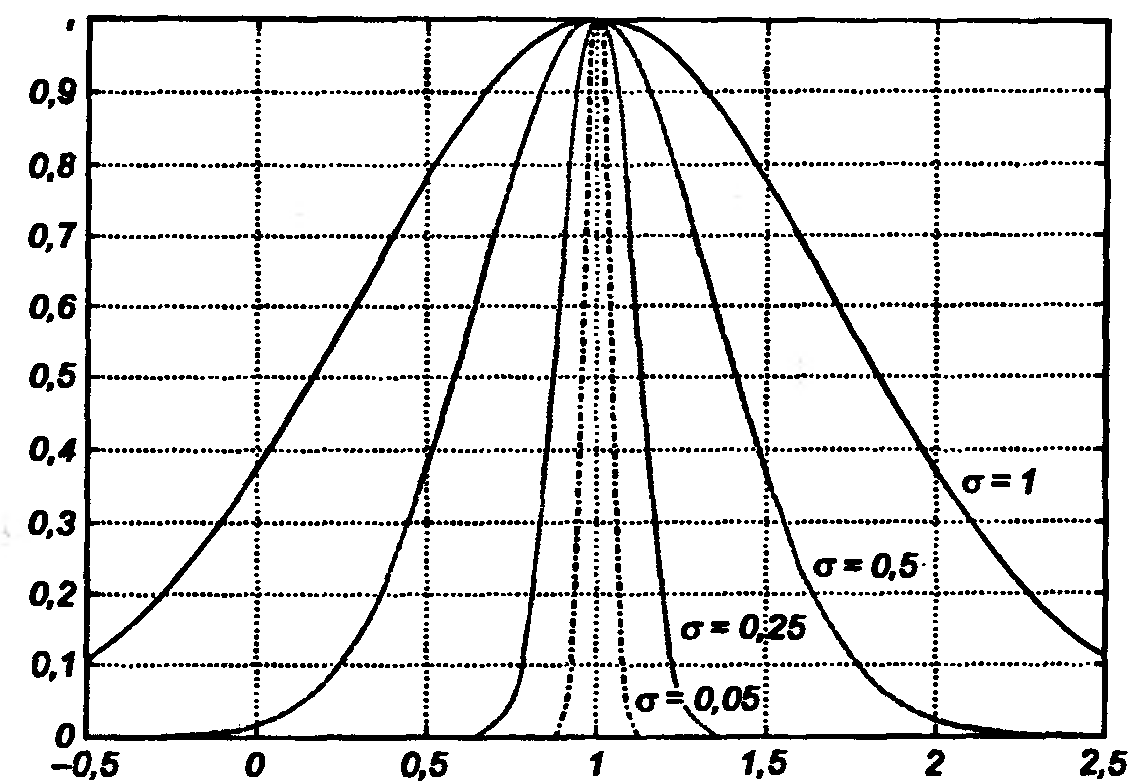
• обобщенная гауссовская функция в экспоненциальном

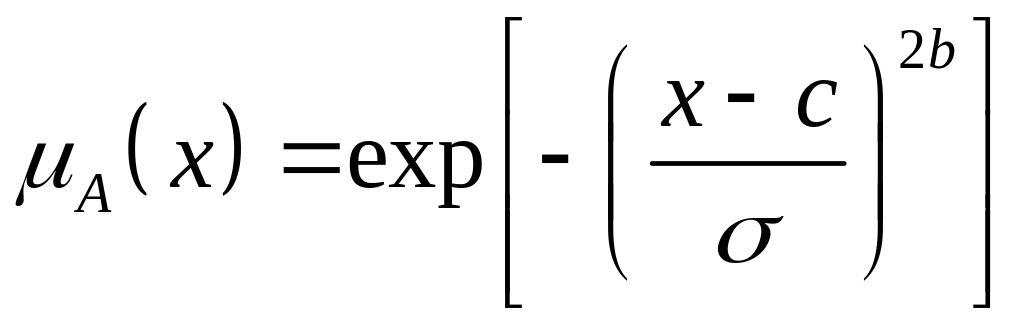(7.7)

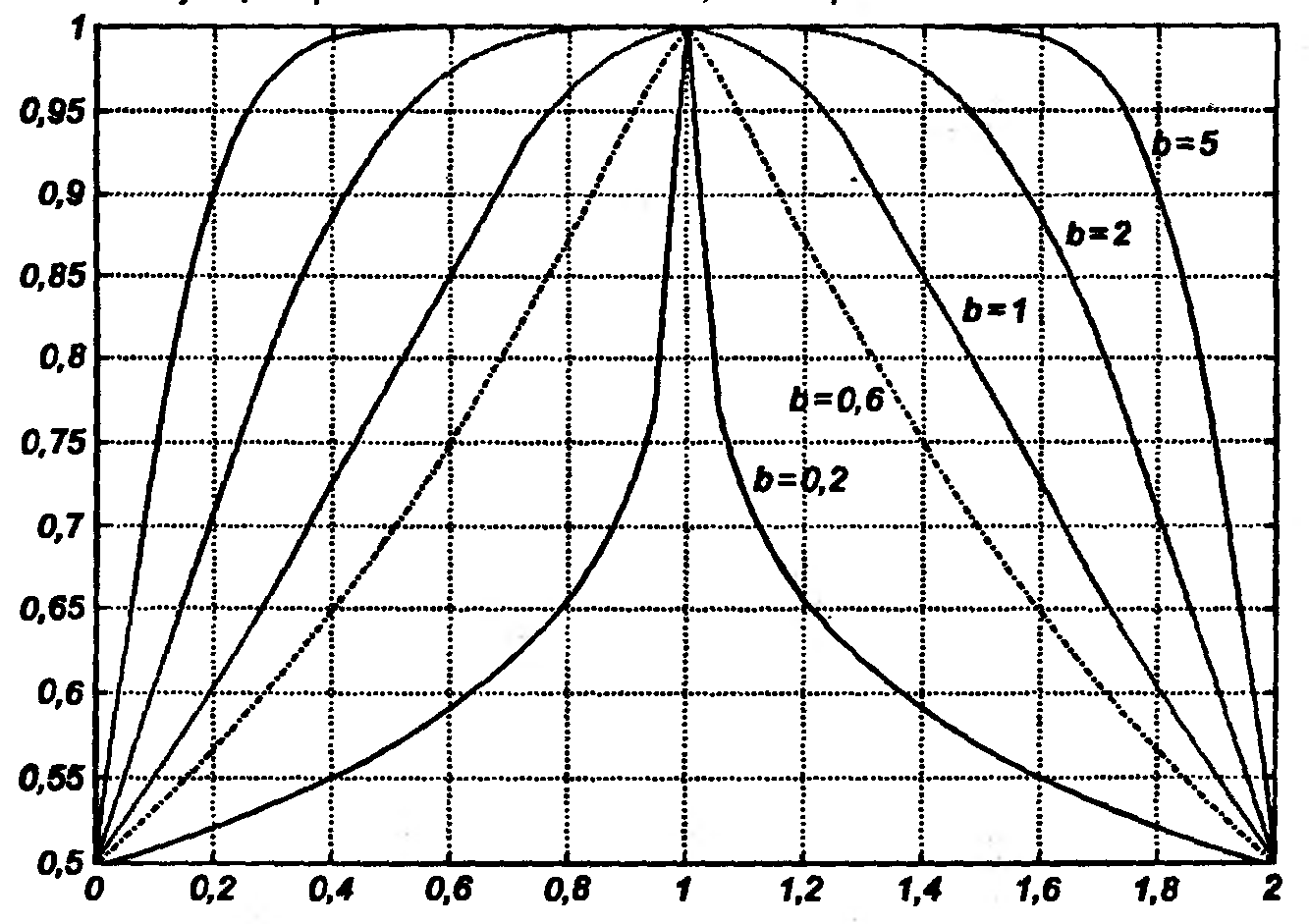
или рациональном 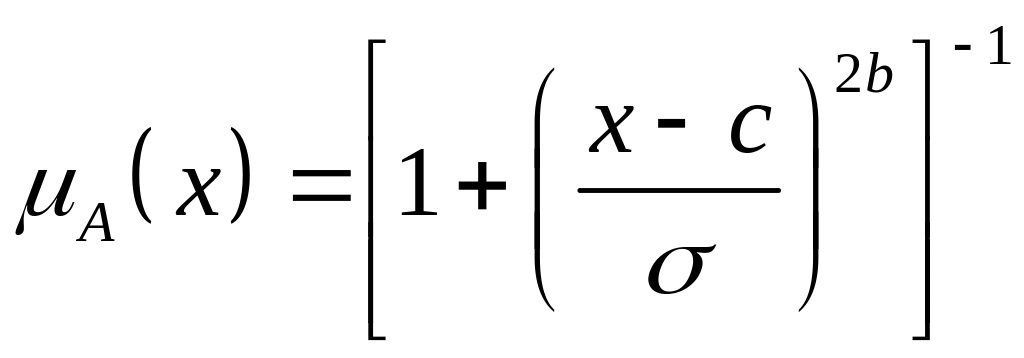(7.8)

виде, зависимость формы которой от значений с, , b показана на рис. 7.3 а, б, в соответственно. Заметим, что при b0,5 гауссова кривая соответствует треугольной, а при b>5 – трапециидальной функциям;

• симметричная треугольная функция (рис. 7.4)

(7.9)

• трапецеидальная функция (рис. 7.5)

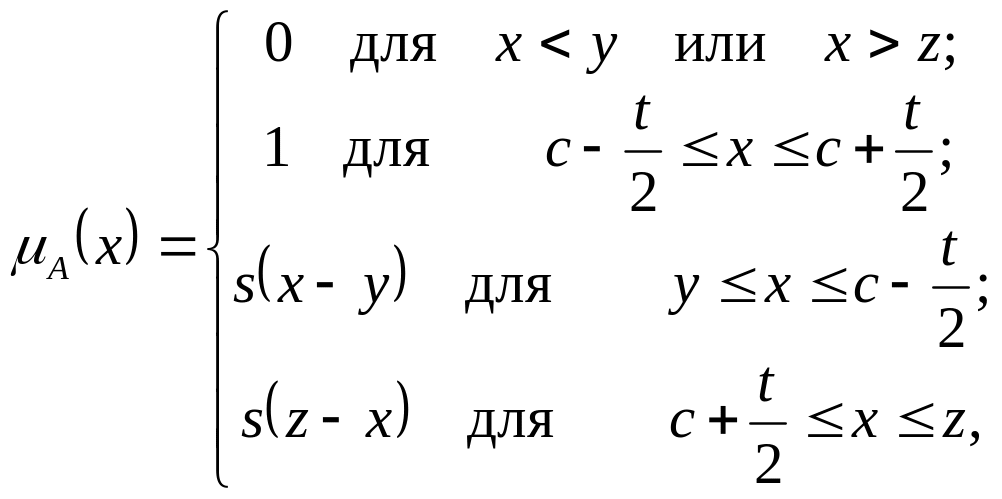(7.10)

где s – угол наклона, с – центр. При t=0 трапецеидальная функция редуцирует до треугольной формы.

а (x) )	б (x) )
х	х
в (x) )
х Рис. 7.3. Влияние параметров обобщенной гауссовской функции на ее форму: а) размещение центра с при =1; b=1; б) значения  при с=1; b=1; в) значения b при с=1; =1

Дефаззификатор трансформирует нечеткое множество с _АВ (х, y)(y) в детерминированное решение y, что можно выполнить различными способами дефаззификации:

– относительно центра области

или ; (7.11)

– относительно среднего центра

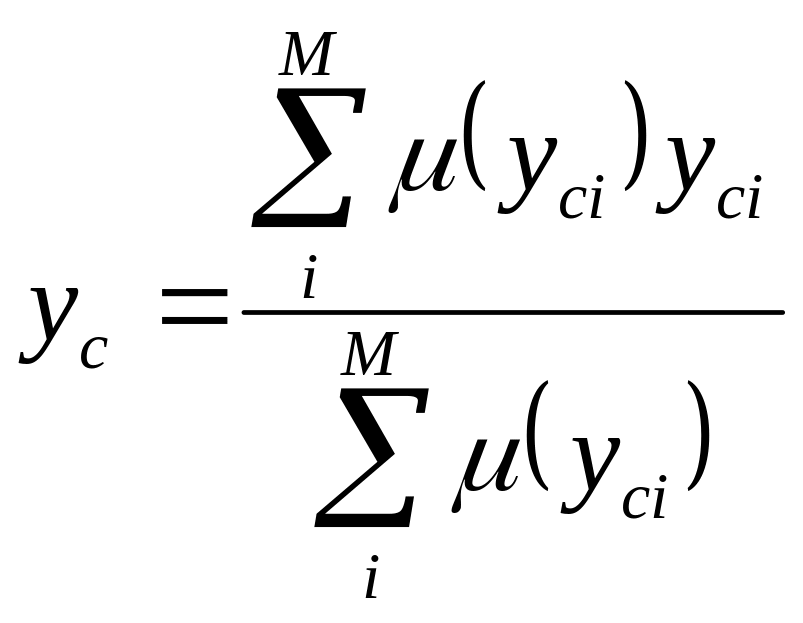, (7.12)

где y_ci – центр i–го нечеткого правила,  (y_ci) – соответствующее значение функции принадлежности;

– относительно среднего максимума

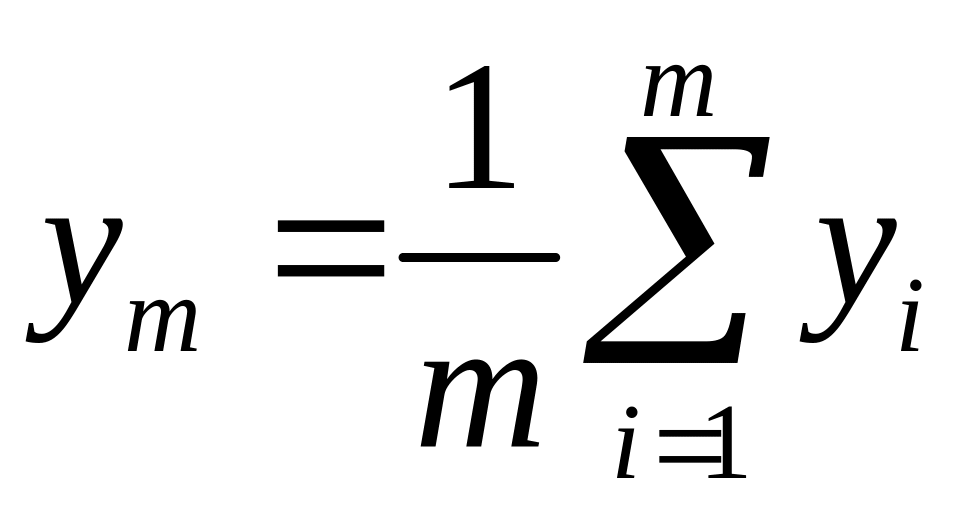, (7.13)

где m – количество точек переменной y, в которых  (y) достигает максимального значения;

– выбором минимального из максимальных значений y

y_s – наименьшее из y, для которых  (y)=max; (7.14)

– выбором максимального из максимальных значений y

y_l – наибольшее из y, для которых  (y)=max. (7.15)

Влияние различных способов дефаззификации на итоговое решение рассмотренного ранее примера (рис. 7.2) приведено на рис. 7.6. На практике чаще всего применяется дефаззификация относительно среднего центра.

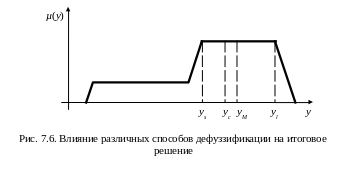
Если в модели Мамдани–Заде в качестве агрегатора использовать оператор алгебраического произведения, то каждое из M правил определит уровень активации условия

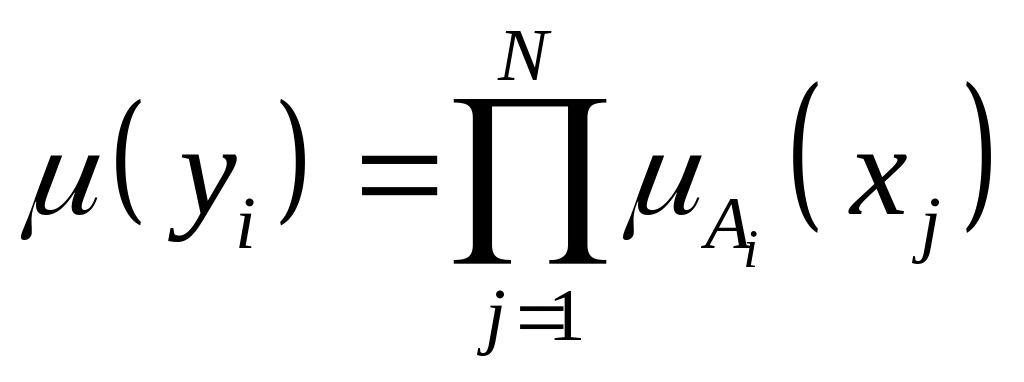, (7.16)

где x_j – компоненты входного вектора , а y_i – значения y, при которых  (y_i ) максимально. Тогда дефаззификация относительно среднего центра дает

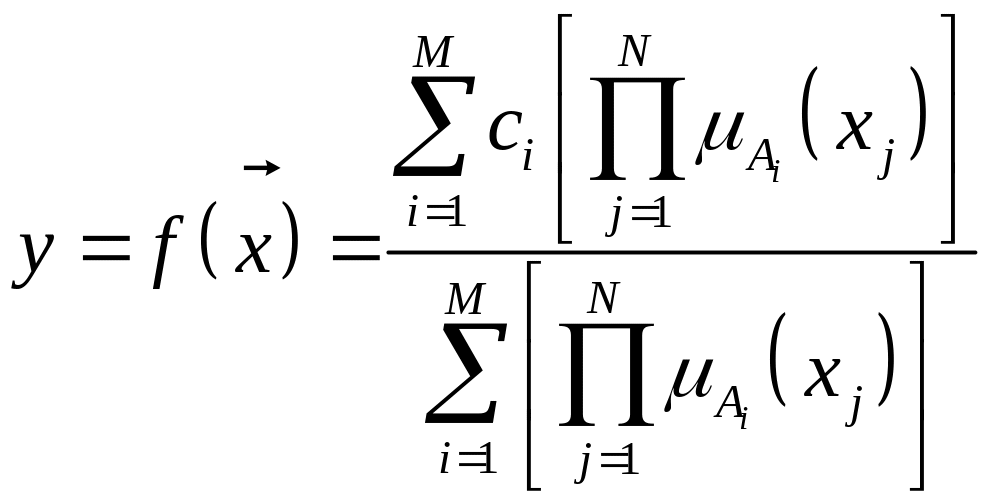, (7.17)

где c_i – центр нечеткого множества заключения i–го правила вывода. При _Ai (x_j ) в виде обобщенной гауссовской функции (7.7) или (7.8) выражение (7.17) определяет непрерывную функцию, которая при соответствующем подборе параметров _Ai (x_j ) и коэффициентов c_i может аппроксимировать любую заданную с произвольной точностью , т.е. модель Мамдани–Заде выступает в качестве универсального аппроксиматора.

Среди нечетких систем адаптивного типа наибольшей популярностью пользуется модель вывода Такаги–Сугено–Канга (TSK), где функция заключения определяется нечетким, но точечным образом, благодаря чему модель значительно упрощается, поскольку дефаззификатор на выходе не требуется. В векторной форме общая модель TSK может быть записана как

если это , то , (7.18)

где – четкая функция, на практике чаще всего в виде полинома 1–го порядка

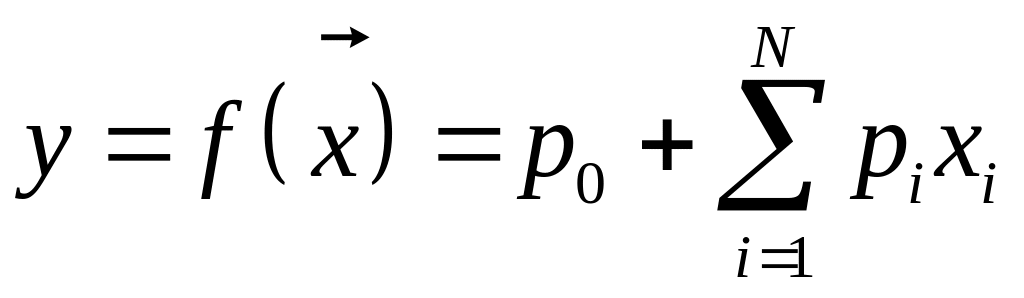, (7.19)

где р₀, р₁, …, р_N – вещественные коэффициенты, подбираемые в процессе адаптации (обучения). Еще более простая модель вывода TSK получается при использовании f(x) в виде полинома нулевого порядка

y = f(x) = p₀ , (7.20)

где p₀ соответствует центру заключения c_i модели Мамдани–Заде (7.17).

Если модель TSK содержит M правил вывода, то выход системы определяется как

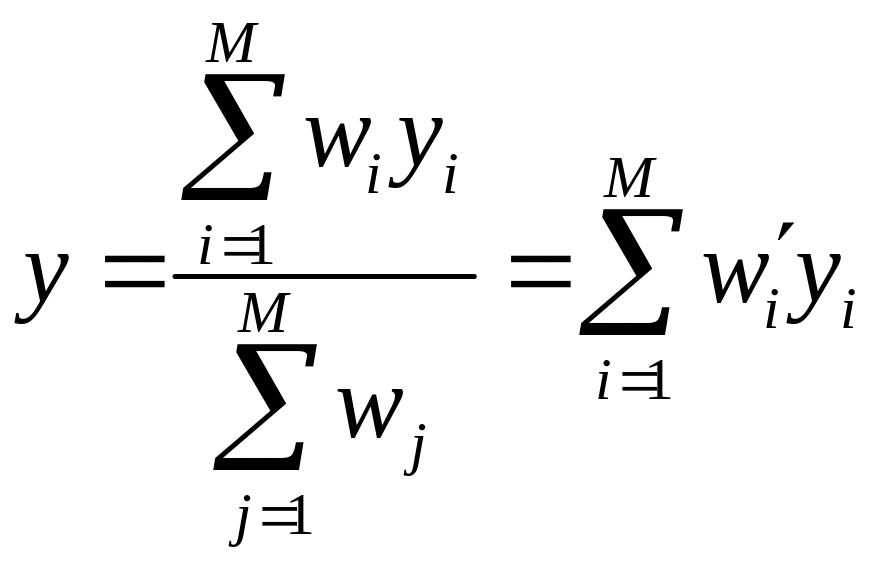, (7.21)

где для каждого i–го правила (i = 1, 2, …, M) реализуется функция TSK 1–го порядка

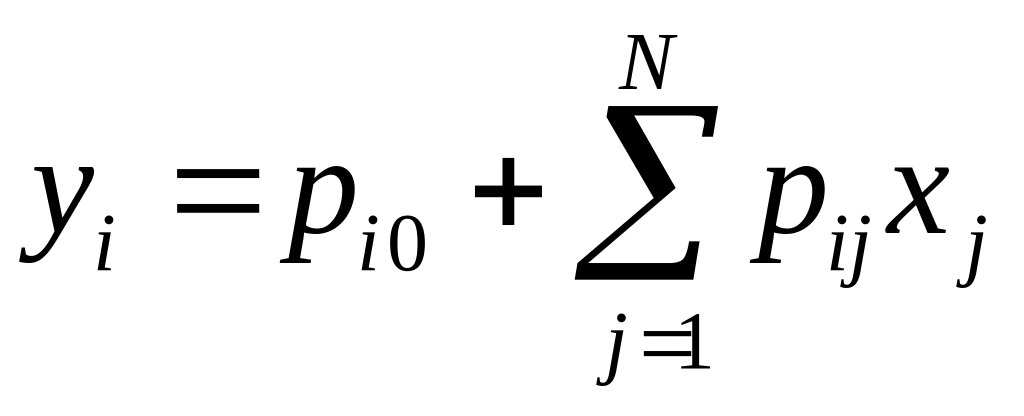, (7.22)

Видно, что выходная функция y линейна относительно всех входных переменных x_j, однако веса w_i являются нелинейными параметрами, значения которых уточняются в процессе обучения как результат агрегирования правил, соответствующих конкретным компонентам .