37

______________________________________________________________________________________________

Приложения производной

4.1. Правило Лопиталя

Часто при вычислении пределов функции вида y=f (x)/g (x) в точке a оказывается, что f (x)=0, g(x)=0. В этом случае говорят, что в точке a имеет место неопределенность типа 0/0. Для раскрытия таких неопределенностей, то есть для вычисления предела  f (x)/g (x), можно применять прием, известный как правило Лопиталя.

Теорема. Пусть функции f (x) и g(x) определены и дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, причем f (x)= g(x)=0,

при этом f (x)/g (x)=A. Тогда f (x)/g (x)=A.

Пример. Вычислим предел (e^3x-1)/sin2x. Поскольку здесь неопределенность 0/0, применим правило Лопиталя: (e^3x-1)/sin2x = 3e^x/(2cos 2x) = 1,5.

4.2. Исследование функций на монотонность и экстремум

4.2.1. Монотонность функции на интервале и условия экстремума.

Теорема. Если функция y=f (x) дифференцируема на интервале (a,b) и в каждой точке этого интервала f’(x)=0, то эта функция является постоянной на интервале (a,b).

Теорема (достаточное условие монотонности на отрезке). Если функция y=f(x) непрерывна на отрезке [a,b] и имеет в каждой точке интервала (a,b) положительную (отрицательную) производную, то она возрастает (убывает) на отрезке [a,b].

Интервалы монотонности функции y=f(x) являются интервалами знакопостоянства ее производной.

Теорема (необходимый признак экстремума). Пусть x_0 ‑ точка экстремума функции. Тогда в этой точке производная равна нулю или не существует.

Определение. Точки, в которых производная равна нулю или не существует, называются критическими.

Рис. 4.2.2

Теорема (первое достаточное условие экстремума). Точка x₀ является точкой экстремума функции y = f(x), непрерывной в точке x₀, если производная f’(x) при переходе через эту точку меняет знак. При этом точка x₀ является точкой максимума, если знак производной меняется с положительного на отрицательный, а при перемене знака с отрицательного на положительный ‑ точкой минимума.

Пример. Эта теорема иллюстрируется на рис. 4.2.2, где изображен график функции, имеющей две точки экстремума. При этом в точке x₂ производная равна нулю, а в точке x₁ ‑ не существует. Для исследования функции на экстремум можно использовать вторую производную.

Теорема (второе достаточное условие экстремума). Если функция y= f (x) дважды дифференцируема в точке x₀ , причем в этой точке первая производная равна нулю, а вторая производная положительна (отрицательна), то в точке x₀ функция достигает локального минимума (максимума).

Рис. 4.2.3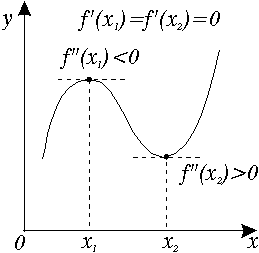

Пример. Эта теорема иллюстрируется на рис. 4.2.3, где изображен график функции такой, что f (x₁)= f (x₂)= 0 и f(x₁)< 0,  f(x₂ )> 0. Поэтому x₁ ‑ точка локального максимума, а x₂ ‑ точка локального минимума этой функции.

Итак, для исследования функции y = f (x) на монотонность и экстремум нужно выполнить следующие действия.

1. Найти первую производную функции f (x).

2. Найти критические точки функции.

3. Определить интервалы монотонности и точки экстремума.

4. Вычислить значения функции в точках экстремума.

Рис.4.2.4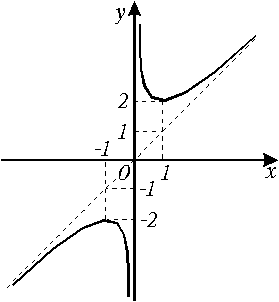

Пример. Исследовать на экстремум и найти интервалы монотонности функции у = х+1/х.

1). Находим производную: у'=1-1/x².

2). Эта производная существует на всей числовой оси, кроме точки x=0, критическими точками являются x=1 и x= -1.

3). При |x| >1 производная положительна, а при |x|<1 ‑ отрицательна. Следовательно на интервалах (-,-1) и (1,+ ) функция возрастает, а на интервалах (-1,0) и (0,1) ‑ убывает. При этом в точке x=-1 функция имеет максимум, а в точке x=1 ‑ минимум.

4). f (-1)=-2, f (1)=2.

Построить самостоятельно график гиперболы у=х+1/х

Найти для этой функции вертикальную и наклонную асимптоты.

Пример. Функция полных издержек (функция затрат, кривая «затраты-выпуск») однопродуктовой фирмы задана уравнением C = Q²+2Q+9. Здесь Q ‑ объем выпуска продукции, C ‑ соответствующие издержки производства. При каком объеме производства средние издержки минимальны?

Решение. Средние издержки AC(Q) равны полным затратам, отнесенным на единицу продукции, то есть в данном случае

AC(Q)=C(Q)/Q =(Q²+2Q +9)/Q = Q +2 + 9/Q.

Графиком функции средних издержек Y = AC(Q) является гипербола с наклонной асимптотой Y=Q+2. При этом минимум функции средних издержек определяется из условия AC'(Q)=0, откуда получаем

(Q +2 + 9/Q)= 1-9/Q² = 0,

вследствие чего минимум средних издержек достигается при Q = 3. То, что Q = 3 является точкой минимума, следует, в частности, из второго достаточного условия экстремума: в этой точке значение второй производной функции средних издержек положительно

(AC'(Q) = = (1-9/Q²)= 18/Q³).

Пример. Функция полных издержек однопродуктовой фирмы задана уравнением C = Q²+2Q+9. Цена p товара на рынке равна 12. Определить область безубыточности. При каком объеме производства фирма получит максимальную прибыль, если весь товар находит покупателя?

Решение. Прибыль I фирмы определяется как разность между доходом (выручкой от продажи) и полными издержками:

I(Q) = R(Q) - C(Q).

Поскольку цена продукции постоянна, то R = pQ = 12Q, вследствие чего графиком функции прибыли является парабола, ветви которой направлены вниз:

I(Q) = 12Q - (Q²+2Q + 9) = 10Q-Q²-9.

Область безубыточности определяется из решения неравенства 10Q-Q²-9 ≥ 0. Так как корнями квадратного трехчлена, стоящего в левой части неравенства, являются числа Q₁=1 и Q₂=9, то областью безубыточности является интервал (1,9). Итак, при 1 < Q < 9 прибыль фирмы положительна. Найдем теперь значение объема выпуска продукции, при котором прибыль достигает своего максимального значения. Из необходимого условия экстремума I' (Q) = 0 получаем 10 = 2Q, т.е. Q_max =5.

Пример. Функция полных издержек однопродуктовой фирмы задана уравнением C = Q²+2Q+9. Цена p товара на рынке равна 12. Определить область безубыточности, если с каждой единицы товара фирма выплачивает в бюджет налог в размере t. Определить, при каком наибольшем целом значении налоговой ставки производство продукции может быть прибыльным.

Решение. Прибыль фирмы после налогообложения I_t определяется как разность между доходом (выручкой от продажи), полными издержками и отчислениями в бюджет:

I_t (Q) = pQ - C(Q) - tQ.

Графиком функции прибыли, как и в предыдущей задаче, является парабола, ветви которой направлены вниз:

I_t(Q) = (10 - t )Q-Q²-9 = -(Q-Q₁)(Q-Q₂).

Здесь Q_1,2=(10-t ((4-t)(16-t))^1/2)/2 ‑ корни квадратного трехчлена. Поэтому теперь область безубыточности (Q₁,Q₂) зависит от значения параметра t. Заметим, что при t = 0 из полученных формул следует Q₁=1, Q₂= 9. Если ставки налога начинает увеличиваться , то Q₁ тоже начинает расти, а Q₂ – уменьшается. Более того, интервал (Q₁,Q₂) лежит в положительной области лишь при значениях налоговой ставки 0  t < 4. При t = 4 функции прибыли после налогообложения имеет вид

I_t(Q) = (10 - t )Q-Q²-9 = - (Q-3)²  0.

Поэтому наибольшее целое значение налоговой ставки, при котором производство продукции является прибыльным, равно t = 3. В этом случае максимум прибыли достигается при Q_max= (10-3)/2=3,5; выручка от продажи равна pQ_max= 42; издержки производства составляют C(Q) = 30,25; отчисления в бюджет равны tQ=10,5. Поэтому прибыль после налогообложения составит I_t = 42-30,25-10,5= 1,25. Как видим, отчисления в бюджет при налоговой ставке t = 3 более чем в 8 раз превышают прибыль фирмы после налогообложения.