
- •§1. Системы любых уравнений: определения, геометрическая трактовка, равносильность, основные методы решения
- •§2. Некоторые приёмы решения систем нелинейных уравнений
- •1. Исключение одной неизвестной в простейшем случае, когда в системе есть линейное уравнение
- •2. Преобразование системы с целью получить линейное уравнение.
- •3. Введение вспомогательной неизвестной (частичная замена неизвестных)
- •4. Полная замена неизвестных
- •5. Симметричные системы
- •6. Использование однородного уравнения в системе
- •7. Графическое решение систем с целью определения количества решений
§1. Системы любых уравнений: определения, геометрическая трактовка, равносильность, основные методы решения
Системой называется любое конечное множество уравнений. В общем случае можно рассматривать системы m уравнений относительно n неизвестных. Причём, возможны все три случая:
1)
![]() – система называется замкнутой;
– система называется замкнутой;
2)
![]() – система называется незамкнутой,
или недоопределённой;
– система называется незамкнутой,
или недоопределённой;
3)
![]() – система называется переопределённой.
– система называется переопределённой.
Решением системы уравнений с n неизвестными называется упорядоченный набор из n чисел, удовлетворяющих каждому уравнению системы.
Решить систему – это значит найти все её решения или доказать отсутствие решений.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
ПРИМЕРЫ
Охарактеризуем следующие системы:
1)

![]()
![]() является решением системы, следовательно,
система является переопределённой и
совместной;
является решением системы, следовательно,
система является переопределённой и
совместной;
2)

система не имеет решений, следовательно, система является переопределённой и несовместной.
Вывод 1. Переопределённая система чаще всего (но не всегда!) бывает несовместной.
3)

система
имеет два решения:
![]() и
и
![]() , следовательно, система является
замкнутой и совместной.
, следовательно, система является
замкнутой и совместной.
Вывод 2. Система, в которой число уравнений совпадает с числом неизвестных, чаще всего (но не всегда!) является совместной и имеет конечное множество решений.
4)

система является недоопределённой и совместной, имеет бесконечное множество решений.
Вывод 3. Недоопределённая (незамкнутая) система чаще всего бывает совместной и имеет бесконечное множество решений.
Геометрическая трактовка уравнений и систем с двумя неизвестными
|
Одно уравнение
|
|
Система двух уравнений:
|
|
Система трёх уравнений:
Если такая переопределённая система
имеет решение
|
ПРИМЕРЫ
1. Определим количество решений системы, построив графики её уравнений:
1) |
2)
|
3)
|
|
|
|
4)
|
||
2. Определим значения параметра k, при которых будет совместной каждая из следующих систем:
1)
|
2)
|
Ответ: только
при
|
Ответ: только при . |
Равносильность систем
Две системы называются равносильными на некотором числовом множестве, если они имеют совпадающие наборы решений на этом множестве.
ПРИМЕРЫ
1. Установим, на каком множестве равносильны следующие пары систем:
1)
![]() и
и

2-я система:

системы
равносильны на множестве
![]() пар
пар
![]() действительных чисел;
действительных чисел;
2)
![]() и
и

системы равносильны на множестве
пар
действительных чисел, из которого
удалена пара
![]() .
.
2. Сделав равносильные переходы для
системы
 ,
найдём все её решения:
,
найдём все её решения:

 .
.
Таким образом, система имеет два решения
![]() .
.
Перечислим основные действия над системами, которые гарантированно приводят к системе, равносильной данной:
1. Любое уравнение системы заменить на ему равносильное уравнение.
2. Одно уравнение системы заменить почленной суммой, разностью, произведением или отношением двух уравнений системы.
3. Если в системе одна неизвестная выражена через другие, то можно осуществить подстановку этого выражения во все уравнения системы:
 .
.
4. Если система содержит уравнение, в
котором левая часть представлена
произведением нескольких выражений, а
правая часть равна нулю, то есть уравнение
вида
![]() ,
,
то она равносильна совокупности нескольких систем:
 .
.
5. Если система содержит неизвестные под знаком модуля, то она равносильна совокупности нескольких систем с условиями, при которых раскрываются модули.
Например,
 .
.
Основные методы решения любых систем
Метод исключения неизвестных, который осуществляется способом подстановки или способом алгебраического сложения уравнений.
Метод замены неизвестных.
Графический метод.
УПРАЖНЕНИЯ
Задача 1
Решите систему, выполнив равносильные переходы от заданной системы к значениям неизвестных:
1)
 2)
2)

3)
 4)
4)

Ответы: 1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]()
![]() .
.
.
Задача 2
Определите графически, сколько решений имеет каждая из следующих систем.
1)
 2)
2)
 3)
3)
 4)
4)

Ответы: 1) 2 решения; 2) 3 решения; 3) 4 решения; 4) 0 решений.
Задача 3
Определите, при каком значении параметра с каждая из следующих систем будет совместной:
1)
 2)
2)
 3)
3)
 4)
4)

Ответы: 1) при
![]() ; 2)
при
; 2)
при
![]() и
при
и
при
![]() ;
;
3) при
![]() ;
4) при
;
4) при
![]() .
.
Задача 4
Решите следующие системы:
1)
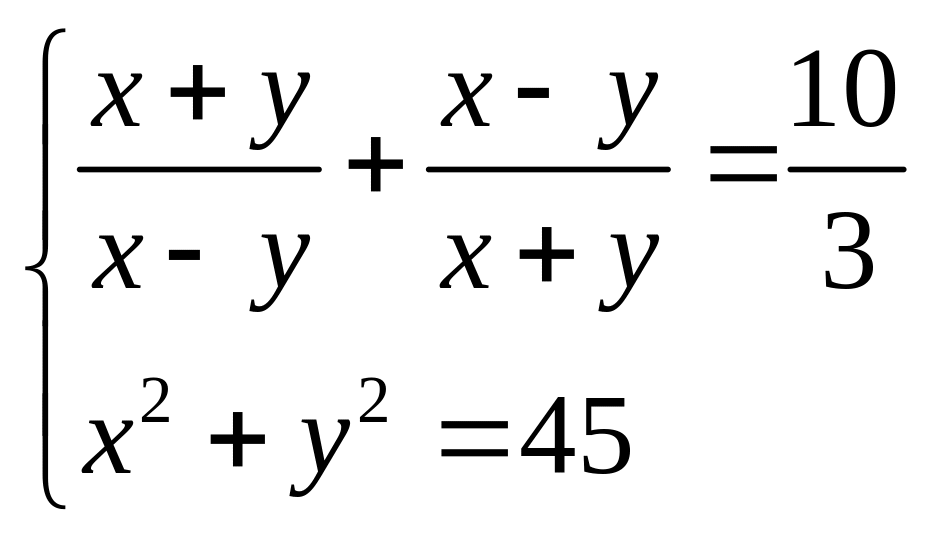 2)
2)
 3)
3)

4)
 5)
5)
 6)
6)
 .
.
Ответы: 1)
![]() ;
2)
;
2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ;
6)
;
6)
![]() .
.
Задача 5
Определите количество решений системы в зависимости от параметра а:
1)
 2)
2)
 3)
3)
 4)
4)

Ответы:
1) |
|
0, если
2, если
4, если
|
2) |
|
0 при
4 при
8 при
|
4) |
4) |
|
0, если
1, если
2, если
|
3) |
|
0 при
1 при
2 при
|




 .
.
 – 2 решения;
– 2 решения;  – 0 решений;
– 0 решений;






