
- •П.1 Логарифмічна функція і її властивості …………………………………
- •Розділ 1. Вступні зауваження і факти
- •§1. Комплексні числа. Операції над комплексними числами
- •§2. Збіжність послідовностей комплексних чисел
- •§3 Нескінченно віддалена точка. Розширена комплексна площина. Стереографічна проекція
- •§4 Ряди комплексних чисел
- •§5 Комплекснозначні функції комплексного аргументу та деякі їх властивості
- •Розділ 2. Похідна функції комплексного аргументу. Аналітичні функції
- •§1 Похідна функції комплексної змінної. Критерій її існування
- •Доведення
- •§2 Геометричний зміст аргументу і модуля похідної
- •§3 Дробово-лінійна функція. Властивості і відображення здійснювані нею
- •П.1 Група дробово-лінійних відображень
- •П.2. Кругова властивість дробово-лінійних відображень
- •П.3. Нерухомі точки дробово-лінійного відображення
- •§4 Експоненціальна і тригонометрична функції в комплексній області
- •П.1 Логарифмічна функція і її властивості
- •§5 Виділення однозначних віток многозначної функції
- •§6 Показникова та степенева функції в комплексній області
Зміст
Розділ 1. Вступні зауваження і факти
§1. Комплексні числа. Операції над комплексними числами ...........................
§2. Збіжність послідовностей комплексних чисел .............................................
§3. Нескінченно віддалена точка. Розширена комплексна площина. Стереографічна проекція ................................................................................
§4. Ряди комплексних чисел .................................................................................
§5. Комплекснозначні функції комплексного аргументу та деякі їх властивості ..............................................................................................................
Розділ 2. Похідна функції комплексного аргументу. Аналітичні функції
§1. Похідна функції комплексної змінної. Критерій її існування .....................
§2. Геометричний зміст аргументу і модуля похідної .......................................
§3. Дробово-лінійна функція. Властивості і відображення здійснювані нею
П.1 Група дробово-лінійних відображень ......................................................
П.2. Кругова властивість дробово-лінійних відображень .............................
П.3. Нерухомі точки дробово-лінійного відображення .................................
§4. Експоненціальна і тригонометрична функції в комплексній області ........
П.1 Логарифмічна функція і її властивості …………………………………
§5. Виділення однозначних віток многозначної функції .................................
§6. Показникова та степенева функції в комплексній області .........................
Розділ 1. Вступні зауваження і факти
§1. Комплексні числа. Операції над комплексними числами
Нагадаємо
далі деякі відомості про комплексні
числа.
Число
виду
![]() ,
де
,
де
![]() ,
та
,
та
![]() називається комплексним числом. Таку
форму запису комплексного числа
називають алгебраїчною.
називається комплексним числом. Таку
форму запису комплексного числа
називають алгебраїчною.
![]() − дійсна частина;
− дійсна частина;
![]() −
коефіцієнт при
уявній частині.
−
коефіцієнт при
уявній частині.
Очевидно,
що між множиною
![]() комплексних чисел і точками простору
комплексних чисел і точками простору
![]() є взаємно однозначна відповідність.
є взаємно однозначна відповідність.
![]()
![]()
![]() .
.
Множина
дійсних чисел
![]() є підмножиною множини
комплексних чисел. Кажуть, що множина
є розширенням множини
.
Число
є підмножиною множини
комплексних чисел. Кажуть, що множина
є розширенням множини
.
Число
![]() називають уявною
одиницею.
називають уявною
одиницею.
На множині операції додавання і множення визначаються наступним чином
![]() ,
,
![]() .
.
О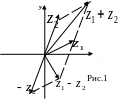 перації
віднімання і ділення одержуємо за
алгебраїчним принципом, якщо врахувати,
що нульовим елементом тут є число
перації
віднімання і ділення одержуємо за
алгебраїчним принципом, якщо врахувати,
що нульовим елементом тут є число
![]() ,
одиничним −
,
одиничним −
![]() ,
протилежним до числа
,
протилежним до числа
![]() є число
є число
![]() ,
симетричним (оберненим) (якщо
,
симетричним (оберненим) (якщо
![]() )
до цього числа є число
)
до цього числа є число
![]() :
:
![]() ,
,
![]() .
.
Геометричну інтерпретацію додавання і віднімання комплексних чисел див. на рис. 1.
Неважко переконатися, що відносно операцій додавання і множення комплексні числа утворюють поле.
Поряд
з комплексним числом
розглядають спряжене
комплексне
число
![]() .
Звідси маємо, що справедливі рівності
.
Звідси маємо, що справедливі рівності
![]() ,
,
![]() ,
,
![]() .
.
причому
![]() ,
,
Комплексні
числа можна записувати
не тільки в алгебраїчній формі, а й в
так званій
тригонометричній
формі. Візьмемо комплексне число
![]() ,
яке зображене на рис. 2. Довжина вектора
,
яке зображене на рис. 2. Довжина вектора
![]() називається модулем
числа
називається модулем
числа
![]() (позначається
(позначається
![]() ),
а кут φ, який утворює вектор
з додатним напрямом осі
),
а кут φ, який утворює вектор
з додатним напрямом осі
![]() ,
називається аргументом
комплексного числа
і позначається
,
називається аргументом
комплексного числа
і позначається
![]() .
З рисунка видно, що
.
З рисунка видно, що
![]() .
.
Т ака
форма запису комплексного числа
називається тригонометричною.
Очевидно, що справедливі наступні
рівності
ака
форма запису комплексного числа
називається тригонометричною.
Очевидно, що справедливі наступні
рівності
![]() ,
,
![]() .
.
Оскільки
аргумент будь-якого комплексного числа
(за винятком 0, для якого аргумент
невизначений), набирає безліч значень,
то домовимось те значення аргументу
,
яке попадає на
![]() називати головним значенням аргументу
і позначати
називати головним значенням аргументу
і позначати
![]() .
Тоді зрозуміло, що кожне відмінне від
0 комплексне число має свій єдиний модуль
і своє єдине головне значення аргументу.
.
Тоді зрозуміло, що кожне відмінне від
0 комплексне число має свій єдиний модуль
і своє єдине головне значення аргументу.
Подивимося
як перемножити два комплексні числа,
записані в тригонометричній формі.
Нехай маємо числа
![]() і
і
![]() .
Тоді добуток двох комплексних чисел
.
Тоді добуток двох комплексних чисел
![]() і
і
![]() буде
записуватися за формулою
буде
записуватися за формулою
![]() ,
,
 яку
можна отримати, записавши добуток
комплексних чисел в алгебраїчній формі.
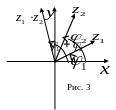
Геометричний зміст добутку комплексних
чисел, записаних в тригонометричній
формі, видно з рис. 3.
яку
можна отримати, записавши добуток
комплексних чисел в алгебраїчній формі.
Геометричний зміст добутку комплексних
чисел, записаних в тригонометричній
формі, видно з рис. 3.
Легко здогадатися, що
![]() .
.
З правила множення комплексних чисел, записаних в тригонометричній формі, одержуємо формулу піднесення комплексного числа до натурального степеня:
![]() .
.
Вище записана формулу називають формулою Муавра.
З'ясуємо
тепер як добувати корінь n-го
степеня з комплексного числа. Нехай
маємо комплексне число
![]() .
Тоді
.
Тоді
![]() |
|
![]() .
Нехай
.
Нехай
![]() ,
де
,
де
![]() і
і
![]() − невідомі. Для знаходження
і
скористаємось тим, що
і
формулою Муавра. Одержимо:
− невідомі. Для знаходження
і
скористаємось тим, що
і
формулою Муавра. Одержимо:
![]() .
.
З останньої рівності маємо:
![]() і
і
![]() ,
,
![]()
![]()
![]() і
і
![]() ,
.
,
.
Отже,
![]() ,
.
,
.
Різні
значення в дужках одержимо лише при
k=0,
1, 2,..., n-1.
Якщо k
надаватимемо інших значень, то в дужках
одержимо одне із раніше отриманих чисел.
Таким чином остання формула дає значення
кореня n-го
степеня з комплексного числа і попередній
аналіз показує, що цей корінь
n-значний
(якщо
).
Якщо ми зобразимо всі значення кореня
n-го
степеня з комплексного числа
на комплексній площині, то вони лежатимуть
у вершинах правильного n-кутника,
вписаного в коло радіуса
![]() .
.
Зауважимо, що із раніше сказаного маємо
![]() ,
,
![]() ,
,
 ,
,
![]() .
.
Можна довести, що тут теж мають місце нерівності, відомі нам з дійсного аналізу
![]() ,
,
![]() .
.
