44

Г.М. Ильмушкин

ВЫСШАЯ МАТЕМАТИКА В УПРАЖНЕНИЯХ И ЗАДАЧАХ

для студентов заочного обучения технологических

специальностей

Глава III. Теория вероятностей

3.1. Основные понятия

1. Алгебра событий

Произвольное множество будем называть пространством элементарных событий. Элементы этого множества назовем элементарными событиями. Эти понятия являются первоначальными. В реальном опыте элементы интерпретируются как взаимно исключающие исходы изучаемого случайного явления. Для описания каждой реальной задачи множество выбирается наиболее подходящим образом. Приведем ряд примеров поясняющих выбор множества .

1. Пусть монета подбрасывается один раз. При бросании монеты возможны исходы: выпадение герба, выпадение “Решетки“. Итак, при описании этого опыта мы полагаем ={ }, где соответственно означают выпадение герба и выпадение решетки.

2. Теперь рассмотрим подбрасывание игральной кости, т.е., однородного кубика, на каждой грани которого написано различное число от 1 до 6. Естественно в этом случае следует выбрать ={ }, где (к=1,2,…,6) означают исход опыта, заключающийся в выпадении к очков. Имеем шесть исключающих друг друга исходов.

3. Далее рассмотрим подбрасывание монеты n раз. Каждому исходу опыта поставим в соответствие последовательность из n чисел последующему правилу: если при к- ом подбрасывании монеты выпал герб, то на к-ом месте последовательности фиксируем Г, а при выпадении решетки –Р. Например, последовательность (РР…РР) означает исход опыта, заключающийся в том, что каждый раз выпала решетка при n испытаниях. В частности, при n =3 принимаем ={ГГГ, ГГР, ГРГ, ГГГ, РРГ, РГР, ГРР, РРР}. При n больших значениях, число элементарных событий резко возрастает, оно равно .

4. Введем прямоугольную систему координат XOY. Пусть стрелок попадает непременно в какую-либо точку из круга радиуса 10 ед. с центром в начале координат. Тогда есть множество всех точек М(x,y) замкнутого этого круга.

Или можно записать в координатной форме так

.

Однако в реальном опыте кроме взаимоисключающих исходов можно указать много других случайных событий. Например, при бросании игральной кости можно говорить о выпадении четного числа очков. Это событие происходит только в том случае, когда происходит одно из трех элементарных событий

. Представляется естественным каждое реальное событие в математической модели рассматривать как некоторое подмножество А множества .

В дальнейшем будет означать объединение двух множеств А и В, - пересечение этих множеств. Запись означает дополнение А к множеству В, т.е., оно состоит из элементов множества А, не принадлежащих В.

Итак, пусть - произвольное множество, а F – некоторый класс подмножеств множества . F называется алгеброй, если выполняются условия:

1. ;

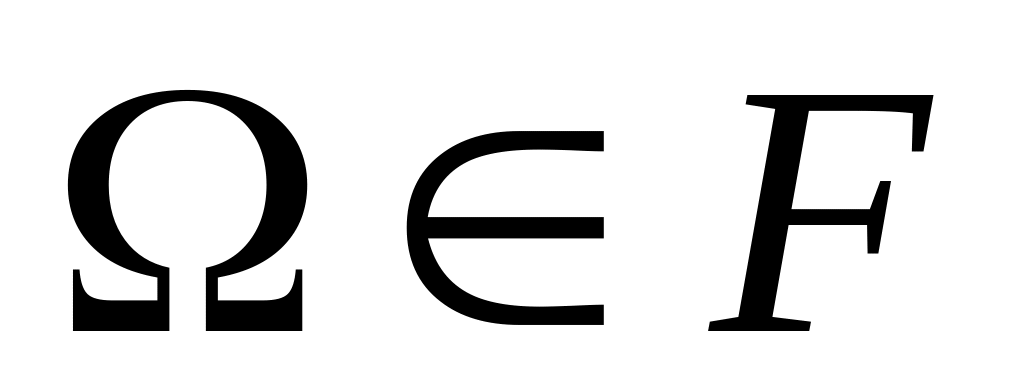1. Для любых : ;

2. Если .

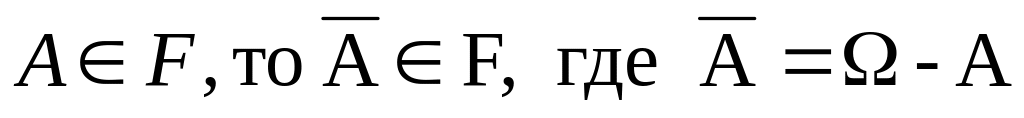Из последнего свойства следует, что .

Замечание 1. Нетрудно заметить, что в условии 2 достаточно требовать выполнения лишь одного из приведенных двух соотношений. Второе будет выполняться автоматически.

Замечание 2. Если -конечное множество, то система всех подмножеств будет также конечным множеством. Если множество состоит из n элементов, то число всех подмножеств равно .

Множество F называется -алгеброй или борелевской алгеброй, если из того, что следует .

Замечание 3. Достаточно выполнялось лишь одно из этих двух соотношений. Второе будет следствием равенства .

Элементы множества F будем называть событиями. Такой подход к понятию события удобен еще и тем , что благодаря ему понятия суммы и произведения событий, а также противоположного события приобретают естественный теоретико-множественный смысл. А именно, под суммой А+В событий А и В будем понимать объединение соответствующих подмножеств, под произведением АВ событий: A и B - пересечение тех же подмножеств, а под противоположным событием понимается событие, соответствующее подмножеству , то есть, дополнение к подмножеству А в .