5.6. Вычисление средних значений физических величин.

Расчет средних значений физических величин имеет важное значение в микромире. Когда в рассматриваемом состоянии квантовомеханической системы физическая величина не имеет определенного значения, т.е. при измерении этой физической величины получается неоднозначный результат, то среднее значение этой величины в какой-то мере характеризует состояние.

Получим формулу для расчета среднего значения величины А, изображающейся эрмитовым оператором Â, в состоянии Ψ. Ради простоты рассмотрим случай дискретного спектра собственных значений оператора: а₁, а₂,…, а_n,… . Если W_n – вероятности обнаружения дозволенных значений а_n (5 постулат) равны | ( φ_n ,Ψ ) | , то по теореме о среднем из теории вероятности:

(5.9)

Учитывая свойства скалярных произведений векторов гильбертова пространства (4.7) и (4.10), получим

Таким образом, для расчета среднего значения физической величины А, изображающейся соответствующим оператором Â, необходимо знать вектор состояния :

(5.10)

Очевидно, если Ψ = φ_n , где φ_n определяется уравнением Âφ_n = a_nφ_n , то формула (5.10) дает следующий результат:

(5.11)

Если ( Ψ,Ψ ) ≠ 1, тогда для среднего значения физической величины справедливо выражение:

(5.12)

5.7. Принцип тождественности (неразличимости) одинаковых частиц.

При изучении свойств систем одинаковых частиц (одного сорта) используется шестой постулат (аксиома), согласно которому в системе одинаковых частиц реализуются лишь такие состояния, которые не меняются при обмене одинаковых частиц.

Этот принцип связан с симметрией волновых функций систем одинаковых частиц, он объясняет существование обменного взаимодействия.

Глава 3. Основы теории представлений

§6. Координатное представление

И в квантовой механике существуют физические величины, обладающие непрерывным спектром собственных значений. Примером таких величин являются координаты частицы x, y, z .

6.1. Векторы состояния в координатном представлении

Рассмотрим ради простоты одномерный случай: частица движется вдоль оси Ox .

Собственные векторы эрмитова оператора координаты являются базисными в координатном представлении. Обозначив их через , запишем уравнение для собственных векторов и собственных значений оператора :

(6.1)

Аналогично, собственный вектор , принадлежащий конкретному значению координаты , удовлетворяет уравнению:

(6.2)

Любой вектор  гильбертова пространства, определяющий состояние одномерной квантовой системы, может быть разложен в интеграл Фурье по базисным векторам согласно формуле:

(6.3)

где коэффициенты разложения записываются в виде:

(6.4)

и представляют собою координаты вектора или его проекции на базисные векторы в координатном представлении.

Вектор обладает единичной нормой , причем норму вектора  можно представить следующим выражением:

.

Этому условию можно удовлетворить, если считать, что собственные векторы оператора с непрерывным спектром собственных значений нормируются на -функцию Дирака:

(6.5)

Тогда

(6.6)

т.е. в координатном представлении проекциями вектора  являются значения комплексной функции при различных значениях , и что - вероятность обнаружения частицы с координатой из интервала . Следовательно, квадраты модулей коэффициентов Фурье-разложения (6.4) представляют известную формулу плотности вероятности .

Таким образом, совокупность проекций или координат –вектора определяет этот вектор  в координатном представлении. Другими словами, множество проекций (координат) называют вектором состояния в координатном представлении или коротко волновой функцией.

Формула (6.5) свидетельствует об ортогональности собственных векторов эрмитова оператора :

, (6.7)

в то же время норма собственных векторов равна ∞.¹

Определим скалярное произведение двух векторов  и  гильбертова пространства в координатном представлении. Записывая векторы  и  в форме разложения по базисным векторам в координатном представлении

получим

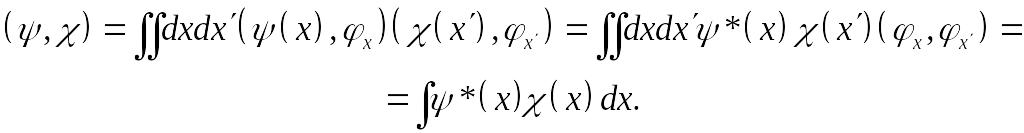(6.8)

Эта формула является обобщением выражения скалярного произведения геометрических векторов на случай векторов гильбертова пространства.