
- •Взаимное расположение прямых.
- •Признаки параллельности двух прямых.
- •Треугольник: определение и виды.
- •Равные треугольники (определение). Признаки равенства треугольников.
- •Равнобедренный треугольник. Признак равнобедренного треугольника (доказательство).
- •Теорема о сумме углов треугольника (доказательство). (стр. 70)
- •Прямоугольный треугольник. Определение и свойства.
- •Теорема Фалеса (доказательство).
- •Подобные треугольники (определение). Признаки подобия треугольников.
Равнобедренный треугольник. Признак равнобедренного треугольника (доказательство).
Если в треугольники два углы равны, то этот треугольник равнобедренный.
Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
Теорема о сумме углов треугольника (доказательство). (стр. 70)
Сумма углов ∆ = 180°.
Доказательство: Проведём через вершину В треугольника АВС прямую а, параллельную АС. ∠1 и ∠4 – накрест лежащие углы при прямых а и АС и секущей АВ. ∠3 и ∠5 – накрест лежащие углы при пересечении тех же прямых секущей ВС. Поэтому ∠1=∠4, ∠5=∠3. Сумма углов 2,4 и 5 = 180° (развёрнутому углу с вершиной В). Отсюда, учитывая равенства ∠1=∠4, ∠5=∠3, получаем: ∠1+∠2+∠3=180°. Теорема доказана.
Теорема о соотношении между сторонами треугольника (неравенство треугольника) (стр. 74).
Неравенство треугольника – каждая сторона треугольника меньше суммы двух других сторон.
Прямоугольный треугольник. Определение и свойства.
Прямоугольный треугольник - ∆, в котором один из углов равен 90° (является прямым).
Катеты – стороны прямоугольного ∆, образующие угол в 90°.
Гипотенуза – самая длинная сторона прямоугольного ∆, лежащая против угла в 90°.
Свойства:
1) сумма острых углов равна 90°;
2) против угла в 30° лежит катет, равный половине гипотенузы;
3) центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы;
4) медиана = половине гипотенузы.
Теорема Пифагора (доказательство). (стр. 130)
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
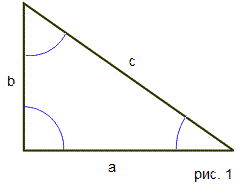
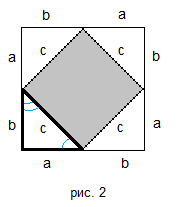
Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c (рис. 1). Докажем, что c2 = a2 + b2. Достроим треугольник до квадрата со стороной a + b так, как показано на рисунке 2. Площадь S этого квадрата равна (a + b)2. C другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна 1/2 ab, и квадрата со стороной c, поэтому S = 4 · 1/2 · ab + c2 = 2ab + с2. Таким образом, (a + b)2 = 2 ab + с2, откуда с2 = a2 + b2. Теорема доказана.
Признаки равенства прямоугольных треугольников. (стр. 77)
1) Если катеты одного прямоугольного ∆ соответственно равны катетам другого прямоугольного ∆, то такие треугольники равны.
2) Если катет и прилежащий к нему острый угол одного прямоугольного ∆ соответственно равны катету и прилежащему к нему острому углу другого прямоугольного ∆, то такие треугольники равны.
3) Если гипотенуза и острый угол одного прямоугольного ∆ соответственно равны гипотенузе и острому углу другого прямоугольного ∆, то такие треугольники равны.
Доказательство (стр. 78): из свойства (сумма двух острых углов прямоугольного треугольника = 90°) следует, что в таких треугольниках два других угла тоже равны, поэтому треугольники равны по второму признаку равенства треугольников, т.е. по стороне (гипотенузе) и двум прилежащим к ней углам. Теорема доказана.
4) Если гипотенуза и катет одного прямоугольного ∆ соответственно равны гипотенузе и катету другого прямоугольного ∆, то такие треугольники равны. (Доказательство на стр. 78)
Средняя линия треугольника. Теорема о средней линии треугольника (доказательство). (стр. 146)
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон
Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство: Пусть MN — средняя линия треугольника ABC. Докажем, что MN||AC и MN=1/2 AC.
Треугольники BMN и BAC подобны по второму признаку подобия треугольников (∠B — общий, BM/BA = BN/BC = 1/2), поэтому ∠1 =∠2 и MN/AC = 1/2. Из равенства ∠1 = ∠2 следует, что MN||AC, а из второго равенства, что MN=1/2AC. Теорема доказана.
