2. Численное решение дифференциальных уравнений и систем.

Для решения дифференциальных уравнений в численном виде пользователям Mathcad предлагается ряд удобных процедур. Среди них выделяется достаточно универсаль­ная процедура odesolve(). В большинстве ситуаций дифференциальное уравнение или система уравнений могут быть решены с помощью этой про­цедуры, причем сам процесс решения достаточно прост.

Общий принцип работы с процедурой odesolve() состоит в следующем. В рамках блока Given задается решаемое уравнение (или система уравнений) с начальными условиями. Заканчивается блок командой вызова процедуры odesolve() с соответствующими аргументами. Таким образом, в численном виде определяется искомая функциональная зависимость (или зависимости).

2.1. Решение дифференциального уравнения с помощью процедуры odesolve().

Простой пример вызова процедуры odesolve() для решения неоднородного дифференциального уравнения второго порядка:

x"(t) + x(t) = sin(t)

Отметим, что при вводе уравнения для начального значения производной символ дифференцирования в виде штриха вводился с помощью комбинации клавиш <Ctrl>+<F7>.

Что касается непосредственно процедуры odesolve(), то в данном случае у нее два аргумента:

• Первый — переменная, которая слу­жит аргументом искомой функции.

• Второй аргумент определяет верхнюю границу (нижняя равна нулю) по аргументу искомой функции.

Решение ищется в соответствующем диапазоне. Результат, возвращаемый процедурой odesolve(), присваивается в качестве значения функции. Функция указыва­ется без аргумента (фактически, аргумент указан при вызове процедуры odesolve ()) — только название.

Найденную в численном виде в результате решения дифференциального уравнения функцию можно протестировать по отдельным точкам (вызывая найденную функцию и указывая значение аргумента), но для наглядности это лучше все же сделать графически. В нижней части Рис. 13 приведен гра­фик, который строится стандартными методами, описанными ранее. При ре­шении системы дифференциальных уравнений ситуация несколько сложнее.

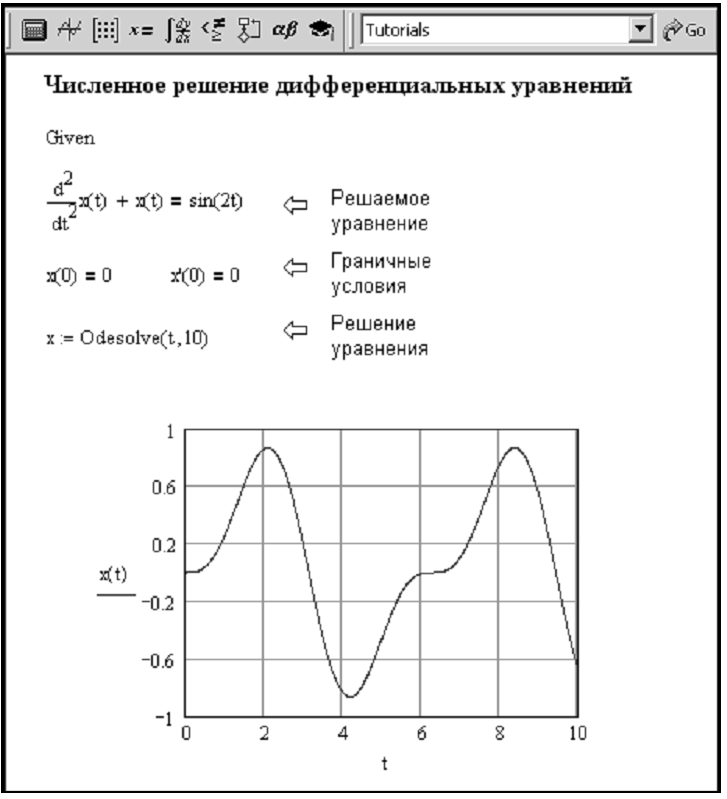
Рис. 13. Решение дифференциального уравнения с помощью процедуры odesolve ().

2.2. Решение системы дифференциальных уравнений odesolve ().

Пример решения системы уравнений представлен на Рис. 14. Системы ре­шаются практически так же, как и отдельные уравнения. В рамках блока Given вводятся решаемые уравнения и начальные условия к ним. После этого вызывают процедуру odesoive (). Отличие по сравнению с предыдущим случаем состоит в том, что теперь аргументов у процедуры не два, а три:

• Пер­вый аргумент — вектор с названиями функций, относительно которых реша­ется система уравнений;

• Вторым аргументом функции указываем перемен­ную;

• А третьим — верхнюю границу ее изменения.

В нижней части документа на Рис. 14 представлены графики найденных функций.

Рис. 14. Решение системы дифференциальных уравнений с помощью процедуры odesolve ().

Еще несколько замечаний относительно процедуры odesoive():

• Что касается ее аргументов, то последним из них можно указывать число шагов для поиска решения.

• Как отмечалось ранее, уравнения могут решаться различными математическими методами. По умолчанию в рамках процедуры odesoive() ре­шение ищется по методу Рунге-Кутта с переменным шагом. Можно задать адап­тивный метод или метод решения жестких уравнений. Для этого нужно выделить процедуру odesoive() и щелкнуть правой кнопкой мыши. В раскрывающемся списке есть несколько команд, позволяющих выбрать требуемый метод решения дифференциальных уравнений: команду Adaptive выбирают для адаптивного метода, а команда stiff полезна при решении жестких уравнений и систем. Процедура выбора команды для метода решения показана на Рис. 15.