Важнейшие функции распределения и теорема Чебышева.

1.Нормальный закон.

Для иллюстрации нормального распределения случайной величины служит доска Гальтона. Такое распределение получается, когда действует множество мелких равноправных конкурирующих случайных причин, вызывающих случайные отклонения. Поскольку подобная ситуация весьма распространена в природе, то нормальный закон имеет исключительное значение.

.

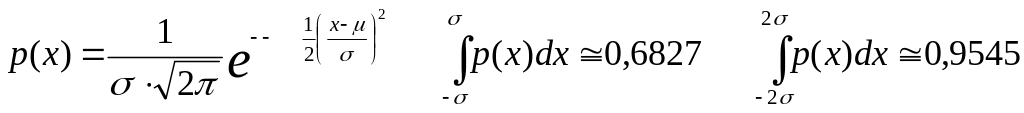
Кривые выглядят как на рис 7. Точки перегиба кривой имеют координаты .

Интервал содержит 99.73% случаев, 1 из 370 вне интервала.

- 95.45% случаев, 1 из 22 вне интервала.

- 68.27% случаев, 1 из 3 вне интервала.

2.Биномиальное распределение.

Пример. Бросание монеты из двух металлов с разными удельными весами.

3.Закон Пуассона.

Для дискретной случайной величины x=m=0,1,2,…

Пример. Капли дождя падают на проволоку так, что вероятностью попадания двух капель в одну точку можно пренебречь, а среднее число капель, упавших на проволоку за час, равно а, то есть, . Это могут быть и другие редкие события: число заявок на АТС ночью, число заявок в билетную кассу ночью, число заявок в ремонтные мастерские ночью, число отказов оборудования в месяц, число число попаданий осколков в малоразмерную цель.

Закон Пуассона получается из биномиального, когда события очень редки, но число испытаний очень велико: .

Для распределения Пуассона дисперсия равна среднему: . Это свойство часто используется для проверки гипотезы о том, что случайная величина распределена по закону Пуассона. Чем точнее выполняется последнее равенство, тем больше оснований принять гипотезу о пуассоновском распределении.

Теорема Чебышева (Чебышев Пафнутий Львович, 1874):

Для любого распределения

Основные понятия математической статистики.

Абрахам Вальд: математическая статистика - совокупность методов, позволяющих принимать наилучшие возможные решения в условиях неопределенности.

Всё теоретически возможное множество случайных величин данной природы называется генеральной совокупностью.

Выборкой называется несколько случайных величин, взятых из генеральной совокупности методом случайного отбора.

Случайный отбор: каждый элемент генеральной совокупности имеет равную вероятность попасть в выборку.

Когда мы осуществляем перенос знаний с выборки на генеральную совокупность, это называется индукцией.

Индукция - переход от частного к общему или экстраполяция (перенос) свойств с части на целое.

Генеральная совокупность - это основная математическая абстракция в математической статистике, количество входящих в неё значений случайной величины равно бесконечности. Иными словами, это математическая модель очень большой исследуемой совокупности, выделенной из реального мира.

Вся возможная информация о случайной величине содержится в её функции распределения. Больше о случайной величине мы в принципе знать не можем.

Основная идея статистического исследования такова:

Нам надо исследовать свойства некой большой совокупности объектов. Все вместе мы их исследовать не можем. Тогда мы делаем из этой совокупности выборку, по этой выборке оцениваем некие характеристики исследуемой совокупности, а затем некими косвенными методами пытаемся оценить достоверность этих оценок. При этом чисто из соображений удобства математических расчетов, исследуемая совокупность может объявляться бесконечной. Такое допущение не приводит к большим погрешностям, если исследуемая совокупность действительно достаточно велика. Как определить, "достаточно" или "не достаточно" она велика? Это зависит от конкретных условий задачи и может сильно варьироваться. Но из опыта известно, что в большинстве практических задач совокупность из 10000 значений можно считать бесконечно большой.

Оценками или статистиками называются числовые значения неких функций, рассчитанные по выборке.

Оценки бывают точечные и интервальные.

Точечные оценки состоят из одного числа, интервальные из трёх чисел: верхняя и нижняя границы интервала и вероятность попадания в него.

Чаще всего используют оценки трех типов: положения, разброса, формы.

Оценки положения характеризуют положение кривой распределения в своих осях.

Оценки разброса характеризуют "размытость", "ширину" функции распределения.

Оценки формы характеризуют асимметрию и эксцесс кривой распределения.

С помощью оценок матстатистика позволяет принимать разумные решения в условиях недостатка информации на основе полученных оценок.

Главное достоинство оценок заключается в том, что они могут быть предсказаны точнее, чем отдельные элементы выборки.

Теоретической базой матстатистики является закон больших чисел:

Разница между фактической и теоретически ожидаемой долей стремится к нулю по мере возрастания числа наблюдений. Иначе: фактические данные всё больше приближаются к теоретическим с ростом числа наблюдений.

На основании сравнения выборок происходит проверка гипотез.

Н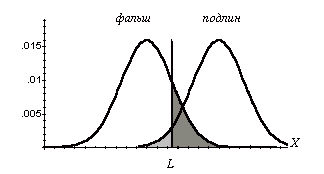 уль-гипотеза Н_о -сигнала нет, отличий нет - консервативная(в Багдаде все спокойно)

Рис 7

Конкурирующая или альтернативная Н_А -противоположна ей.

На рис. 7 L -пороговое значение признака. Если предмет имеет значение этого признака выше, он объявляется подлинным, если ниже - фальшивым. Пусть данный предмет имеет значение признака Х в точности равное L . Светло-серым заштрихована площадь, равная вероятности того, что будет объявлена ложная тревога, то есть подлинный предмет будет объявлен фальшивым. Темно-серым заштрихована площадь, равная вероятности пропуска: подлинным будет объявлен фальшивый предмет.