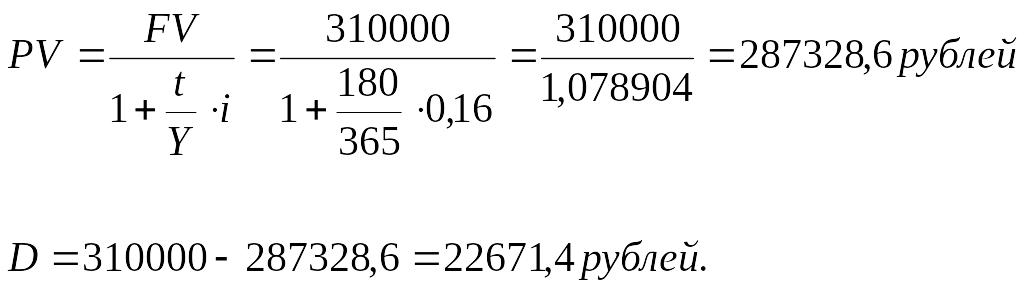2.2 Переменные процентные ставки

В условиях динамично меняющегося состояния финансового рынка при заключении финансового соглашения может быть установлена не только постоянная на весь период финансовой сделки, но и переменная, изменяющаяся во времени процентная ставка.

Предположим, что в течение периода времени установлена ставка простых процентов , тогда приращение капитала за этот период составит .

Если в течение периода времени действует ставка простых процентов , то начисленные за этот период проценты составят .

Пусть число периодов начисления процентов - .

Тогда при установлении переменной, т.е. дискретно изменяющейся во времени процентной ставки, наращенная сумма определяется по формуле:

, (2.3)

где — ставка простых процентов в периоде , где ;

Пример. Банк предлагает вкладчикам следующие условия по срочному годовому депозиту: первое полугодие процентная ставка 12% годовых, каждый следующий квартал ставка возрастает на 2,5%. Проценты начисляются только на первоначально внесенную сумму вклада.

Определите наращенную за год сумму, если вкладчик поместил в банк на этих условиях 400,0 тыс. руб.

Решение:

2.3. Реинвестирование

Если по прошествии некоторого периода зафиксированная к данному моменту наращенная сумма инвестируется вновь, то такая операция называется реинвестированием (повторным инвестированием) или капитализацией полученных на каждом этапе наращения средств. В этом случае проценты начисляют на уже наращенные в предыдущем периоде суммы, т.е. происходит многоразовое наращение.

Предположим, что в течение периода времени установлена ставка простых процентов , тогда к концу этого периода наращенная сумма составит . Затем эта сумма будет помещена наследующий срок под простых процентов. К концу периода наращенная сумма будет равна величине и т.д.

Таким образом, итоговая наращенная сумма определится по формуле:

(2.4.)

где — продолжительность периодов наращения;

- процентные ставки, по которым производится реинвестирование.

Пример. Клиент поместил в банк 500,0 тыс. руб. Какова будет наращенная за 3 месяца сумма вклада, если за первый месяц начисляются проценты в размере 10% годовых, а каждый последующий месяц процентная ставка возрастает на 5% с одновременной капитализацией процентного дохода?

Решение:

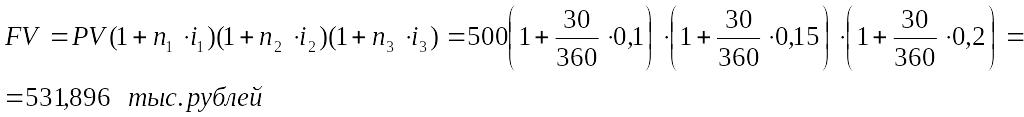
2.4. Математическое дисконтирование по простым процентам

В финансовой практике часто приходится решать задачу, обратную вычислению наращенной суммы, которая может быть сформулирована таким образом: определить сумму , которую необходимо инвестировать в данный момент времени, с тем, чтобы через некоторый определенный период получить при установленной ставке процента требуемую наращенную сумму . Для решения этой задачи применяется операция дисконтирования.

Дисконтирование позволяет по известным наращенной сумме, процентной ставке и сроке финансовой операции определить современную стоимость этой наращенной суммы.

Другими словами дисконтирование позволяет определить, какую первоначальную сумму надо дать в долг, чтобы получить в конце срока сумму при условии, что на долг начисляются проценты по ставке .

В зависимости от вида процентной ставки применяются два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. В первом случае при расчете применяют обычные (декурсивные), а во втором – авансовые проценты.

Рассмотрим, как производится математическое дисконтирование.

Выразив из формулы (2.1) , получим формулу математического дисконтирования:

, (2.5)

Здесь - современная стоимость наращенной (будущей) суммы денег ; - срок проведения финансовой операции (число процентных периодов); - процентная ставка.

Дисконтный множитель показывает, какую долю составляет первоначальная величина долга в его окончательной сумме .

Пример. Заемщик должен возвратить кредит единовременным платежом с процентами за период 2 года. Проценты по кредиту составили 12% годовых. Какую сумму получил заемщик в момент заключения кредитного договора и чему равен дисконт, если сумма к возврату составляет 1 500 000 рублей?

Решение: FV=1500 000 рублей; n=2 года; i= 0,12

,

.

В случае если срок финансовой операции задан в днях или в месяцах, из формулы (2.2) получим формулу математического дисконтирования для <1:

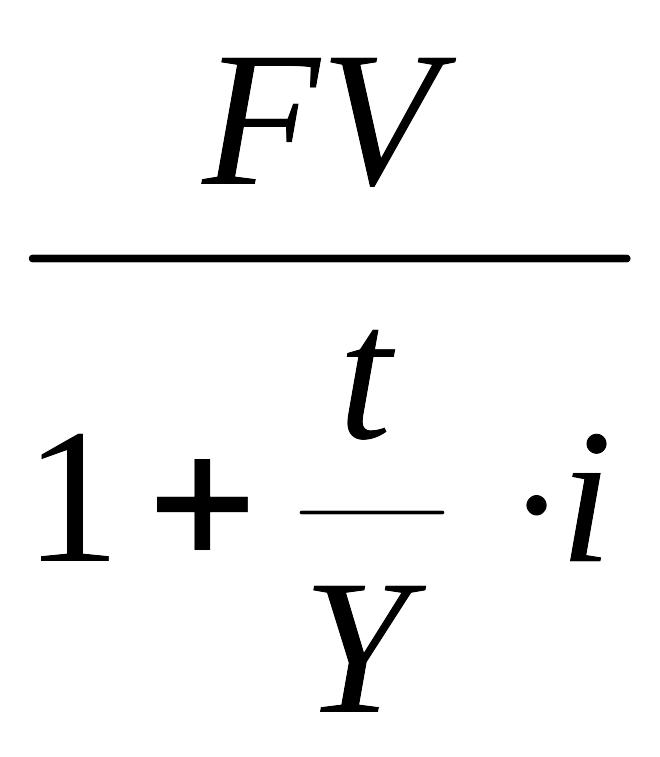, (2.6)

где - длительность финансовой операции в днях (в месяцах); - число дней (месяцев в году).

Пример. Какую сумму инвестор должен внести сегодня под 16% годовых, чтобы через 180 дней после подписания договора накопить 310 тыс. руб. при условии, что начисляются простые точные проценты.

Решение: FV=310 000 рублей; t=180 дней; i=0,16; Y=365 дней.