II.Преобразования координат при переходе к новому базису.

Пусть в n-мерном линейном (векторном) пространстве Rⁿ заданы два базиса:

(старый)

(новый)

Векторы нового базиса выражаются через векторы старого базиса следующим образом:

+ +…+

= + + …+

…………………………………..

= + +…+

Опр. Матрица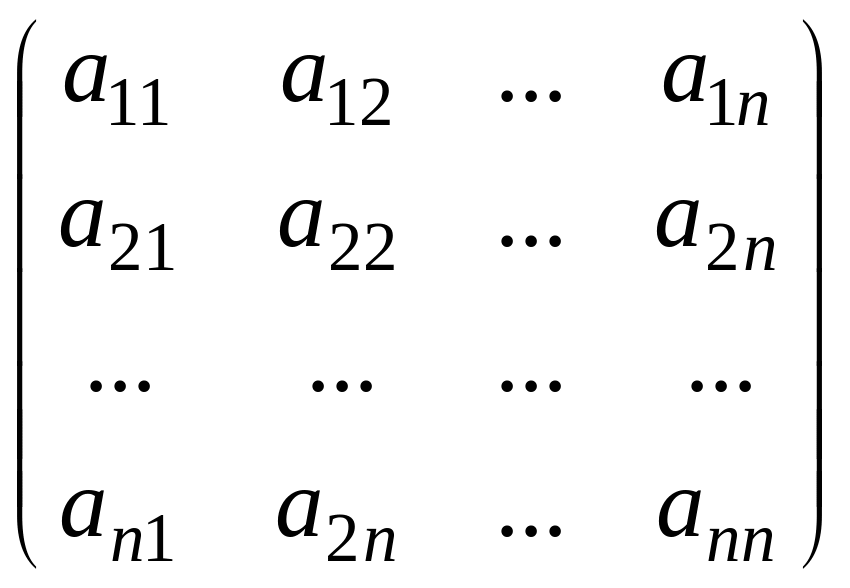 А= называется матрицей перехода от старого базиса , ,…, к новому (или матрицей линейного преобразования). Матрица А – невырожденная (иначе – линейно зависимы, что противоречит определению базиса). Значит для матрицы А обратная А^-1.

Рассмотрим как связаны координаты одного и того же вектора в старом и новом базисах.

Пусть x₁,…,x_n – координаты в старом базисе

,…, – координаты в новом базисе .

= .

Можно доказать:

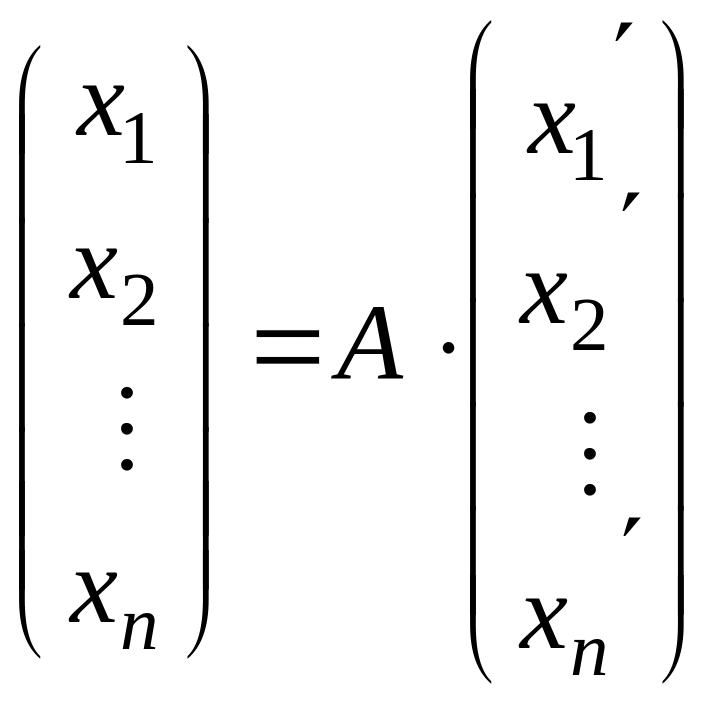, где А – матрица перехода от ,…, к .

или

= А^-1

Эти формулы называются формулами преобразования координат.

Пример 10.1 Пусть вектор имеет координаты (1,-2) в базисе .

Найти координаты этого вектора в базисе , .

§11. Собственные векторы и собственные значения

Опр. Ненулевой вектор называется собственным вектором линейного преобразования А (матрицы А), если найдется такое число , что выполняется равенство

(1)

Число называется собственным значением линейного преобразования А, соответствующим собственному вектору .

Если линейное преобразование А в базисе имеет матрицу

А= ,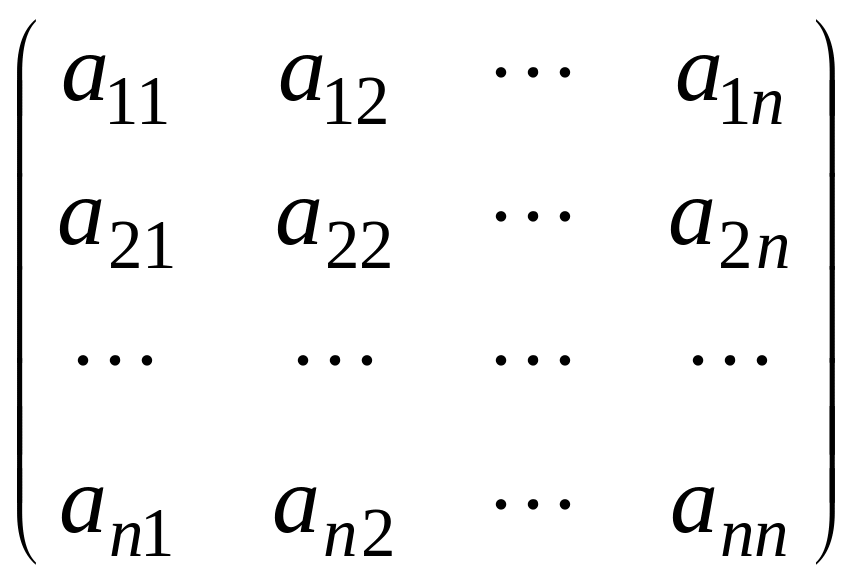

то равенство (1) можно записать в матричной форме

или , где Е – единичная матрица

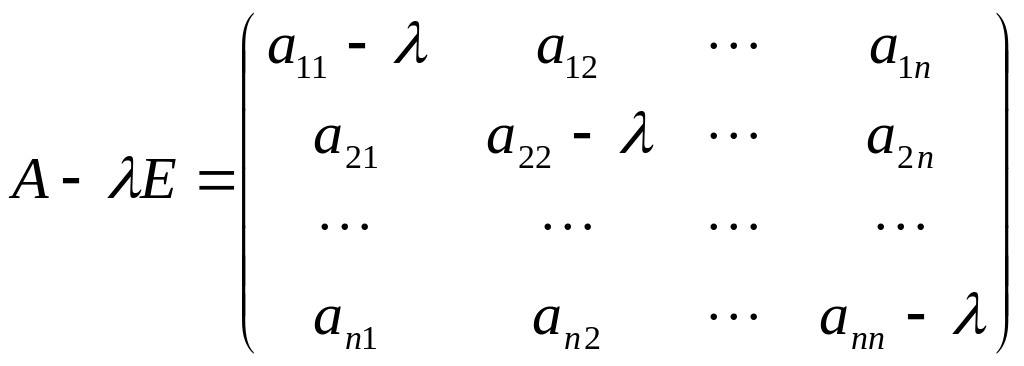, где , Х= .

Перейдем к координатной форме записи

. (2)

Для того чтобы эта однородная система n уравнений с n неизвестными имела ненулевые решения необходимо и достаточно, чтобы ее определитель был равен нулю.

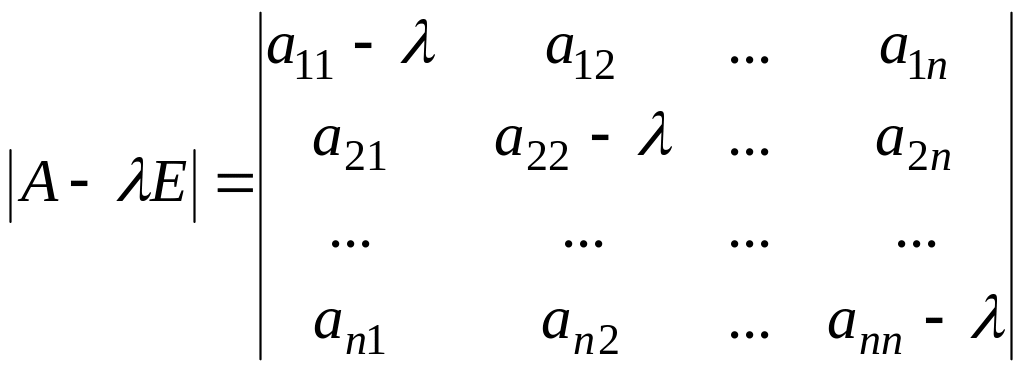=0 (3)

– характеристическое уравнение матрицы А.

Корни характеристического уравнения являются собственными значениями матрицы А (характеристические числа).

Каждому собственному значению соответствует собственный вектор, координаты которого находят из системы (2) при соответствующем значении .

Пример 11.1 Найти собственные значения и собственные векторы матрицы. А =

Пример 11.2 Найти собственные значения и собственные векторы матрицы.

А=

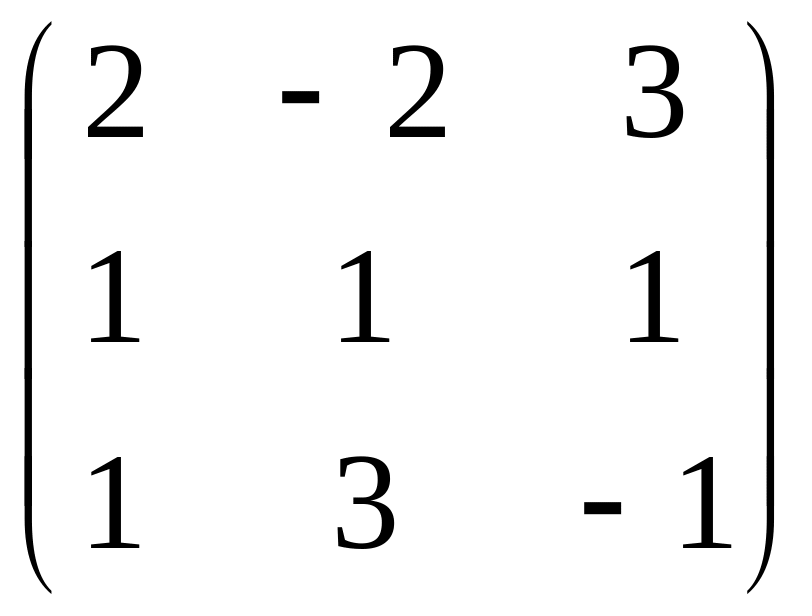
Опр. Квадратная матрица А называется симметричной относительно главной диагонали, если а_ij=a_ji.

Все корни характеристического уравнения симметричной матрицы действительны.

Теорема. Для того чтобы матрица А в некотором базисе была диагональной необходимо и достаточно, чтобы этот базис состоял из собственных векторов матрицы А.

, где Т – матрица, столбцы которой состоят из собственных векторов.

16