
2.2. Формула трапеций и формула Симпсона
Из предельного соотношения
(2.3) следует, что теоретически при больших
погрешность в формуле
прямоугольников(2.2) будет маленькой. Но
в большинстве задач для достижения
требуемой точности
![]() число разбиений
отрезка
придется выбирать очень
большим. Это может повлечь за собой
появление ошибки, связанной с накоплением
ошибок округления (если просуммировать
1000 слагаемых, каждое из которых имеет
ошибку округления
число разбиений
отрезка
придется выбирать очень
большим. Это может повлечь за собой
появление ошибки, связанной с накоплением
ошибок округления (если просуммировать
1000 слагаемых, каждое из которых имеет
ошибку округления
![]() ,
то суммарная ошибка может составить
величину порядка
,
то суммарная ошибка может составить
величину порядка
![]() ,
т.е. хотя каждое слагаемое будет иметь
только 5 верных знаков после запятой,
однако сумма будет иметь только 2 верных
знака после запятой). В связи с этим на
практике используются более точные
формулы: трапеций и Симпсона.
,
т.е. хотя каждое слагаемое будет иметь
только 5 верных знаков после запятой,
однако сумма будет иметь только 2 верных
знака после запятой). В связи с этим на
практике используются более точные
формулы: трапеций и Симпсона.
Для формулы трапеций
аппроксимирующая функция
выбирается кусочно-линейной:
отрезок интегрирования разбивается
(как это было указано в п. 2.1) на
равных частей точками
,
и на каждом из отрезков
функция
есть линейная функция,
график которой соединяет точки
![]() и
и
![]() ,
как это
указано на рис.2.4.
,
как это
указано на рис.2.4.
Т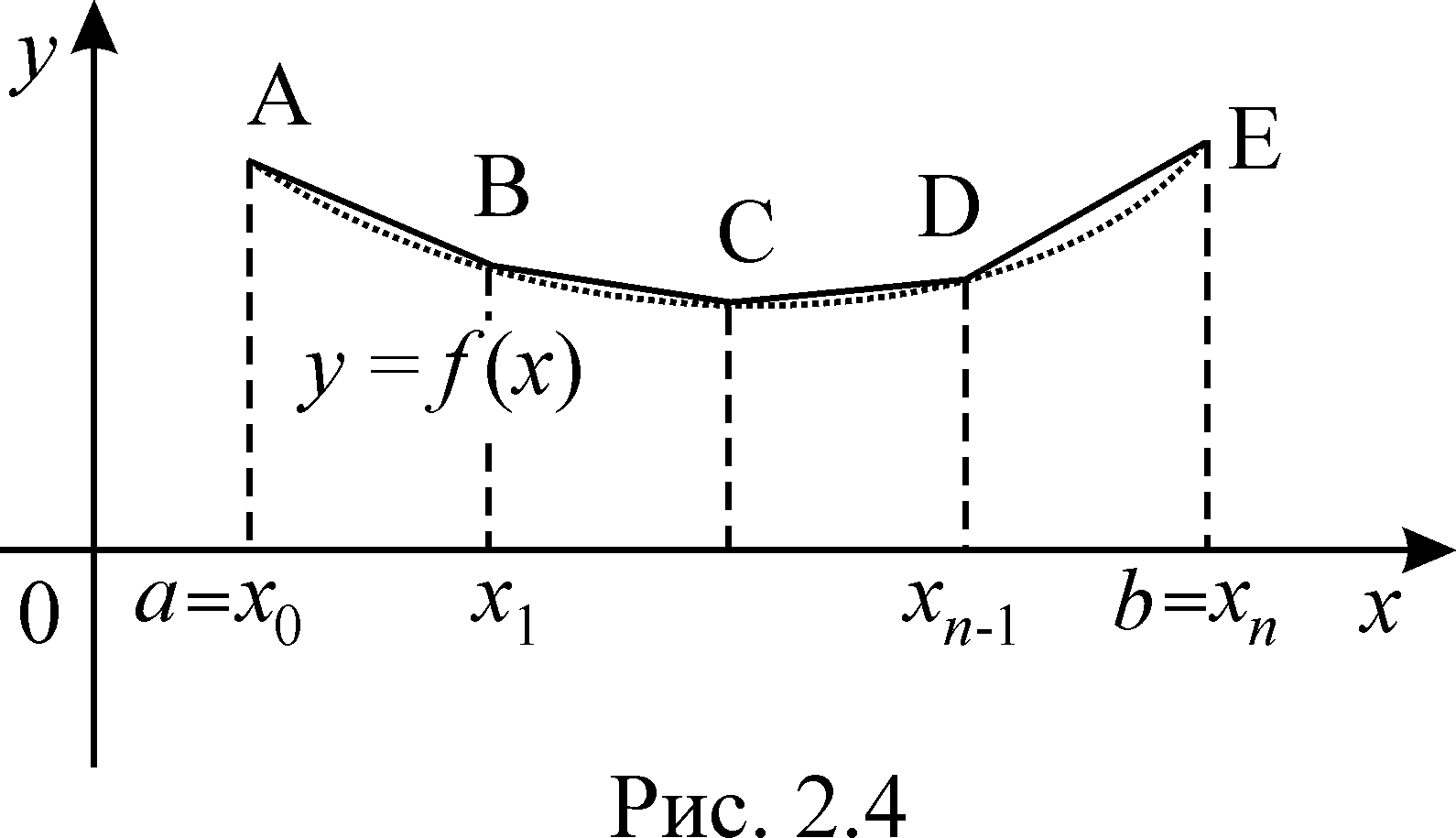 огда
огда
![]() есть сумма площадей трапеций
есть сумма площадей трапеций
![]() ,
,
![]() ,ограниченных
осью Oх,
прямыми
,ограниченных
осью Oх,
прямыми
![]() ,
,
![]() и графиком аппроксимирующей функции
(на рис. 2.4 это ломаная
АBСDЕ).
Следовательно,
и графиком аппроксимирующей функции
(на рис. 2.4 это ломаная
АBСDЕ).
Следовательно,
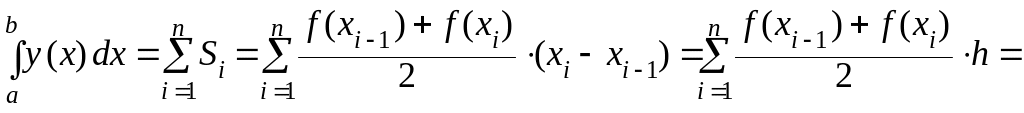
![]()
Таким образом, формула трапеций имеет вид:
![]() ,
где
,
где
![]() (2.4)
(2.4)
С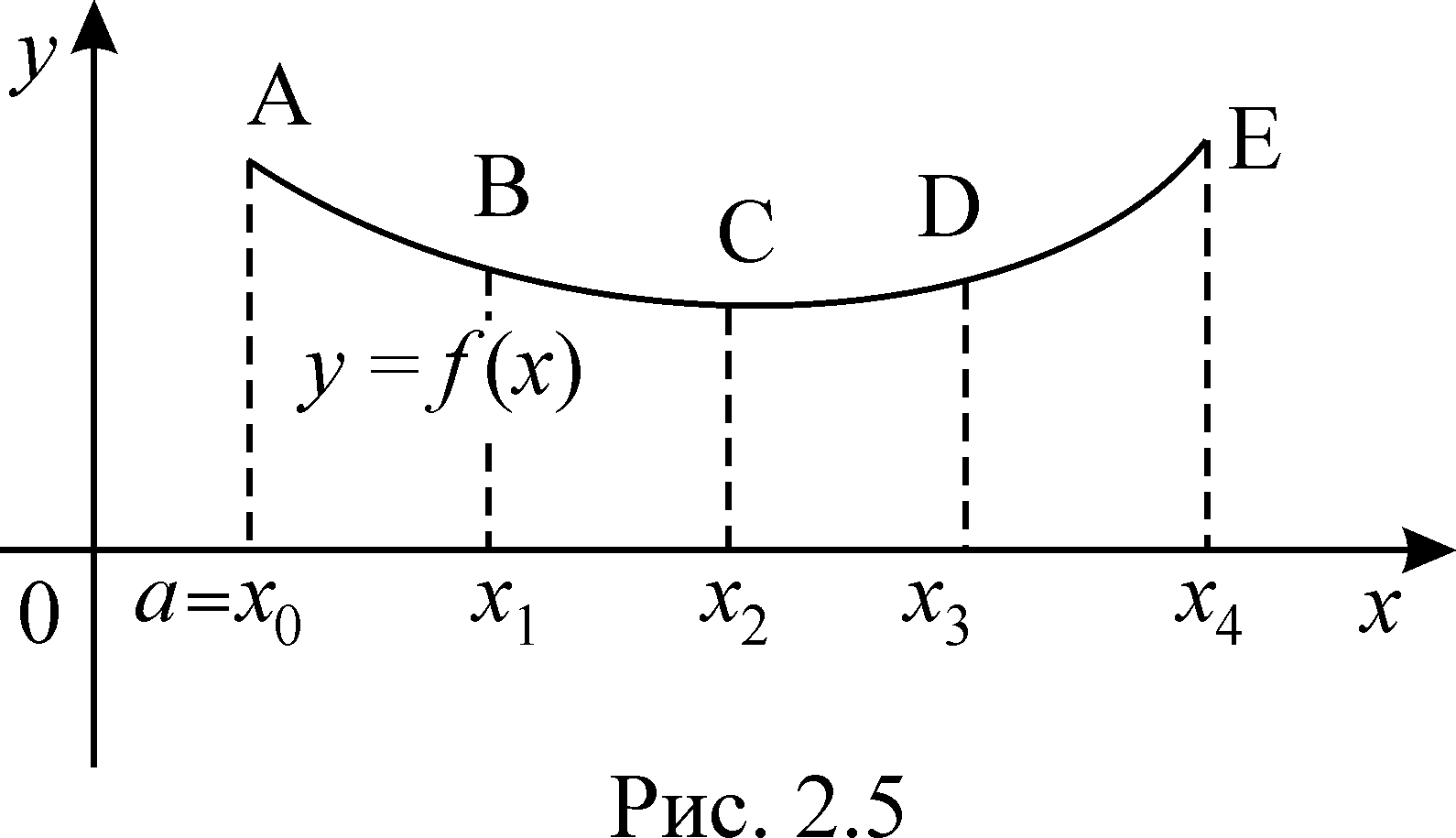 равнивая
рис.2.4 и рисунки для формулы прямоугольников,
можно ожидать, что при одном и том же
формула (2.4) дает меньшую погрешность,
чем формула (2.2).
равнивая
рис.2.4 и рисунки для формулы прямоугольников,
можно ожидать, что при одном и том же
формула (2.4) дает меньшую погрешность,
чем формула (2.2).
Еще более точной является формула Симпсона. Если в методе трапеций используется приближение подынтегральной функции кусочно-линейной функцией, то в формуле Симпсона используется параболы в качестве аппроксимирующих функций (поэтому его еще называют методом парабол). Рассмотрим принцип построения аппроксимации в методе Симпсона по сравнению с методом трапеций (см. рис 2.5).
Как известно, через любые 3 точки на
плоскости, не лежащие на одной прямой,
можно провести единственную параболу
(если точки лежат на одной прямой, то
парабола вырождается в эту прямую).
Таким образом, нам следует сначала
провести параболу (то есть подобрать
коэффициенты квадратичной функции
![]() )
через точки A, B,
C, затем через точки C,
D, E и так
далее. На рис. 2.5 сами параболы не
нарисованы, потому как они будут
располагаться очень близко к точкам
графика подынтегральной функции
,
чего нельзя сказать про рис.2.4, где
заметна явная разница между графиками
подынтегральной и аппроксимирующей
кусочно-линейной функции. Таким образом,
для применения метода Симпсона отрезок
интегрирования следует всегда разбивать
на четное число частей.
)
через точки A, B,
C, затем через точки C,
D, E и так
далее. На рис. 2.5 сами параболы не
нарисованы, потому как они будут
располагаться очень близко к точкам
графика подынтегральной функции
,
чего нельзя сказать про рис.2.4, где
заметна явная разница между графиками
подынтегральной и аппроксимирующей
кусочно-линейной функции. Таким образом,
для применения метода Симпсона отрезок
интегрирования следует всегда разбивать
на четное число частей.
Вычислим
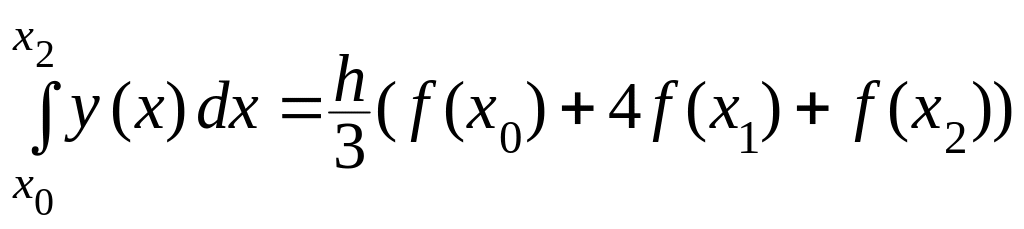 (проверьте!),
(проверьте!),
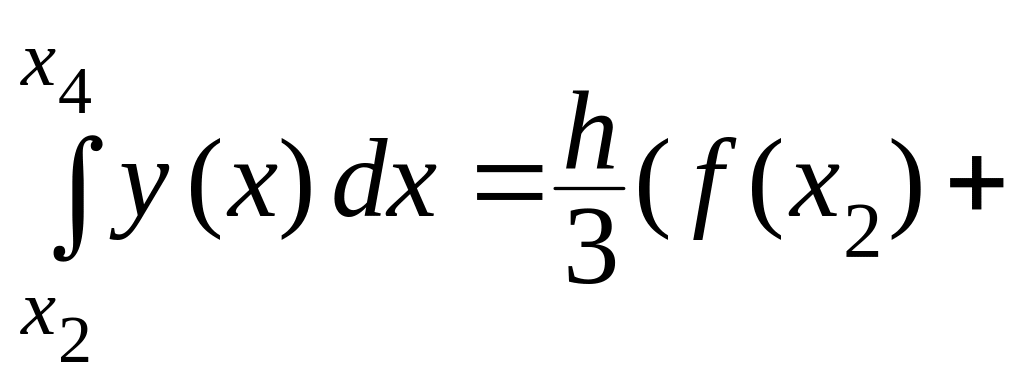
![]() и т.д. Таким образом,
и т.д. Таким образом,
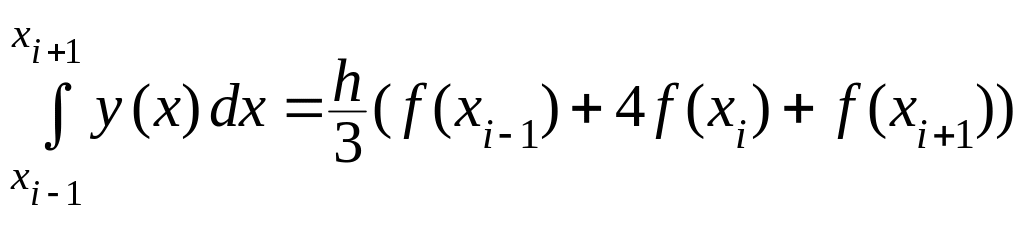 .
(2.5)
.
(2.5)
Тогда получим формулу
Симпсона:
![]() ,
где
,
где
![]() ,
(2.6)
,
(2.6)
причем - четное.
Упражнение 1. Записать, как будет определяться функция на отрезке для случая формулы трапеций.
Упражнение 2.
Записать, как будет определяться функция
на отрезке
![]() для случая формулы Симпсона.
для случая формулы Симпсона.
Упражнение 3. Обосновать равенство(2.5).
Упражнение 4. Получите из (2.5) формулу (2.6).
Упражнение 5.
Докажите, что если
,
то последовательность
![]() будет приближающей для точного значения
интеграла.
будет приближающей для точного значения
интеграла.
Упражнение 6.
Докажите, что если
![]() ,
то последовательность
,
то последовательность
![]() будет приближающей для точного значения
интеграла.
будет приближающей для точного значения
интеграла.
