Лабораторная работа № 2

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

2.1. Общие сведения

Как известно, если функция непрерывна на отрезке и известна ее первообразная , то для вычисления определенного интегра­ла используется формула Ньютона-Лейбница . Однако во многих задачах первообразную найти невозможно (так называемые, неберущиеся интегралы) или процедура ее нахождения является слишком сложной. В частности, теория дает алгоритм на­хождения первообразной, если подынтегральная функция есть рациональная дробь. Но в случае, когда многочлен в знаменателе этой рациональной дроби имеет большую степень, данный алгоритм крайне сложно реализовать.

Вследствие этого вычисление определенного интеграла по формуле Ньютона-Лейбница может быть затруднительным или даже практически невыполнимым. Кроме того, на практике подынтеграль­ная функция часто задается таблично (как результат изме­рений в процессе опытов), и тогда само понятие первообразной те­ряет смысл. Поэтому, важное значение имеют приближенные (численные) методы вычисления определенного интеграла.

Обычный прием численного интегрирования состоит в том, что данную подынтегральную функцию заменяют аппроксимиру­ющей (приближающей) функцией простого вида, а затем приближенно полагают

, (2.1)

причем функция должна быть такова, чтобы интеграл справа в (2.1) можно было вычислить непосредственно.

2.2 Формула прямоугольников

Самая простая формула численного интегрирования - форму­ла прямоугольников. В этом случае аппроксимирующая функция выбирается кусочно-постоянной: отрезок интегрирования разбивается на отрезков одинаковой длины точками (узлами)

,

где , (узлы являются равноотстоящими, а число называется шагом вычислений), и на каждом полуинтервале (либо ) значение приближающей функции полагают постоянным , где - фиксированная точка из отрезка . Тогда

,

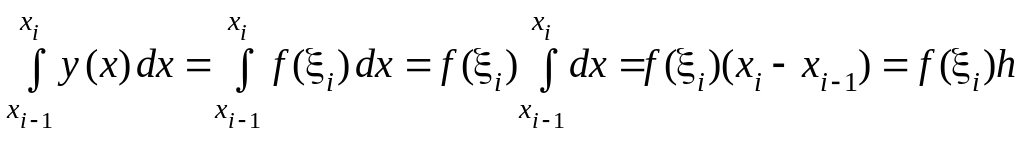и мы получаем .

Заметим, что, так как приближающая функция зависит от количества отрезков разбиения , то и приближенное значение интеграла также будет зависеть от . Таким образом, можно записать формулу прямоугольников в следующей форме:

. (2.2)

Если подынтегральная функция непрерывна на отрезке интегрирования ( ), то числа (при любом выборе местоположения точек ) образуют приближающую последовательность для точного значения интеграла, т.е.

. (2.3)

О бычно точки выбирают по определенному правилу. Например, в качестве можно брать левые концы отрезков (в этом случае получаем формулу левых прямоугольников) или правые концы этих отрезков (формула правых прямоугольников) или середины отрезков (формула средних прямоугольников). В частности, формулу левых прямоугольников можно записать так: . Ее геометрическая интерпретация приведена на рис.2.1-2.3.

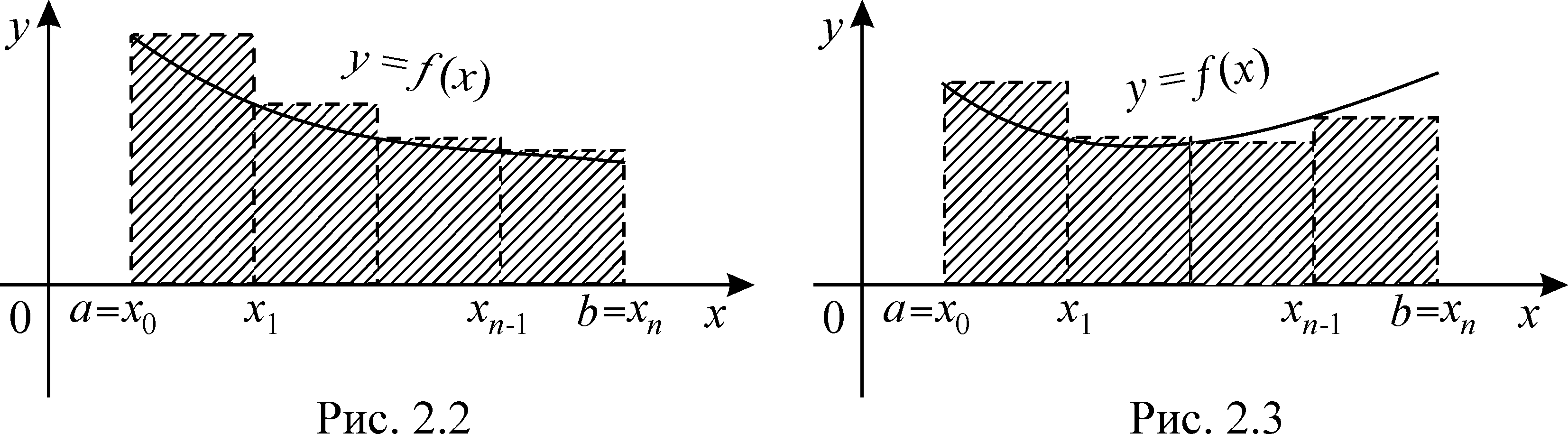
Площадь криволинейной трапеции, образованной графиком функции , осью Ох и прямыми и , заменяется на площадь заштри­хованных прямоугольников. Из рисунков видно, что для возрастающей функции при любом n значения всегда меньше искомого интеграла, для убывающей – больше.

Упражнение 1. Обоснуйте равенство 2.3.

Упражнение 2. Запишите формулы правых и средних прямоугольников и дайте их геометрическую интерпретацию.