3.1. Дискретизация сигнала и построение выборки
В современной системе связи информация передается в цифровой форме. Такое представление универсально для любого вида информации. Его основой является теорема отсчетов, или теорема Котельникова, по которой любой сигнал с ограниченным спектром может быть представлен совокупностью отсчетов (выборкой) – мгновенными значениями через определенный интервал времени t. Множество таких значений называется выборкой; математическая форма записи которой следующая:
(20)
где
функция Дирака.
Исходный сигнал может быть представлен по выборке с помощью ортогонального ряда Котельникова:
(21)
Система связи должна передать выборку любым способом, однако чаще это реализуется при цифровом представлении сигнала. Такая оцифровка выполняется аналогово-цифровым преобразователем (АЦП). Обычно информация на выходе АЦП представлена в параллельном коде, который для передачи необходимо преобразовать в последовательный. Эта операция (рис. 3.1) реализуется специальными микросхемами – преобразователями, построенными на регистрах сдвига.
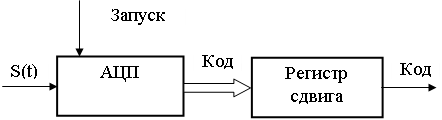
Рис. 4. Сигналы АЦП
Основные характеристики АЦП – частота запуска и разрядность выходного кода. Именно их и надо определить по спектру сигнала и шуму квантования.
В приемнике по выборке можно восстановить исходный сигнал различными способами, например при помощи фильтра низких частот с граничной частотой с, равной верхней частоте сигнала.
Интервал дискретизации заданного сигнала по времени определяется на основе теоремы Котельникова по неравенству:
|
(22)
|
где Fв = c / 2 – верхнее значение частоты спектра сигнала. Обычно Δt берут с запасом в несколько раз (как минимум 2-3 раза).
Построение выборки детерминированного сигнала не представляет каких – либо трудностей, а для случайного сигнала необходимо построить временную функцию. Это построение идет в следующей последовательности.
а) Создадим последовательность чисел распределенных по заданному закону. В среде Mathcad это вектор размерностью m; для его формирования имеются следующие встроенные функции.
rnorm (m,μ,σ). Нормальный закон распределения, m – размерность вектора, μ - среднее значение, σ – среднеквадратичное отклонение.
runif (m,a,b). Равномерное распределение , a и b граничные точки интервала a<b и a<m<b
rexp(m,r). Экспоненциальное распределение, r – параметр распределения, r,x>0.
rgamma(m,s). Гамма-распределение, s – параметр масштаба (m,s>0).
Предупреждение. В программах Mathcad массивы ограничены в зависимости от версии, поэтому рекомендуем принимать значение массива не более 30.
б) Далее будем считать, что эти значения появляются последовательно во времени с шагом равным интервалу дискретизации Δt. Создадим массив чисел с этим шагом такой же размерности, что и массив случайных чисел.
в) Построим функцию сигнала.
В приложении 4 в качестве примера показана эта процедура на примере нормального распределения.