3. В аудитории.

1. Вычислить криволинейные интегралы 1-го рода:

1.1 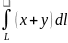, где - контур треугольника с вершинами (Д. 4221);

1.2 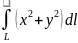, где - кривая: 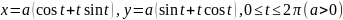(Д. 4223);

1.3 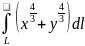, где - дуга астроиды: (Д. 4225).

2. Найти длину дуги пространственной криво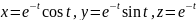й при 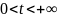(Д. 4232).

3. Вычислить криволинейные интегралы 1-го рода, взятые вдоль пространственных кривых:

3.1 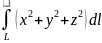, где - часть винтовой линии: 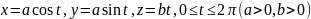(Д. 4237);

3.2 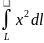, где – окружность: 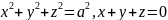(Д. 4238).

4. Задачи для самостоятельной работы.

1. Вычислить криволинейные интегралы 1-го рода:

1.1 , где - арка циклоиды: (Д. 4222);

1.2 , где - дуга гиперболы: 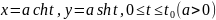(Д. 4224);

1.3 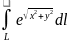, где - выпуклый контур, ограниченный кривыми: 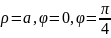( и – полярные координаты) (Д. 4226).

1.4 Найти массу кривой: 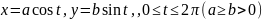, если линейная плотность в ее точке равна 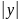(Д. 4241/1)

2. Найти длину дуги пространственной кривой от точки до точки 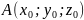(Д. 4233).

3. Вычислить криволинейные интеграл 1-го рода 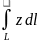, взятый вдоль пространственной кривой, где – коническая винтовая линия (Д. 4239).

Занятие 6. Тема: «Криволинейный интеграл 2-го рода, формула Грина, приложения».

1. Определение криволинейного интеграла 2-го рода. Пусть – простая, спрямляемая незамкнутая кривая на координатной плоскости задана уравнениями

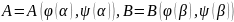, . (5.9)

Пусть на кривой заданы две функци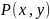и: и 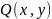. Разобьем на частей точками . При этом кривая разобьется на частей точками 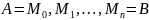в направлении от к . Пусть 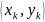- координаты точки 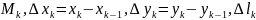- длина дуги . На каждой дуге возьмем некоторую точку и составим две интегральные суммы:

.

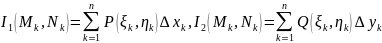Определение 5.2 Число называется пределом интегральных сумм при , если такое, что для любого разбиения кривой , у которого , и для любого выбора промежуточных точек выполняется неравенство .

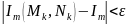Если существует 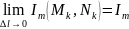, то он называется криволинейным интегралом 2-го рода и обозначается .

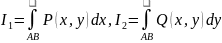Сумма называется общим криволинейным интегралом 2-го рода и обозначается так:

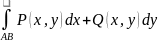(5.10)

Аналогично водится криволинейный интеграл 2-го рода вдоль пространственной кривой, заданной параметрически (5.4) :

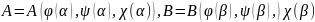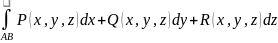. (5.11)

Из определения криволинейного интеграла 2-го рода следует, что при изменении направления обхода кривой изменяется и знак интеграла, т.е.

.

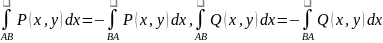Если - замкнутая кривая, т.е. точка совпадает с точкой , то для нее можно указать два направления обхода от к . Если область, лежащая внутри контура, остается слева по отношению к движущейся по контуру точке, то такое направление обхода кривой называется положительным, а противоположное ему – отрицательным.

Криволинейные интегралы 2-го рода обладают свойствами линейности и аддитивности, однако теорема об оценке модуля интеграла и формула среднего значения, вообще говоря, неверны.

2. Вычисление криволинейного интеграла 2-го рода с помощью определенного интеграла.

Теорема 5.2 Если - кусочно гладкая кривая, заданная уравнениями (5.1) ((5.4) для пространственной кривой), функции 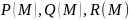кусочно непрерывны вдоль кривой , то существует криволинейный интеграл (5.10)((5.11)) и справедливо равенство

, (5.12) для пространственной кривой

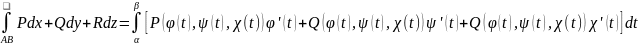. (5.13)

Пример 5.7 Вычислить криволинейный интеграл 2-го рода 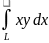по кривой , пробегаемой в направлении возрастания параметра , - дуга синусоиды .

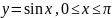∆ Воспользуемся теоремой 5.2, параметризуем кривую: 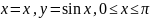. Получим: .∆

Пример 5.8 Вычислить криволинейный интеграл 2-го рода 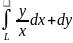по кривой , пробегаемой в направлении возрастания параметра , - дуга синусоиды .

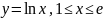∆ Так как: , то:

.∆

Пример 5.9 Вычислить криволинейный интеграл 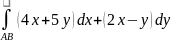по отрезку , ориентированному от точки 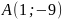к точке .

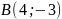∆ Уравнение прямой, проходящей через точки и , имеет вид:

,

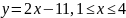следовательно, 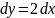и

. ∆
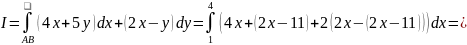
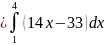