2. Свойства ортонормированного базиса.

1) В ортонормированном базисе скалярное произведение двух элементов и равно сумме попарных произведений их координат;

(4.2.9)

2) В произвольном базисе пространства скалярное произведение двух элементов: и определяется равенством:

, (4.2.10)

где матрица имеет элементы: .

3) Для того, чтобы в данном базисе евклидова пространства скалярное произведение любых двух элементов было равно сумме попарных произведений соответствующих координат этих элементов, необходимо и достаточно, чтобы базис был ортонормированным.

4) Пусть:

, (4.2.11)

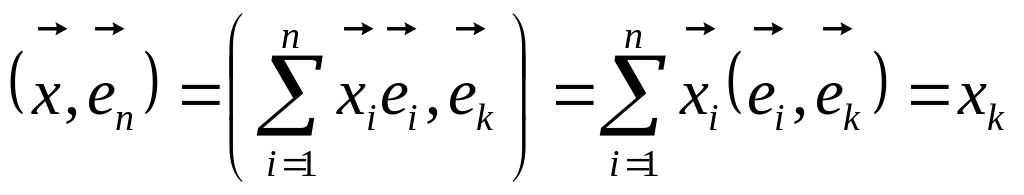. (4.2.12)

Координаты произвольного элемента относительно ортонормированного базиса равны скалярным произведениям этого элемента на соответствующие базисные векторы.

Произвольный ортонормированный базис обладает свойствами, аналогичными свойствам прямоугольного декартового базиса.

3. Разложение - мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения. Пусть - произвольное подпространство - мерного евклидова пространства .

Определение. Совокупность всех элементов пространства , ортогональных к любому элементу подпространства называется ортогональным дополнением подпространства .

Ортогональное дополнение само является подпространством пространства . Это утверждение справедливо, поскольку из ортогональности всех элементов к элементу следует ортогональность элементу любой линейной комбинации элементов .

Справедливо следующее утверждение: Всякое - мерное евклидово пространство представляет собой прямую сумму своего произвольного подпространства и его ортогонального дополнения .

Доказательство. Выберем в подпространстве произвольный ортонормирован­ный базис . Этот базис можно дополнить элементами пространства до базиса во всем . Проведя процесс ортогонализации элементов , , мы получим ортонормированный базис во всем пространстве . Пусть - произвольный элемент пространства . Если разложить его по базисным элементам, получим:

. (4.2.13)

Из (4.2.13) видно, что элемент однозначно представим в виде:

, (4.2.14)

где

(4.2.15)

вполне определенный элемент подпространства , а

(4.2.16)

вполне определенный элемент ортогонального дополнения подпространства , так как каждый из ортогонален любому элементу . А потому любому из этих элементов ортогональна и линейная комбинация .

4. Изоморфизм - мерных евклидовых пространств. Поскольку в евклидовых пространствах введены операции сложения элементов, умножения элемента на число и скалярное умножение элементов, можно сформулировать следующее определение.

Определение. Два евклидовых пространства и называются изоморфными, если между элементами этих пространств можно установить взаимно однозначное соответствие так, что если элементам соответствуют элементы , то элементу соответствует элемент , элементу соответствует элемент (для любого вещественного ); скалярное произведение равно скалярному произведению : .

Евклидовы пространства изоморфны, если они изоморфны как линейные пространства и если их изоморфизм сохраняет величину скалярного произведения соответствующих пар элементов.

Теорема 4.4. Все евклидовы пространства одной и той же размерности изоморфны между собой.

Доказательство. Достаточно доказать, что любое мерное евклидово пространство изоморфно евклидову пространству упорядоченных совокупностей из вещественных чисел со скалярным произведением

. (4.2.17)

Согласно теореме 4.3 в евклидовом пространстве существует ортонормированный базис . Каждому элементу

(4.2.18)

пространства поставим в соответствие вещественных чисел . Но совокупность вещественных чисел есть вполне определенный элемент

(4.2.19)

пространства .

Установленное соответствие является взаимнооднозначным. Кроме того, из теоремы 2.4 следует, что если элементам и в пространстве соответствуют элементы и в пространстве , то элементу

(4.2.20)

в пространстве соответствует элемент

(4.2.21)

в пространстве , а элементу в пространстве соответствует элемент в пространстве .

Остается доказать, что для соответствующих пар элементов и сохраняется величина скалярного произведения. Действительно:

. (4.2.22)

Так как то имеем:

. (4.2.23)

С другой стороны имеет место соотношение (4.2.17). Теорема доказана.

Доказанная теорема позволяет сделать вывод о том, что, если в каком-нибудь конкретном мерном евклидовом пространстве доказана теорема, сформулированная в терминах операций сложения элементов, умножения элемента на число и скалярного перемножения элементов, то эта теорема справедлива в совершенно произвольном мерном евклидовом пространстве .