10.1.2 Задача Діріхле для кулі.

Знайти гармонічну усередині кулі функцію, яка на межі приймає задані значення.

.

Підготовчий матеріал.

Поліноми Лежандра.

А) твірна функція поліномів Лежандра:

, де х – параметр.

1)Якщо

В околі точки - аналітична, тому подається степеневим рядом, коефіцієнти якого залежать від .

(1)

Функції - функції Лежандра, а - твірна функція поліномів Лежандра. Відомо, що

– коефіцієнти Тейлора;

2) Радіус збіжності ряду (1) є відстань від точки О до найближчої особливої

Знайдемо особливі точки функції :

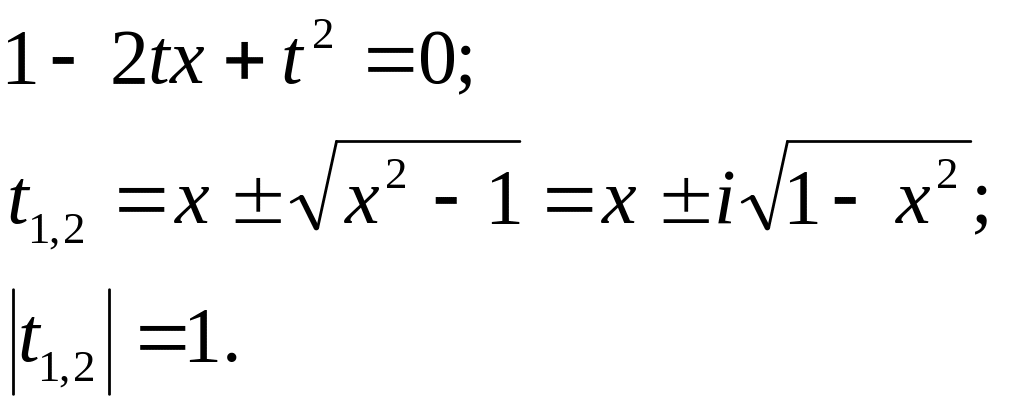
При довільних значеннях особливі точки лежать на одиничному колі, тому радіус збіжності степеневого ряду дорівнює 1.

y Зауваження 1: якщо х=1 , то твірна функція

1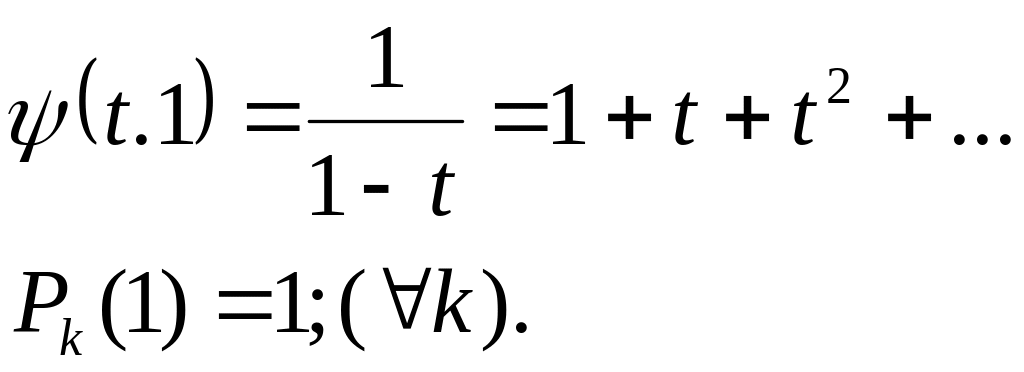

1 x Зауваження 2: якщо х=-1 , то маємо

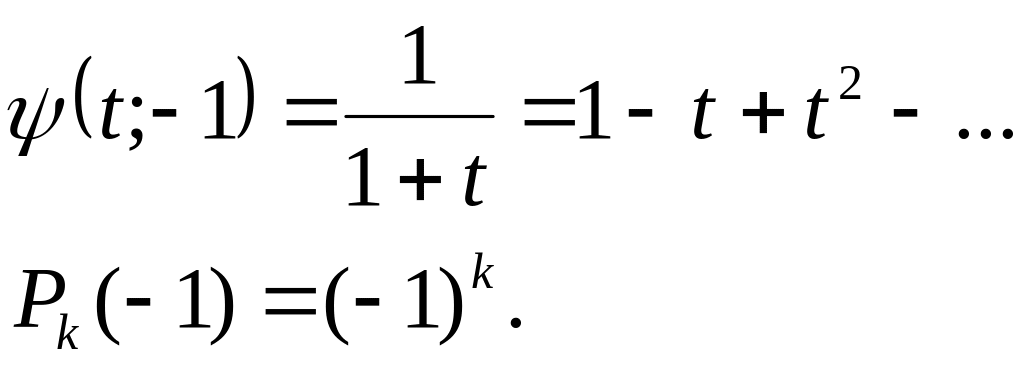
Б) Властивості функцій Лежандра.

1) Функції є поліномами степеня які подаються у вигляді:

.

Доведення властивості.

Користуємось інтегральною формулою Коші для аналітичних функцій:

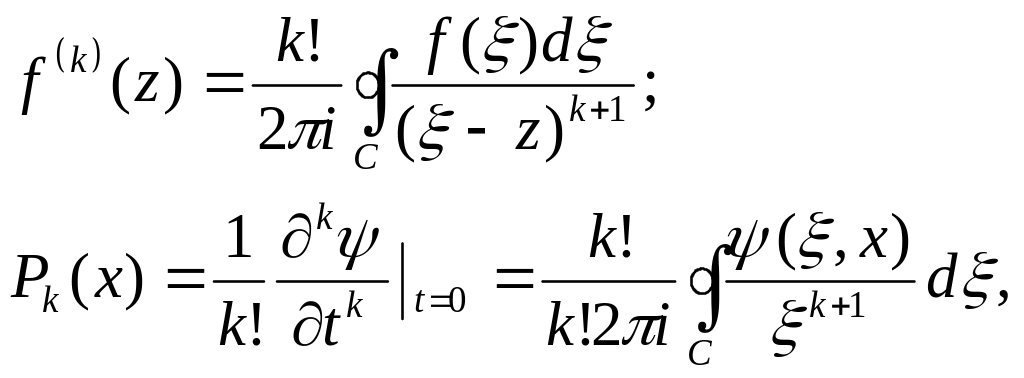
Усередині контура лежить точка О. В останньому інтегралі виконуємо заміну змінної: .

Після такої підстановки останній інтеграл зводиться до вигляду:

, точка х лежить усередині контура .

На основі формули для похідної можемо записати, що:

.

2. Поліноми Лежандра ортогональні на .

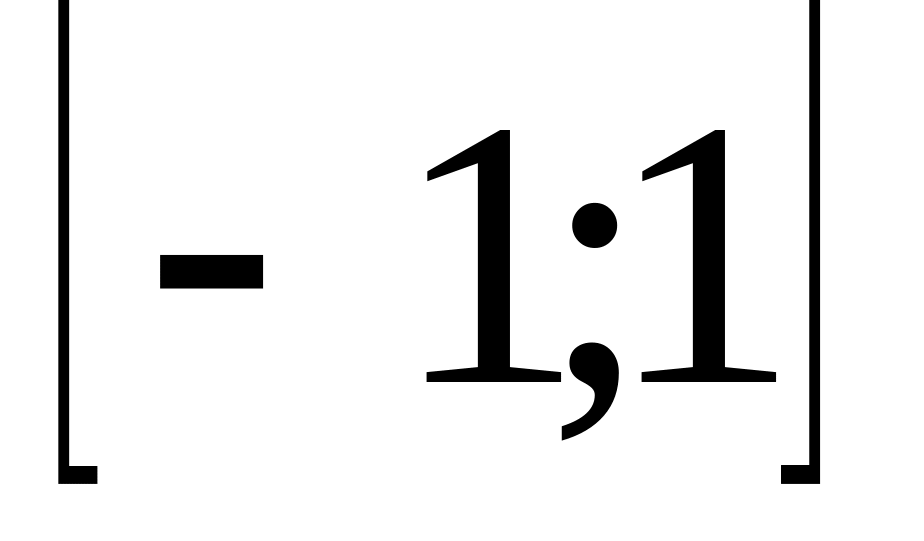3) Інтеграл від квадрата функції (квадрат норми):

.

4) Поліноми Лежандра задовольняють диференціальне рівняння:

, - (лінійне диференціальне рівняння II-го порядку – диференціальне рівняння Лежандра).

Зауваження.

Поліноми Лежандра можна дістати шляхом ортогоналізації системи функцій:

Приклад. Перевірити чи ортогональні дані функції на проміжку :

а) ; б) ; в) ; г) ;

а)

б)

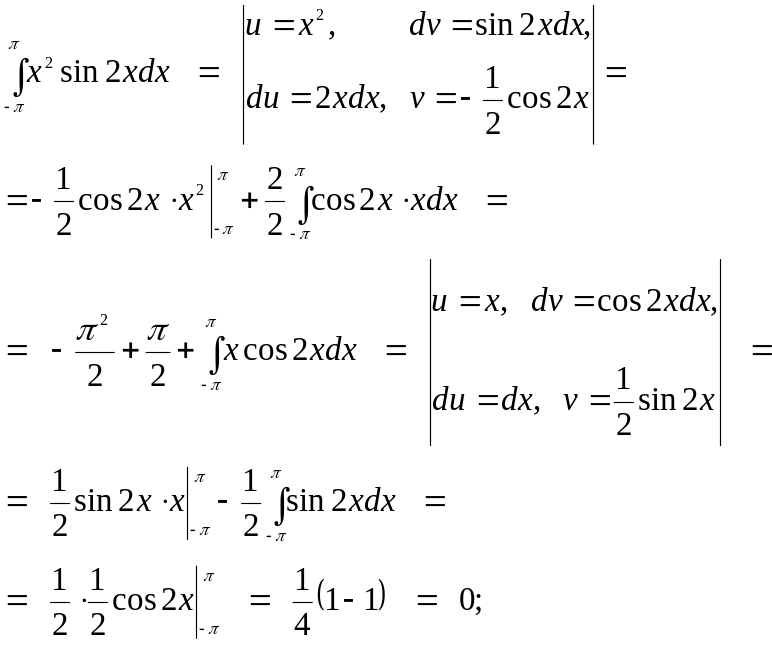
в)

г)

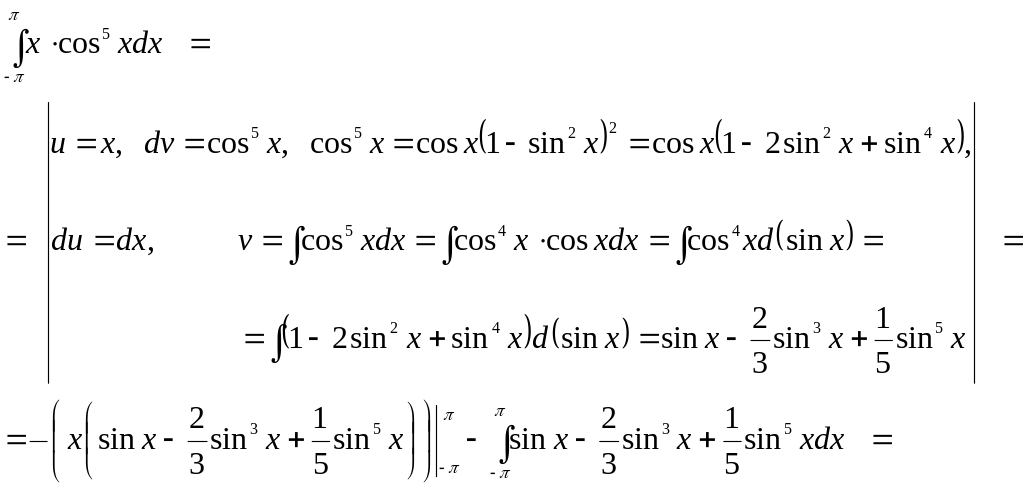
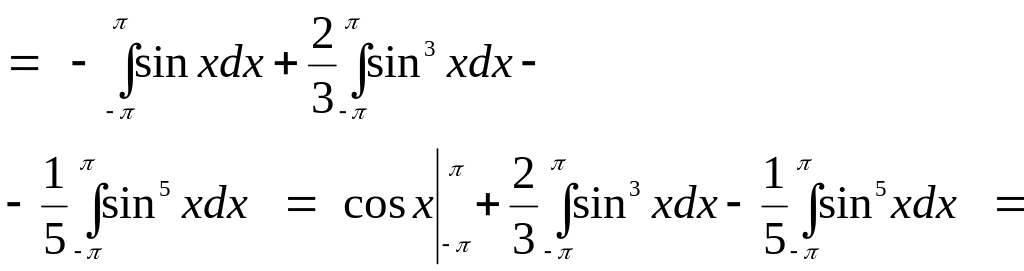
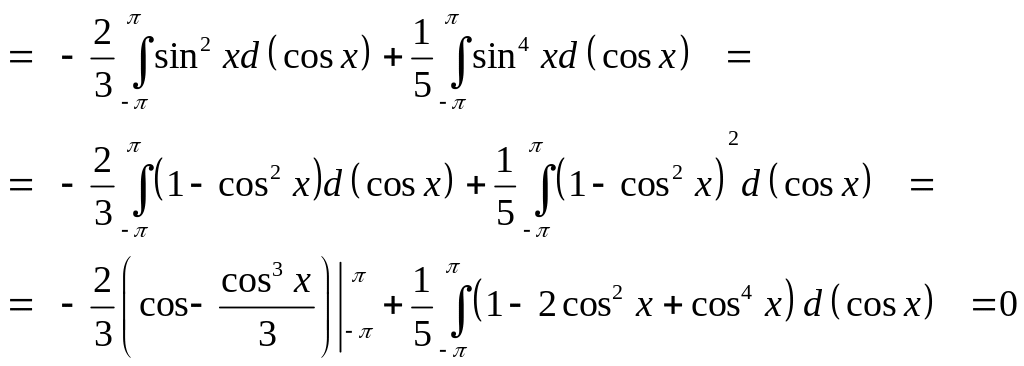
10.1.3 Розв’язання задачі Діріхле.

Розв’язуємо у сферичних координатах для осесиметричного випадку; при цьому .

У випадку осесиметричності функція залежить від і : ; тому

Метод розв’язання(Метод Фур’є).

1).

Підставляємо в рівняння і отримуємо:

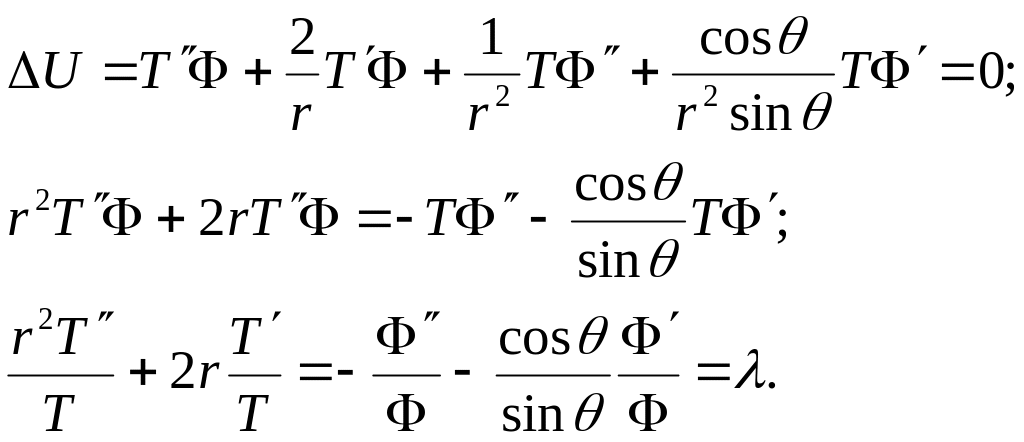
Рівняння зводиться до двох диференціальних рівнянь II-го порядку.

а) Розв’язок першого рівняння шукаємо у формі:

;

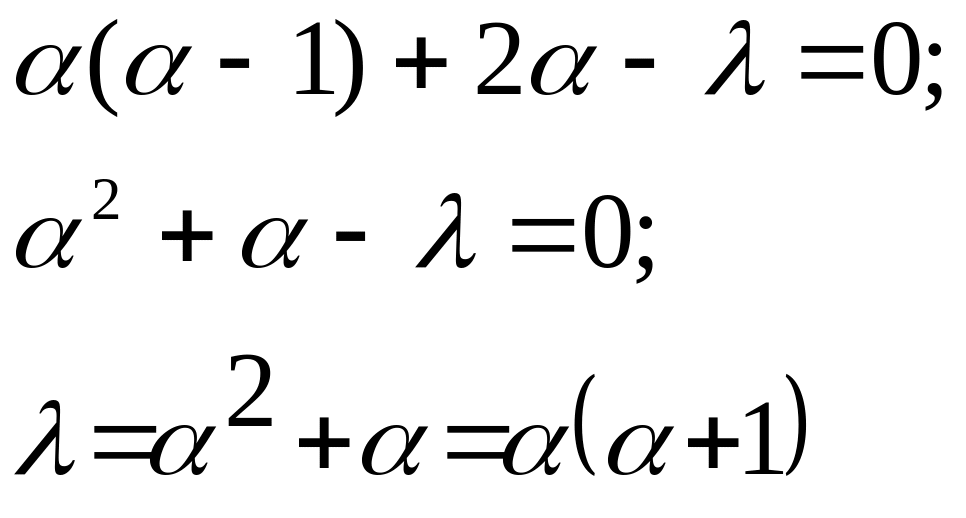Можна довести, що обмежений розв’язок у цьому випадку дістанемо якщо – ціле невід’ємне число, Тоді

Оскільки ми шукаємо обмежений розв’язок, то , тоді .

б) У другому рівнянні виконуємо заміну змінної:

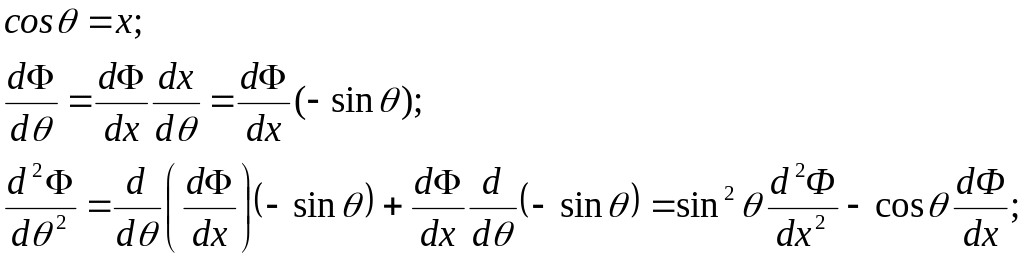
Друге рівняння системи:

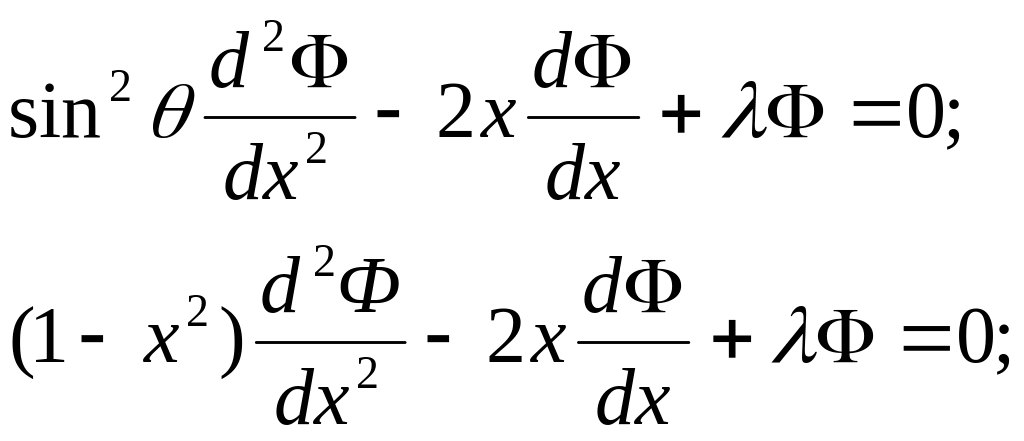
– рівняння Лежандра.

Розв’язком цього рівняння є

в)

– розв’язок рівняння Лапласа.

2)

– умова на межі.

Останню рівність помножимо на й інтегруємо по сфері радіуса R. Дістаємо:

Обчислюємо інтеграл справа

.

(*)

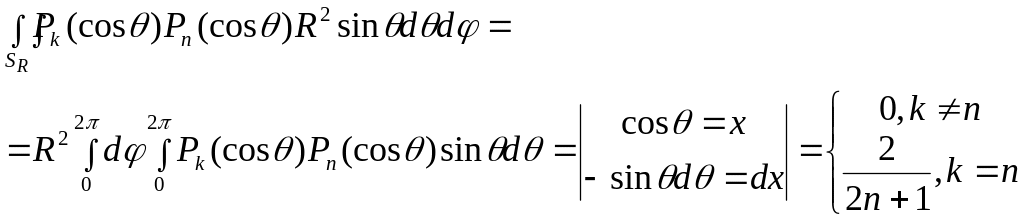Висновок: Розв’язок задачі Діріхле для кулі подається у вигляді ряду

, де – обчислюються за формулою (*).

Зауваження: Цей результат зручно використовувати, якщо функція

_{подана через поліноми Лежандра.}