6 Задания к лабораторной работе

1. Используя разработанную программу, найти приближённые значения интеграла I для заданной табл. 3 функции разными методами с числом разбиений n=10,20,50,100.

2. Рассчитать относительные погрешности 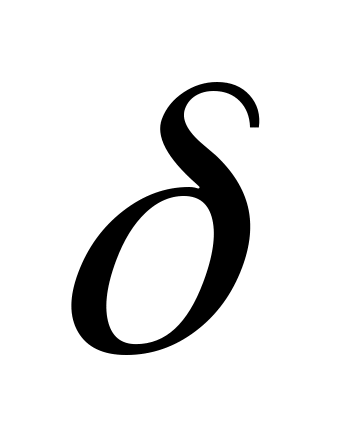для каждого вычисления относительно аналитического решения. Результаты оформить в виде таблицы и представить графически семействами кривых для каждого метода в одном масштабе.

3. Увеличивая число интервалов интегрирования для методов трапеции и Симпсона, постарайтесь найти примерное значение n, для которого модули погрешности ограничения и округления равны.

4. Используя разработанную программу, вычислить I, используя метод Гаусса с тремя и четырьмя ординатами.

5. Сделать выводы по работе, подтвердив их данными таблицы и расчётами.

Примечание: при вычислениях принять .π ⁄ 2=1,5708 рад.

7 Содержание отчета

1 Цель работы.

2 Краткие теоретические сведения об особенностях методов численного интегрирования, граф-схемы алгоритмов.

3 Результаты численного интегрирования, расчеты, таблицы и графики.

4 Выводы по лабораторной работе, подтвержденные данными таблицы, графиками и расчётами.

8 Контрольные вопросы.

1. Привести формулы для вычисления интегралов методами правых, средних и левых прямоугольников.

2. Как оценить погрешности ошибки интегрирования для метода прямоугольников и трапеций?

3. В чём сходство и отличие метода трапеций и метода Симпсона? Привести формулу для вычисления интегралов методом Симпсона.

4. Как изменяются ошибки округления и ограничения при увеличении n ?

5. Чем отличается метод Гаусса от других рассмотренных методов интегрирования?

Лабораторная работа №3

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ

Цель лабораторной работы – закрепить на практике следующие подразделы темы «интерполирование функций»:

• основные понятия теории аппроксимации;

• постановка задачи интерполирования;

• интерполяционный многочлен Лагранжа;

• методы интерполирования Ньютона;

• погрешность интерполирования;

• интерполяционный полином Чебышева;

• аппроксимация сплайнами и с помощью кусочных полиномов.

В результате проведения лабораторной работы студенты должны

знать:

• особенности применения и алгоритмы реализации различных методов численного интерполирования;

• влияние шага интерполирования и расположения узлов на точность интерполирования;

• практические подходы к выполнению интерполяционных вычислений различными методами.

уметь выбирать и реализовывать методы численного интерполирования в соответствии с поставленной задачей, с требуемой точностью и трудоемкостью реализации алгоритмов вычислений.

1 Понятие о приближении функции

Пусть у является функцией от х. Это означает, что любому значению х из области определения поставлено в соответствие значение у. Вместе с тем, на практике часто неизвестна явная связь между х и у, т.е. невозможно записать эту связь в виде некоторой зависимости y=f(x). В некоторых случаях даже при известной зависимости y=f(x) она настолько громоздка (например содержит трудно вычисляемые выражения, сложные интегралы и т.п.), что ее использование в практических расчетах затруднительно.

Наиболее распространенным случаем является задание этой связи в виде некоторой таблицы {x_i, y_i}. Это означает, что дискретному множеству значений аргумента {x_i} поставлено в соответствие множество значений функции {y_i}, i=0, 1,..., n. Эти значения – либо результаты расчетов, либо экспериментальные данные. На практике нам могут потребоваться значения у и в других точках, отличных от узлов x_i. Однако получить эти значения можно лишь путем очень сложных расчетов или проведения дорогостоящих экспериментов.

Таким образом, для экономии времени и средств мы приходим к необходимости использования имеющихся табличных данных для приближенного вычисления искомого параметра у при любом значении (из некоторой области) параметра х, поскольку точная связь y=f(x) неизвестна.

Этой цели и служит задача о приближении (аппроксимации) функций:

данную функцию f(x) требуется приближенно заменить (аппроксимировать) некоторой функцией (х) так, чтобы отклонение (х) от f(x) в заданной области было наименьшим. Функция (х) при этом называется аппроксимирующей. Для практики весьма важен случай аппроксимации функции многочленом

(x) = a₀ + a₁x + a₂x² + ... + a_mx^m

В дальнейшем будем рассматривать лишь такого рода аппроксимацию. При этом коэффициенты a_i будут подбираться так, чтобы достичь наименьшего отклонения многочлена от заданной функции.

Если приближение строится на заданном дискретном множестве точек {x_i}, то аппроксимация называется точечной. К ней относится интерполирование, среднеквадратичное приближение и др. При построении приближения на непрерывном множестве точек (например, на отрезке [a, b],) аппроксимация называется непрерывной, или интегральной.