Примеры

8.3. Найти плотность состояний электронного газа в пленке площадью S с непроницаемыми гранями.

Двумерный электронный газ существует, в частности, в полупроводниковой гетероструктуре, образованной слоем толщиной с запрещенной зоной шириной , находящемся между слоями с запрещенной зоной . В потенциальной яме глубиной до 0,4 эВ существуют энергетические уровни .

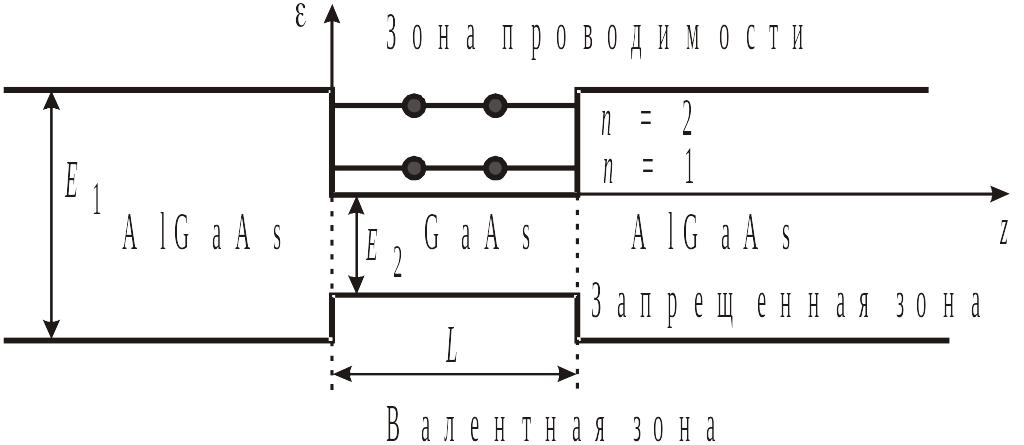
Ось z перпендикулярна поверхности пленки. В приближении бесконечно глубокой потенциальной ямы шириной L используем

, , , (П.8.3)

где 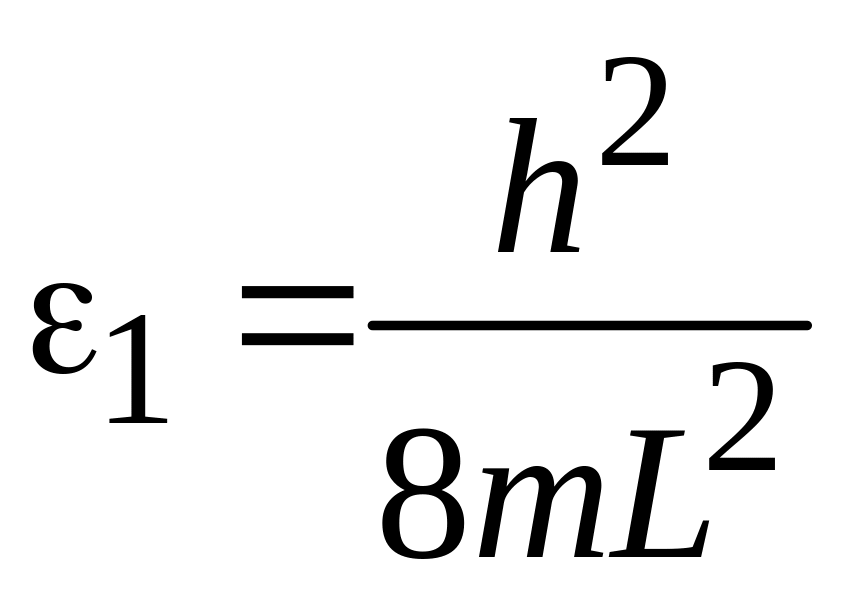, . Сравнивая (П.8.3) с (3.6), находим , . Используя (3.7) и учитывая , , получаем плотность состояний на уровне энергии n:

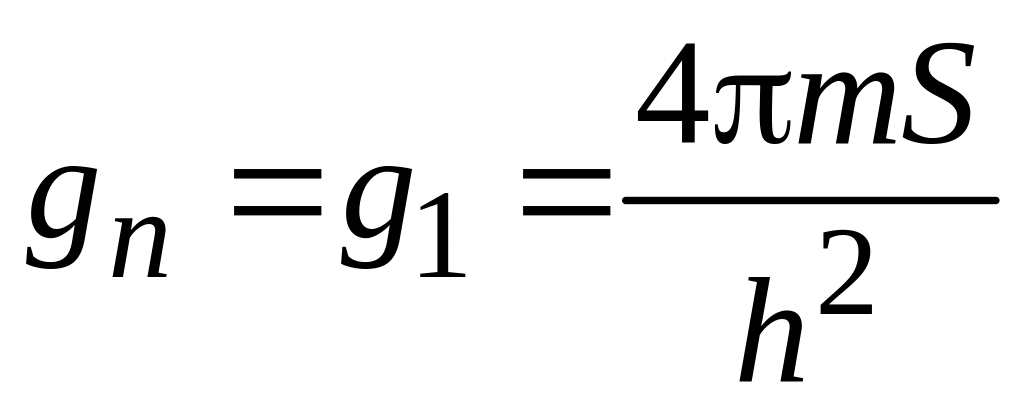. (П.8.4)

В двумерной системе плотность состояний активизированного уровня не зависит от его энергии. Для энергии  число активизированных уровней находим из (П.8.3): , тогда плотность состояний

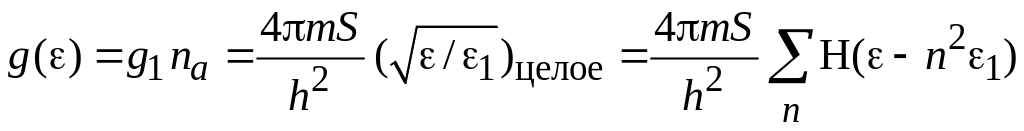. (П.8.4а)

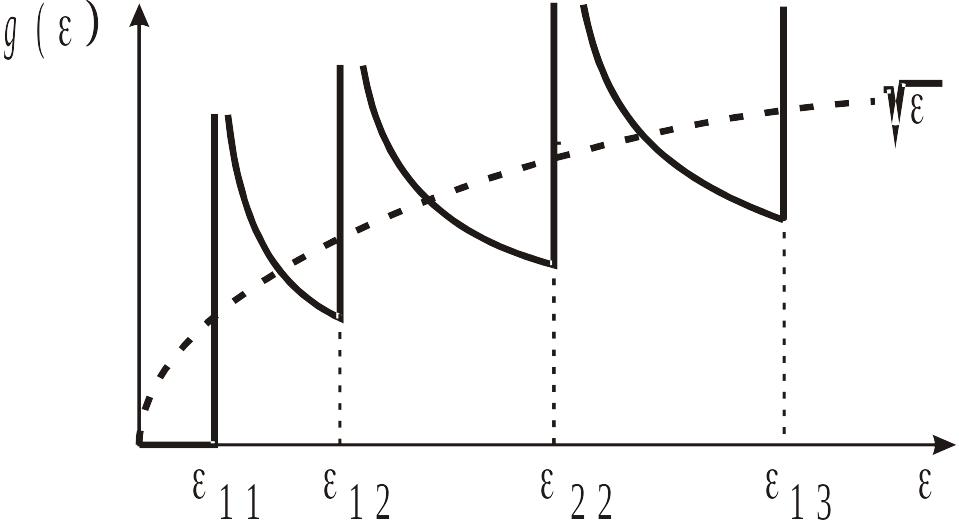
Пунктирная кривая на рисунке – . Плотность состояний увеличивается скачком на величину g₁ каждый раз, когда энергия достигает разрешенного уровня , и частицы начинают заполнять его, увеличивая продольный импульс (рис. 3.4). В точке перехода на очередной уровень продольный импульс обращается в нуль, а поперечная составляющая p_z скачком увеличивается на .

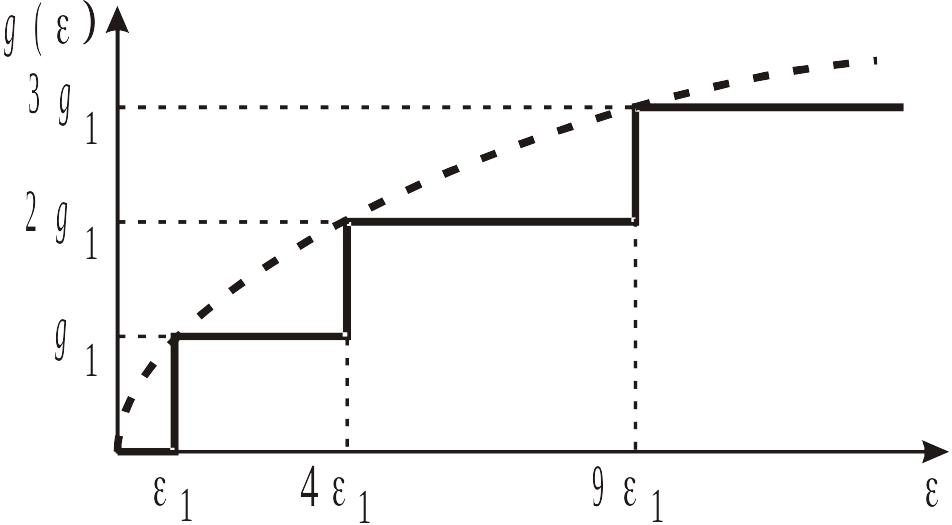
Плотность состояний в пленке

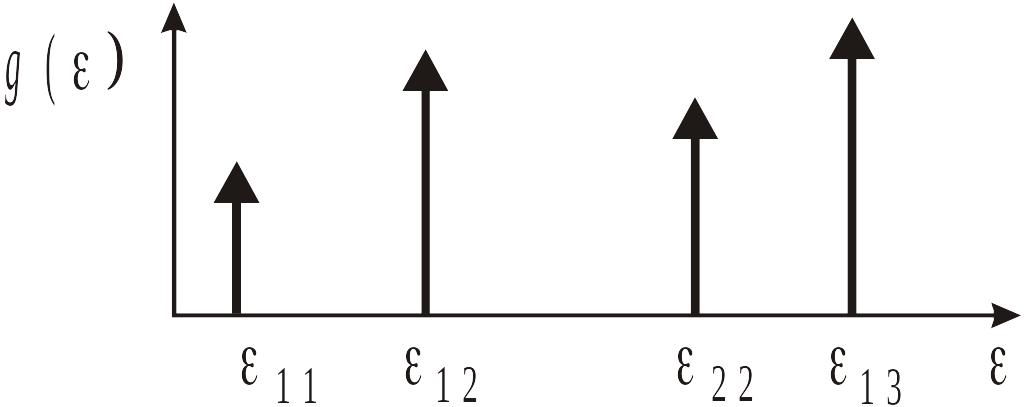
Активизированные уровни (4₁ <  < 9₁)

8.4. Найти плотность состояний электронного газа в квантовой нити.

Ось z направлена вдоль нити. Энергия электрона

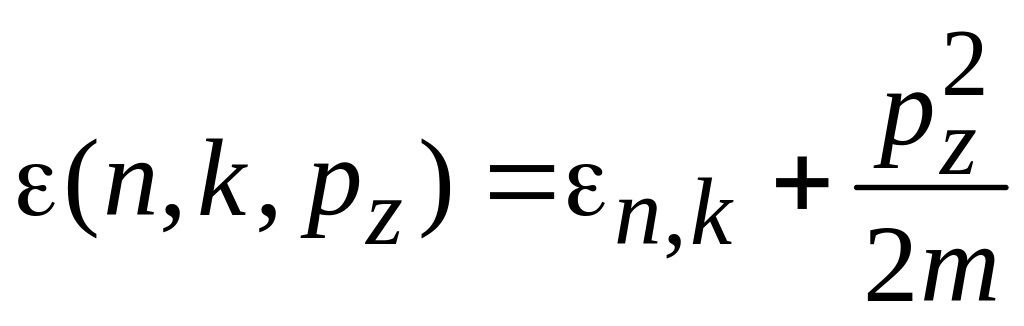, (П.8.5)

где – уровни энергии, связанные с поперечным к нити движением, ; – импульс продольного движения. Сравнивая (П.8.5) с (3.6), находим , . Учитывая и , получаем плотность состояний активизированного уровня с квантовыми числами n и k:

.

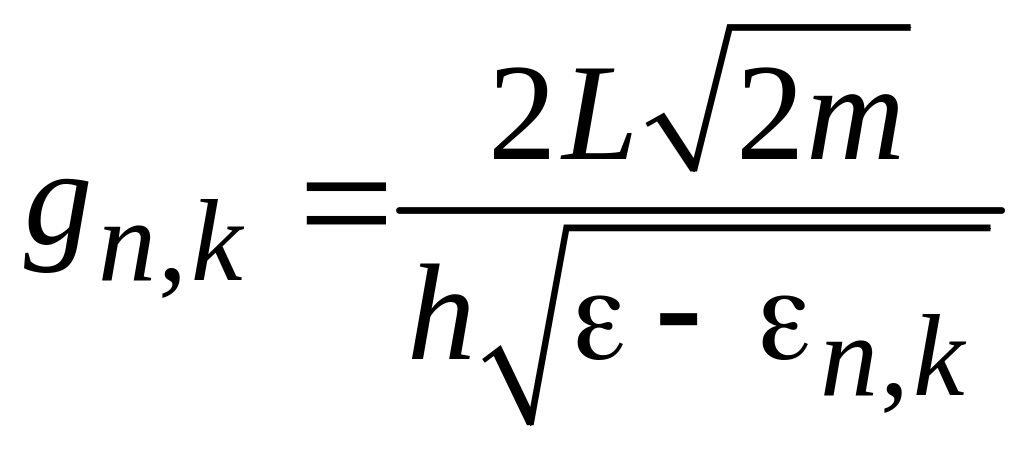Аналогично (П.8.4а), для энергии  находим плотность состояний

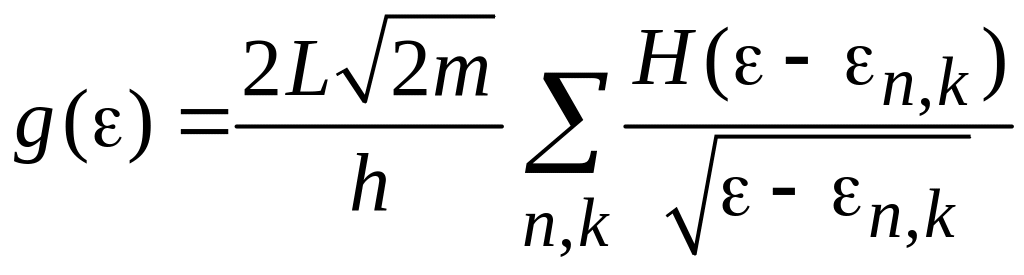. (П.8.6)

8.5. Найти плотность состояний электронного газа в квантовой точке с энергетическим спектром .

Квантовая точка (КТ) является полупроводниковым нанокристаллом с поперечником L ~ (1 – 100) нм во внешней среде с близким значением постоянной решетки и большей шириной запрещенной зоны. Поэтому КТ является потенциальной ямой с числом уровней ~ (2 – 3) и с расстоянием между уровнями . При нормальной температуре электроны занимают низшие состояния. Это обеспечивает температурную стабильность КТ. Расстояние между КТ ~ 100 нм. Электроемкость мала, поэтому даже одиночный электрон существенно изменяет потенциал и коэффициент прохождения через КТ. Второй электрон не может попасть в КТ благодаря кулоновскому отталкиванию. Переход электрона через КТ за счет туннельного эффекта является основой одноэлектронного транзистора.

При увеличении энергии КТ, когда она переходит через очередной уровень , происходит увеличение числа состояний N() на величину, равную кратности вырождения уровня, тогда

,

где Н – функция Хевисайда. Используя (3.3) , находим плотность состояний КТ:

. (П.8.7)

8.7. Найти плотность состояний фотонного газа в объеме V.

Теория относительности допускает у частицы, движущейся со скоростью света, две проекции спина – по и против скорости, поэтому электромагнитные волны поперечные и имеют две независимые поляризации, тогда , . Излучение в объеме V, распространяющееся по всем направлениям с модулем импульса в интервале , занимает фазовый объем

,

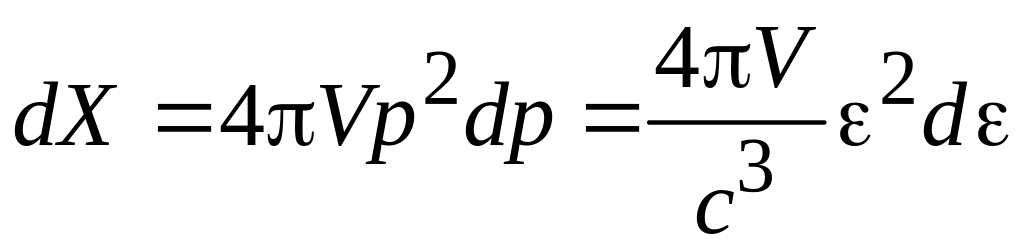где учтено . Используя , из (3.4) находим в бесконечно малых интервалах энергии и частоты число состояний

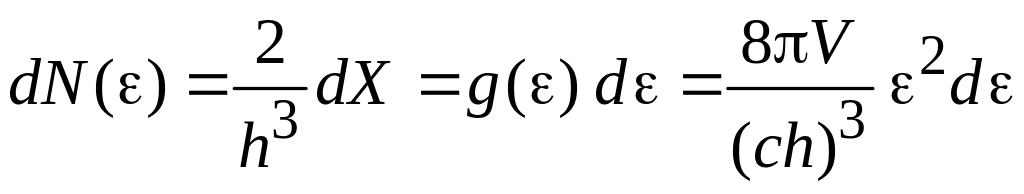, (П.8.9)

. (П.8.9а)

8. Найти плотность состояний фононного газа в модели Дебая для атомного кристалла.

Существует три типа поляризации упругих акустических волн в кристалле – два поперечных и один продольный. Для волновых колебаний атомов кристалла фононы являются квантами с энергией . Связь импульса фонона с энергией зависит от типа кристалла и интервала частот. В модели Дебая для акустической ветви спектра упругих колебаний импульс фонона аналогично импульсу фотона линейно зависит от частоты

,

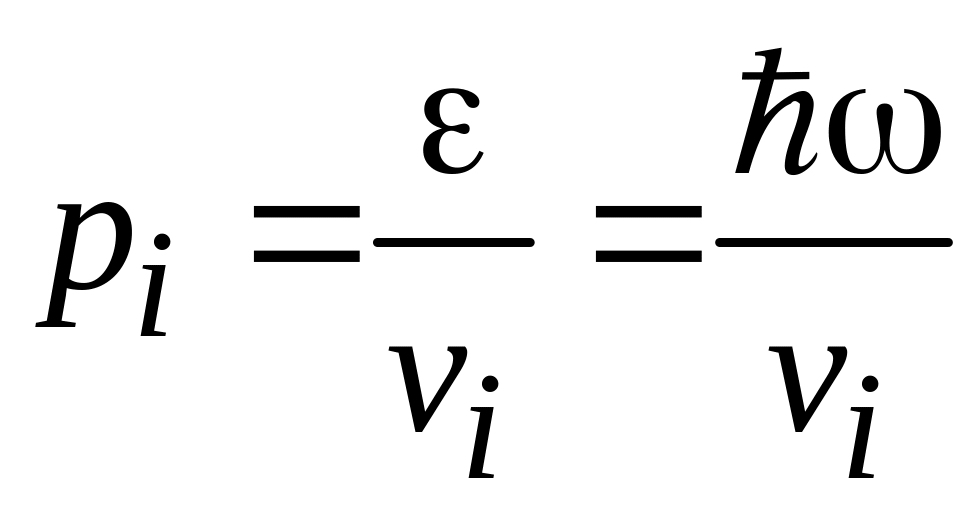где скорость v_i и импульс р_i зависят от типа поляризации волны i. Для продольных волн полагаем

, , ,

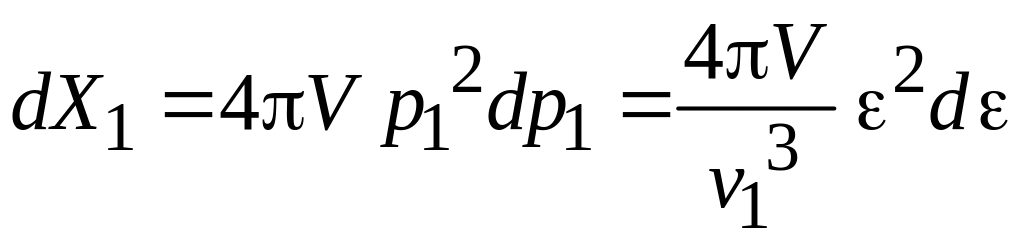и из (3.3), (3.4) получаем

,

.

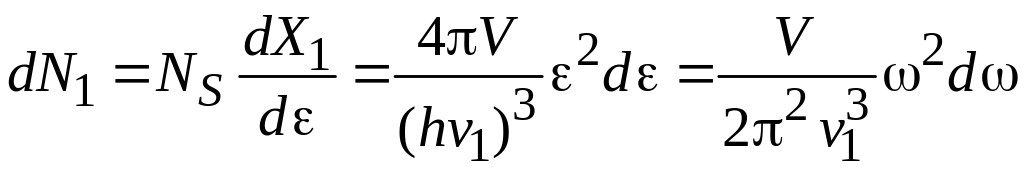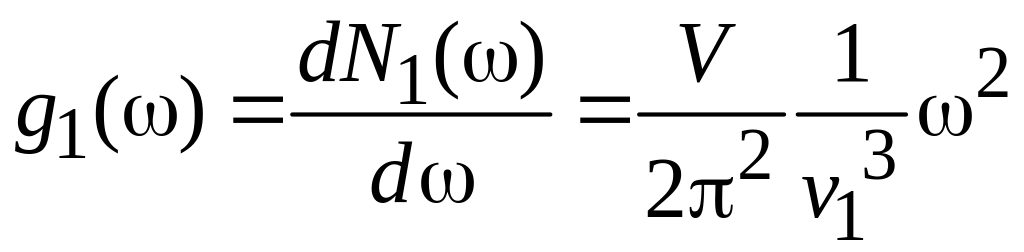Аналогичные выражения получаем для поперечных волн . Результирующая плотность состояний равна

.

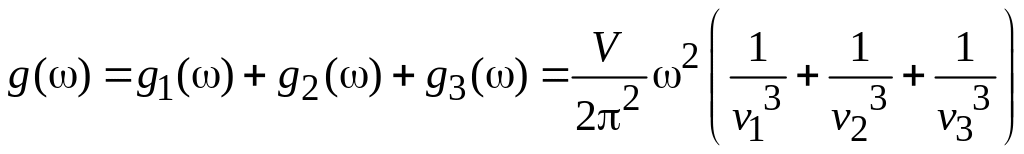Вводя среднюю скорость звука

,

получаем плотность состояний и число состояний в бесконечно малом интервале частоты

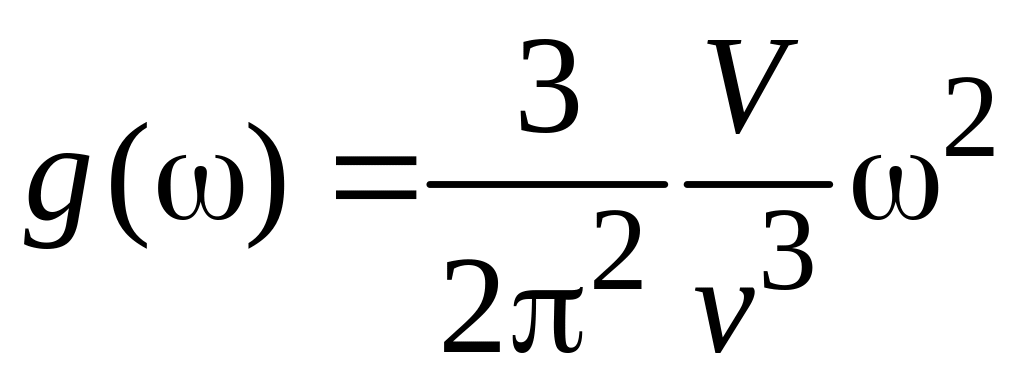, (П.8.10)

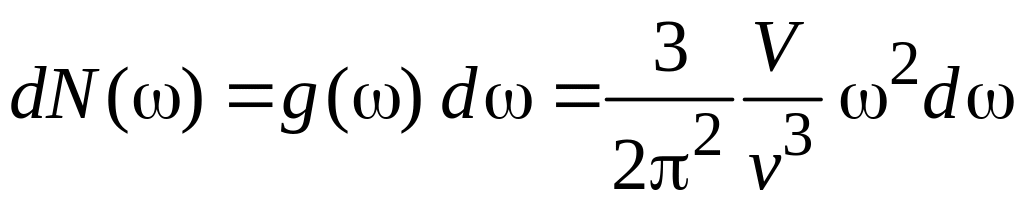. (П.8.11)