
- •Лекция 13
- •1. Решение произвольных систем линейных уравнений.
- •2. Решение однородных систем.
- •3. Понятие линейного пространства.
- •4. Примеры линейных пространств.
- •5. Евклидово пространство.
- •6. Базис линейного пространства.
- •7. Линейные преобразования.
- •8. Матрица линейного преобразования.
- •9. Собственные векторы и собственные числа.
7. Линейные преобразования.
Опр.
Говорят,
что в векторном пространстве L задан
оператор
![]() или преобразование
,
если каждому вектору
поставлен в соответствие вектор
или преобразование
,
если каждому вектору
поставлен в соответствие вектор
![]() .
.
Опр.
Оператор
или преобразование
,
называется линейным, если для
![]() и числа
и числа
![]() выполняется условие:
выполняется условие:
1.
![]()
2.
![]() .
.
Вектор
называется
образом
вектора
![]() .
Вектор
- называется прообразом
вектора
.
Вектор
- называется прообразом
вектора
![]() .
.
Замечание: Линейное преобразование называется линейным оператором , а также линейным отображением.
Геометрический смысл свойств.
Свойство
1 – означает, что диагональ параллелограмма,
построенного на векторах
![]() отображается
в диагональ
отображается
в диагональ
![]() параллелограмма, построенного на
векторах
параллелограмма, построенного на
векторах
![]() .
.

Свойство
2 - означает, что если вектор
увеличился в
раз то вектор
![]() тоже увеличился в
раз.
тоже увеличился в
раз.
Следовательно, при линейном отображении коллинеарные вектора переходят в коллинеарные.
Примеры линейных преобразований:
1.)
Преобразование, которое вектор
отображает в вектор
,
является линейным и называется
тождественным![]() .
.
2.)
Преобразование,
которое вектору
ставит в соответствие вектор![]() ,
является линейным. Геометрически
преобразование
,
является линейным. Геометрически
преобразование![]() представляет
собой однородное растяжение (сжатие)
всех векторов пространства. Такое
преобразование называется гомотетией.
При
=0
преобразование
называется
нулевым и обозначается
представляет
собой однородное растяжение (сжатие)
всех векторов пространства. Такое
преобразование называется гомотетией.
При
=0
преобразование
называется
нулевым и обозначается
![]() .
.
8. Матрица линейного преобразования.
Пусть
в линейном пространстве L
задан базис
![]() ,
,
![]() ,
…,
,
…,![]() .
Тогда любой вектор
.
Тогда любой вектор
![]() можно
представить
можно
представить
![]() . Пусть в нашем пространстве задан
линейный оператор
. Пусть в нашем пространстве задан
линейный оператор
![]() .
Можно показать, что матрица оператора
в базисе
,
,
…,
есть
.
Можно показать, что матрица оператора
в базисе
,
,
…,
есть
![]() .
.
Найдем
![]() .
.
![]()
 (1)
(1)
Разложение
вектора
![]() по
базису
по
базису
![]() будет
иметь вид
будет
иметь вид
![]() .
Придавая i
значения i=1,2,…,n,
запишем разложение векторов
.
Придавая i
значения i=1,2,…,n,
запишем разложение векторов

![]() …
…![]() по
базису
по
базису
![]() ,
,
![]() ,
…,
,
…,![]() .
.

![]() (2)
(2)
…………………………………………..
![]()
Пусть
вектор
![]() в базисе
,
,
…,
имеет
координаты
в базисе
,
,
…,
имеет
координаты
![]() ,
то есть
,
то есть
![]() (3).
(3).
Подставим (2) и (3) в (1) получим:

Соберем
подобные при
,
,
…,
,
получим
![]()
![]() (4)
(4)
Дает
связь между координатами вектора
и
![]() .
.
 это
матрица линейного оператора
в базисе
,
,
…,
.
это
матрица линейного оператора
в базисе
,
,
…,
.
9. Собственные векторы и собственные числа.
Опр.
Пусть дано
линейное преобразование
![]() .
Не нулевой вектор
называется собственным вектором
линейного преобразования, если
,
где
- действительное число, оно называется
собственным числом или собственным
значением вектора
.
Не нулевой вектор
называется собственным вектором
линейного преобразования, если
,
где
- действительное число, оно называется
собственным числом или собственным
значением вектора
![]() .
Равенство
можно
представить в виде
.
Равенство
можно
представить в виде
![]() . (5)
. (5)
Замечание.
Определение означает, что вектор
переходит в коллинеарный вектор
![]() .
.
Найдем собственные векторы и собственные значения. Для этого рассмотрим линейное пространство R с базисом , , …, и вектор
![]() , (6)
, (6)
Матрица
линейного оператора
в базисе
![]() есть
есть
Матрица
тождественного оператора
![]() в этом же базисе
есть
в этом же базисе
есть
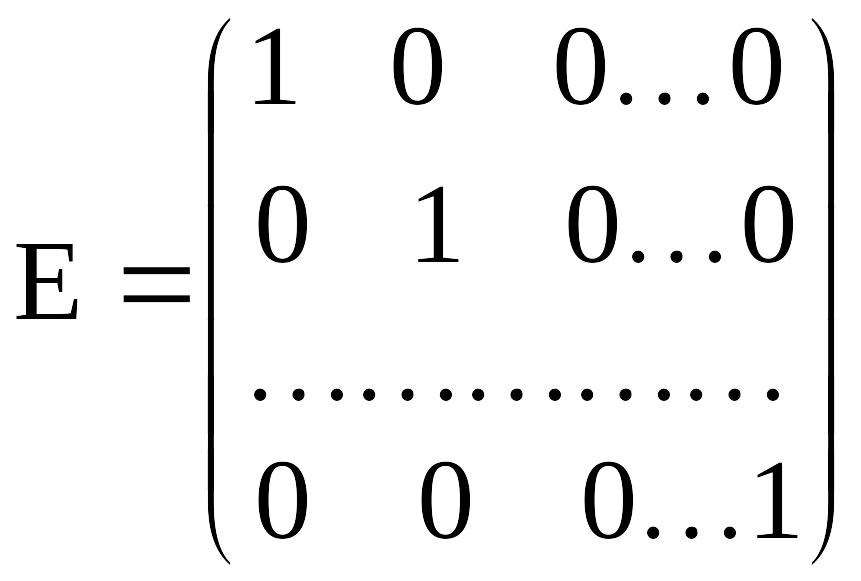 ,
так как он отображает вектор
,
так как он отображает вектор
![]() в
,
тогда запишем выражение (5) в матричном
виде:
в
,
тогда запишем выражение (5) в матричном
виде:
![]() или
или
![]() .
.
В результате получим однородную систему
![]() (7)
(7)
Однородная система, всегда совместна. Если r<n имеет не нулевые решения, что возможно при Мn=0,то есть
![]() (8)
(8)
Это
выражение называется характеристическое
уравнение. Решая его найдем собственные
числа
![]() .
Подставив их в систему (7) найдем
собственные векторы
.
Подставив их в систему (7) найдем
собственные векторы
![]() .
.
