1.10 Переходные процессы в цепи rc
Значительный практический интерес представляют нестационарные явления, возникающие при заряде и разряде емкости. Предположим, что цепь на рисунке 1.28 в момент t = 0 подключается к источнику внешнего напряжения. Запишем для этой цепи второй закон Кирхгофа в следующем виде:
uс + ur = e(t), t ³ 0. (1.110)
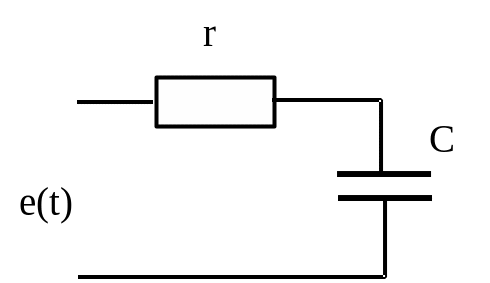
Рисунок 1.28 – Заряд ёмкости через сопротивление
Учитывая,
что ток в цепи i
= С
и ur
= ir
= rC
,
формулу (1.110)
можно записать следующим образом:
.
(1.111)
Полученное равенство представляет собой линейное дифференциальное уравнение первого порядка с неизвестной функцией uc. Общее решение уравнения можно записать в виде суммы свободной uсв и вынужденной ив составляющих напряжения:
,
(1.112)
где tц = rC – постоянная времени цепи rС.
Рассмотрим пример переходного процесса, если цепь rС подключается к источнику постоянного напряжения U0, а функция е(t) имеет вид скачка напряжения. Величина ив в этом случае должна быть равна внешнему напряжению U0, так как при t ® µ емкость заряжается до напряжения источника питания. Следовательно,
.
(1.113)
Для определения постоянной интегрирования А введем начальные условия. Будем иметь uc(0+) = uc(0–) = 0, откуда вытекает, что А = –U0. Таким образом, при t ³ 0:
;
.
(1.114,
1.115)
Из последнего выражения видно, что напряжение на емкости в процессе заряда возрастает по экспоненциаль ному закону, стремясь к величине U0 (рисунок 1.29).
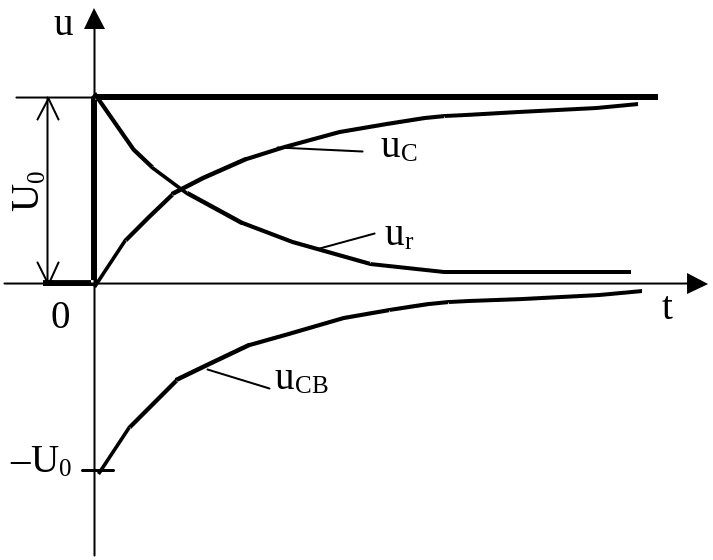
Рисунок 1.29 – Переходной процесс в rC цепи
при включении постоянного напряжения
Скорость заряда ем кости зависит от постоянной временя цепи: чем больше величина емкости и активного сопротивления, определяющих tЦ, тем медленнее растет напряжение uc. Ток
(1.116)
с течением времени убывает по экспоненте. Аналогично изменяется и напряжение на активном сопротивлении:
.
(1.117)
Если напряжение на емкости к моменту включения равно Uн, начальные условия должны быть записаны в виде: Uc (0+) = Uc(0–) = Uн . В этом случае напряжение uc определяется формулой
.
(1.118)
1.10.1 Операторный метод расчета переходных процессов
В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:
p = a + jw. (1.119)
При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике. Символический метод, рассмотренный ранее, является частным случаем данного при а = 0.
Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением
,
(1.120)
где f(t) – функция действительного переменного t, определенная при t³0 (при t<0, f(t) = 0) и удовлетворяющая условиям ограниченного роста:
,
(1.121)
где множитель М и показатель роста С0 – положительные действительные числа.
Обратное преобразование Лапласа определяют из решения (1.120):
,
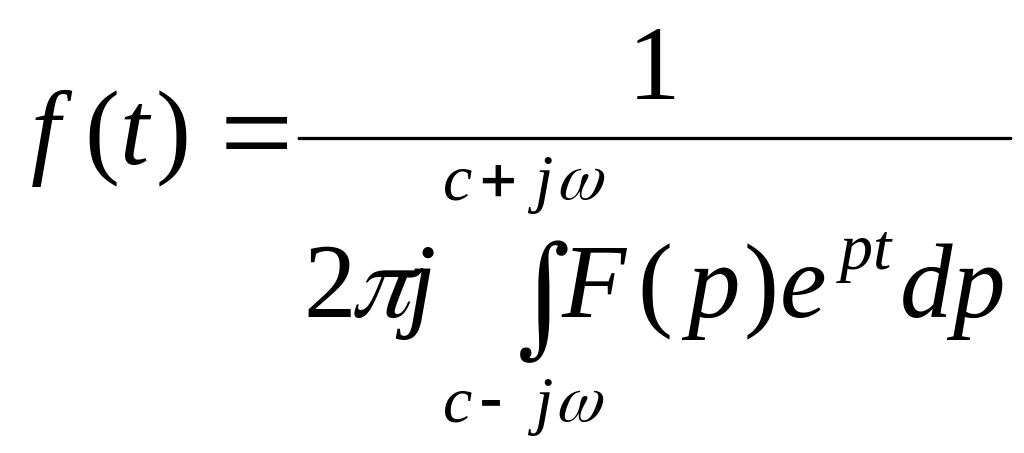(1.122)
где с – константа из решения (1.120).
Функция F(p), определяемая уравнением (1.120), носит название изображения по Лапласу, а функция f(t) в (1.122) – оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного f(t) и комплексного F(p) переменного, связанных преобразованием Лапласа.
Для сокращенной записи преобразований, используют следующую символику:
f(t) ≑ F(p) ; f(t) ⇆ F(p) ; F(p) = L[f(t)] , где L – оператор Лапласа.
Доказана для F(p) справедливость ряда теорем:
1) линейности
≑
;
(1.123)
2) дифференцирования оригинала для ненулевых начальных условий:
f'(t) ≑ pF(p) – f(0_); (1.124)
для нулевых начальных условий: f'(t) ≑ pF(p); f"(t) ≑ p2F(p), и т. д.
3)
интегрирование оригинала
≑
.
(1.125)
Имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций.