4.3. Метод Зейделя

Рассмотрим на примере линейной САУ (4.1) обозначив

(4.7)

здесь c=-b .Метод Зейделя состоит в поэлементном нахождении , но с учетом уже вычисленных значений .

Предположим, что все диагональные элементы матрицы A не равны нулю и известен вектор (при m =0,

-вектор начальных приближений). Запишем первое уравнение системы (4.7) в виде

откуда легко определить '. Величину находим из второго уравнения с учетом известного

В результате для каждого

Представим матрицу A в виде суммы трех матриц: u - строго верхнетреугольная матрица, составленная из элементов матрицы A лежащих выше главной диагонали; ; L - строго нижнетреугольная матрица, составленная из элементов матрицы A , лежащих ниже главной диагонали. Тогда последняя система уравнений в векторно-матричной форме примет вид

откуда получим решение на шаге ( m+1 )

Или после простых преобразований

(4.8)

Характеристики метода.

1) Сходимость. Итерационный процесс (4.8) сходится при выполнении следующих условий

(4.9)

т.е. матрица A должна иметь доминирующую главную диагональ. Если это условие не выполняется для исходной матрицы A , то систему (4.1) преобразуют путем умножения ее левой и правой частей на

и получают новую систему

Здесь матрица является симметричной и положительно опре­деленной и, следовательно, для нее соблюдаются сформулированные выше условия сходимости.

2)Выбор начального приближения осуществляется произвольно, так как условия сходимости (4.9) выполняются при любом .

3)Скорость сходимости - линейная.

Критерии окончания итераций описаны в подразделе 3.1.

4.4. Метод наискорейшего спуска

Здесь исходная задача решения линейной системы АУ (4.7) сводится к поиску экстремума функции

Ввиду того, что функция нулевой экстремум функции находится также в точке . Пусть на­чальное значение вектора . Движение к точке экстремума начинаем вдоль антиградиента функции в точке . Затем через некоторый интервал значение антиградиента пересчитывается для точки и т.д. до тех пор, пока не придем в точку экстремума . Алгоритм метода имеет вид

;

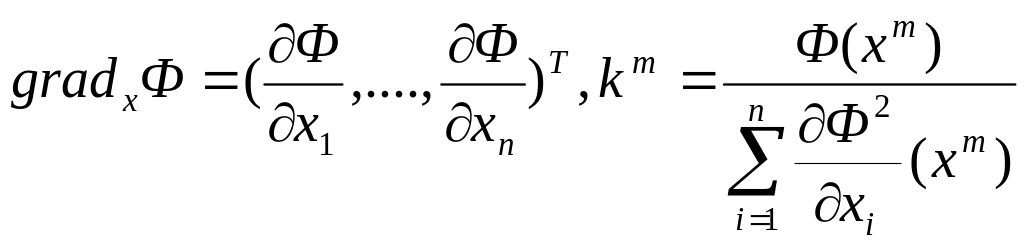(4.10)

О чевидно, что величина определяет “время” движения вдоль антиградиента функции вместе они определяют величину

Геометрическая интерпретация метода дана на рис.4.1,

Вблизи точки возможны незатухаю­щие колебания из-за

ошибок ок­ругления, которые всегда при­сутствуют. Характер и

амплиту­да колебаний зависят также от вида функции

которая для нелинейных F(х) может иметь сложный характер

поведе­ния. В том числе - может быть не единственным вектором,

дос­тавляющим экстремум функции . Это значит, что выбор

надо производить для нелинейных F (x) достаточно близко к точке .

Условием локальной сходимости алгоритма (4.10) является, как

обычно,

,

где - матрица Якоби для изображающей функции . Условии должно выполняться в каждой точке итерационного процесса (4.10). Скорость сходимости - линейная.

Для линейной функции F(x) характеристики метода, следующие.

1) Сходимость. Условия сходимости - матрица А должна быть симметричной и положительно определенной. Критерием положитель­ной определенности матрицы A является критерий Сильвестра, сог­ласно которому все главные диагональные миноры матрицы A должны быть больше 0:

(4.11)

Если эти условия не соблюдаются для исходной матрицы A , то при­меняется то же преобразование что и в методе Зейделя.

2)Выбор начального приближения . Вектор может быть любым, так как условия сходимости (4.11) не зависят от x.

3) Скорость сходимости - линейная.

4) Критерий окончания итераций описан в подразделе 3.1.