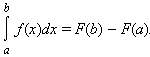Формула Ньютона – Лейбница

Е сли функция f (x) интегрируема на [a; b], то для любого существует интеграл

который называется интегралом с переменным верхним пределом.

Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.

Если функция f интегрируема на [a; b] и непрерывна в то функция F (x) дифференцируема в причем

Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида

где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

П усть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

Несобственные интегралы 1-2 рода

При вычислении определенных интегралов

предполагается, что пределы интегрирования a и b конечны, а подинтегральная функция f(x) непрерывна на отрезке интегрирования [a; b]. Если хотя бы одно из этих условий не выполняется, то определенный интеграл называют несобственным интегралом. Несобственные интегралы бывают двух типов.

Во-первых, это несобственный интеграл 1-го рода (определенный интеграл, в котором один или оба предела интегрирования бесконечны). Его легко узнать по внешнему виду:

Во-вторых, это несобственный интеграл 2-го рода (определенный интеграл, в котором подинтегральная функция f (x) имеет одну или несколько точек разрыва на отрезке [a;b] ). Внешне он ничем не отличается от обычного определенного интеграла. Несобственные интегралы могут быть сходящимися либо расходящимися.

Несобственные интегралы 2-го рода 1

Рассмотрим теперь случай, когда промежуток интегрирования конечен, но подынтегральная функция не ограничена на нем. Строение таких функций может быть очень сложным. Мы ограничимся рассмотрением случая, когда можно указать конечное множество особых точек , таких, что в сколь угодно малых окрестностях этих точек функция не ограничена, но после удаления этих окрестностей получаем промежутки, на которых функция интегрируема.

Сначала изучим случай, когда множество особых точек состоит лишь из точки . В этом случае не ограничена на всем отрезке , но интегрируема на любом из отрезков (рис. 19). За значение интеграла естественно принять предел , если этот предел существует.

Введем следующее определение:

Пусть функция не ограничена на отрезке , но интегрируема на любом из отрезков , где . Несобственный интеграл называют сходящимся, если существует предел . Значение этого предела и называют значением интеграла . Если же этот предел не существует, то интеграл называют расходящимся.