Сложное сопротивление

До сих пор мы рассматриваем задачи, где стержни конструкции испытывали одну из простейших деформаций: осевое растяжение или сжатие, кручение, плоский изгиб. На практике большинство элементов машин и конструкций подвергается действию сил, вызывающих одновременно не одну из рассмотренных деформаций, а две и более. Такие случаи сопротивления стержней, когда имеются комбинации простейших деформаций, называют сложным сопротивлением.

При расчетах на сложное сопротивление исходят из так называемого принципа независимости действия сил, то есть предполагают, что влиянием деформаций, вызванных одной из приложенных к упругой системе нагрузок на результаты действия остальных нагрузок, можно пренебречь.

Виды сложного сопротивления

Косой изгиб. Косым изгибом называют такой изгиб бруса, при котором силовая плоскость не совпадает ни с одной из главных плоскостей.

Косой изгиб, вызванный силами, лежащими в одной силовой плоскости, называется плоским косым изгибом. Если же при косом изгибе силы действующие на брус не лежат в одной плоскости, то брус будет испытывать пространственный косой изгиб.

Рассмотрим пример плоского косого изгиба бруса прямоугольного сечения. Разложим силу F на две составляющие F_z=Fcos и F_y=Fcos.

Каждая составляющая силы F вызовет прямой изгиб: F_z относительно оси y, F_y относительно – z. Следовательно, косой изгиб можно рассматривать как сумму двух прямых изгибов в двух взаимно перпендикулярных плоскостях.

Тогда изгибающие моменты в некотором произвольном сечении, находящиеся на расстоянии x от края будут равны:

,	(7.8)
.

Условие прочности можно записать в виде:

.

(7.9)

С овместное действие изгиба и растяжения или сжатия.

На практике очень часто встречаются случаи совместной работы стержня на изгиб и на растяжение или сжатие.

Пусть на балку AB действуют равномерно распределённая нагрузка q и продольно сжимающая сила F.

Применяя способ сложения действия сил, можно найти нормальное напряжение в любой точке каждого поперечного сечения балки, как алгебраическую сумму напряжений, вызванных силами F и q.

Сжимающие напряжения _сж от силы F равномерно распределены по площади S поперечного сечения и одинаковы для всех сечений: .

Н ормальные напряжения от изгиба в вертикальной плоскости в сечении с абсциссой x, выражаются формулой:

,

где .

Условие прочности при совместном действии изгиба и растяжения будет иметь вид:

.

(7.10)

Внецентренное сжатие или растяжение

Этот вид сложного сопротивления вызывается одними продольными силами.

Рассмотрим нагружения бруса внецентренной нагрузкой. Рассмотрев равновесие отсеченной части бруса можно увидеть, что брус испытывает растяжение совместно с двумя изгибами. Нормальные напряжения растяжения от силы F в любой точке равны .

Нормальные напряжения, вызываемые изгибами относительно осей y и z можно определить как

, .

Тогда условие прочности примет вид:

(7.11)

С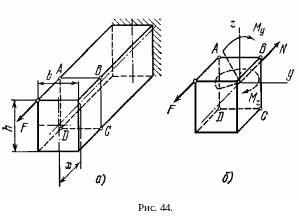 овместное действие изгиба и кручения. На практике часто встречаются детали, работающие на совместное действие кручения и изгиба.

При расчете элементов, работающих одновременно на изгиб и кручение, в первую очередь надо выяснить расчетные значения изгибающихся M_и и крутящих M_x моментов.

Рассмотрим прямой вал круглого поперечного сечения, к которому в сечениях а-а и с-с приложены внешние крутящие моменты, а в сечении b-b внешняя сосредоточенная сила F. Для того, чтобы определить нормальные напряжения изгиба, возникающие в сечениях вала от действия силы F, необходимо определить реакции опор А и В. Для данного случая . Составим уравнения и построим эпюры внутреннего изгибающего момента для I и II участков вала (рис. 45):

, при ;

, при .

Внутренний крутящий момент действует только между сечениями а-а и с-с и равен внешнему крутящему моменту M_x=T.

В поперечных сечениях вала действуют нормальные напряжения и касательные напряжения .

Т огда получим следующие условия прочности по четырём теориям прочности:

теория набольших нормальных напряжений:

;

(7.12)

теория набольших удлинений:

;

(7.13)

теория набольших касательных напряжений:

;

(7.14)

теория потенциальной энергии формоизменения:

.

(7.15)

Для проектного расчета удобно воспользоваться формулой:

,

(7.16)

где М_расч - расчетный момент, величина которого зависит как от M_и и M_x, так и от принятой теории прочности.

По теории набольших нормальных напряжений:

;

(7.17)

по теории набольших удлинений:

;

(7.18)

по теории набольших касательных напряжений:

;

(7.19)

по теории потенциальной энергии формоизменения:

.

(7.20)

Формула (6.9) по своей структуре совершенно совпадает с обычной формулой (4.14) проверки прочности по нормальным напряжениям при изгибе моментом М_расч. Тогда из условия прочности:

или .

Для того, чтобы воспользоваться этой формулой остается установить, какой из теорий прочности следует воспользоваться, то есть по какой из приведённых выше формул вычислять расчетный момент.

Исходя из того, что валы, как правило, изготавливаются из низкоуглеродистых или среднеуглеродистых сталей и других, как правило, пластичных материалов, то при выборе теории прочности обычно применяют третью или четвёртую теорию.