2.2. Обратные преобразования

Преобразование M₀₁ установили как преобразование, переводящее точку A из положения A₀ в положение A₁. Теперь будем интересоваться вопросом: если известна M₀₁, то какова будет матрица преобразования, переводящая точку A из положения A₁ в положение A₀. Такую матрицу естественно назвать M₁₀.

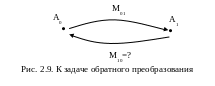
A₁ = M₀₁A₀, M₀₁ – задано. Найти M₁₀, переводящую точку A из положения A₁ в положение A₀, т.е. такую, при которой A₀ = M₁₀A₁.

Ответ на этот вопрос дают элементарные свойства матричных уравнений. Разрешим уравнение относительно A₀. Получим: , где есть матрица, обратная . В итоге:

; ; ; ; ; .(2.8)

Все соотношения, перечисленные в (2.8), справедливы.

Напомним общий прием нахождения обратной матрицы. Пусть задана матрица B, найти матрицу С, обратную B, т.е. C = B^–1. Тогда элементы c_ij матрицы С будут находиться по формуле

,

где B_ij – алгебраическое дополнение элемента b_ij матрицы B; detB – определитель матрицы B. Алгебраическое дополнение B_ij = (–1)^i+j – определитель, полученный при удалении из матрицы B i-й строки и j-го столбца, нумерация строк и столбцов с единицы. Обратная матрица существует, если .

Полезно знать матрицы, обратные тем элементарным, которые ранее были определены:

.

Для приведенной цепочки преобразований справедливы такие соотношения:

; ; ;

; ; .

Аналоги формул (2.6) и (2.7):

A₀ = M₁₀M₂₁M₃₂  M_N(N–1)A_N =M_N0; (2.9)

M_N0 = M₁₀M₂₁M₃₂  M_N(N–1). (2.10)

2.3. Аффинные преобразования

Разговор о преобразованиях был начат с формул (2.1). Формула (2.5) это то же, что и (2.1), только записанное в компактной матричной форме.

Преобразования (2.1) называют аффинными преобразованиями. Они обладают рядом полезных свойств, обусловивших их широкое применение в графике:

1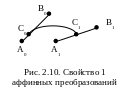 . Отрезок прямой преобразуется в отрезок прямой. Это означает следующее: если в результате преобразований точка A₀ переходит в A₁, а B₀ в B₁, то и любая точка C₀ на A₀B₀ перейдет в точку C₁ на отрезке A₁B₁, если к ней применить те же преобразования (рис. 2.10)

2. Параллельные преобразуются в параллельные. Это означает, что если A₀B₀ и C₀D₀ параллельны, то в результате применения к ним одних и тех же преобразований новые отрезки A₁B₁ и C₁D₁ будут так же параллельны (рис. 2.11).

3 . Относительные пропорции сохраняются. Это означает, что если отрезок A₀C₀ составляет, например, отрезка A₀B₀, то и отрезок A₁C₁ будет в той же пропорции к отрезку A₁B₁ (рис. 2.12).

4. Если преобразованию M подвергнут замкнутый выпуклый многоугольник, то

.

5. В результате последовательности аффинных преобразований получаются аффинные преобразования.

6. Любое аффинное преобразование может быть разложено (представлено как последовательность) на элементарные, ранее рассмотренные.

А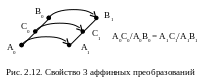 ффинные преобразования удобны тем, что, если геометрический объект аппроксимирован отрезками прямых или плоскими гранями, то для того, чтобы выполнить заданные преобразования объекта, достаточно выполнить эти преобразования над всеми узловыми точками.