3. Операции в римской символике

Римские цифры — цифры, использовавшиеся древними римлянами в своей непозиционной системе счисления.

Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.

римские цифры1 I лат. unus

5 V лат. quinque

10 X лат. decem

50 L лат. quinquaginta

100 C лат. centum

500 D лат. quingenti

1000 M лат. mille

В русском языке для закрепления в памяти буквенных обозначений цифр в порядке убывания существуют мнемонические правила:

Мы Dарим Сочные Lимоны, Хватит Vсем Iх.

Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам

Соответственно M, D, C, L, X, V, I.

Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.

При этом некоторые из цифр (I, X, C, M) могут повторяться, но не желательно более трех раз, таким образом с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX). В ранние периоды существовали знаки для обозначения бо́льших цифр — 5000, 10 000, 50 000 и 100 000[источник не указан 505 дней] (тогда максимальное число по упомянутому правилу равно 399 999). При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается как CCLXXXIII, то есть 200+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза.

Пример: число 1988. Одна тысяча M, девять сотен CM, восемь десятков LXXX, восемь единиц VIII. Запишем их вместе: MCMLXXXVIII.

Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту: LXIV. Иногда черту рисовали и сверху, и снизу: XXXII — в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности). У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: VM = 6000.

Часы марки Tissot с традиционным написанием «IIII»

Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII».

Меньшая цифра может быть записана и слева от большей, тогда её следует вычесть из большей. В этом случае повторения меньшей цифры не допускаются. По-римски число 94 будет XCIV=100-10+5-1=94 — так называемое «правило вычитания» (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 — как XXXX). Существует шесть вариантов использования «правила вычитания»:

IV = 4

IX = 9

XL = 40

XC = 90

CD = 400

CM = 900

Необходимо отметить, что другие способы «вычитания» не допустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел: например, в программе Microsoft Excel при преобразовании арабских цифр в римские при помощи функции «РИМСКОЕ()» можно использовать несколько видов представления чисел, от классического до сильно упрощенного (так, число 499 может быть записано как CDXCIX, LDVLIV, XDIX, VDIV или ID). Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:

999. Тысяча (M), вычтем 1 (I), получим 999 (IM) вместо CMXCIX. Следствие: 1999 — MIM вместо MCMXCIX

95. Сто (C), вычтем 5 (V), получим 95 (VC) вместо XCV

1950: Тысяча (M), вычтем 50 (L), получим 950 (LM). Следствие: 1950 — MLM вместо MCML

С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Например, число 123123 будет выглядеть так:

CXXIIICXXIII

Римские цифры появились за 500 лет до нашей

Римские цифры, цифры древних римлян. Система Р. ц. основана на употреблении особых знаков для десятичных разрядов I = 1, Х =10, С = 100, М = 1000 и их половин V = 5, L = 50, D = 500. Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая - перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400. Например, VI = 5+1 = 6,IV = 5 - 1 = 4 (вместо IIII). XIX = 10 + 10 - 1 = 19 (вместо XVIIII), XL = 50 - 10 =40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д. Выполнение арифметических действий над многозначными числами в этой записи весьма неудобно. Система Р. ц. в настоящее время не применяется, за исключением, в отдельных случаях, обозначения веков (XV век и т.д.), годов н. э. (MCMLXXVII т. д.) и месяцев при указании дат (например, 1. V.1975), порядковых числительных, а также иногда производных небольших порядков, больших трёх: yIV, yV и т.д.

I 1 VIII 8 LXXV 75 D 500

II 2 IX 9 XCII 92 DCXCV 695

III 3 X 10 IC 99 DCCIL 749

IV 4 XVIII 18 C 100 M 1000

V 5 XXXI 31 CCCII 302 MCMIX 1909

VI 6 XLVI 46 CDXLI 441 MCMLXXXIV 1984

VII 7 L 50 ID 499 MIM 1999

VArt (ответ на возникавший ранее вопрос): Отсюда понятно, что во избежание 4-х кратного повторения максимально возможное число здесь - 3999, т.е. MMMIM.

Двоичная система0 0 111 7 1110 14 10101 21

1 1 1000 8 1111 15 10110 22

10 2 1001 9 10000 16 100000 32

11 3 1010 10 10001 17 1000000 64

100 4 1011 11 10010 18 1100100 100

101 5 1100 12 10011 19 10000000 128

110 6 1101 13 10100 20 100000000 256

4. Бином Ньютона.

Комбинаторика. Бином Ньютона

Общим термином «соединения» мы будем называть три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.).

Перестановки. Возьмём  n различных элементов:  a₁ , a₂ , a₃ , …, a_n . Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называетсяперестановкой. Общее количество перестановок из n элементов обозначается P_n . Это число равно произведению всех целых чисел от 1 до n :

 

Символ  n!  ( называется факториал ) - сокращённая запись произведения:  1 · 2 · 3 ·  … · ( n – 1 ) · n .

 

П р и м е р .  Найти число перестановок из трёх элементов:  a, b, c.

Р е ш е н и е .  В соответствии с приведенной формулой:  P₃ = 1 · 2 · 3 = 6.                          Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.

Размещения.  Будем составлять группы из  m различных элементов, взятых из множества, состоящего из  n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются  размещениями из  n элементов по m .

Их общее количество обозначается:    и равно произведению:

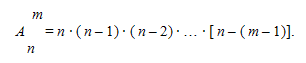
П р и м е р .  Найти число размещений из четырёх элементов  a, b, c, d по два.

Р е ш е н и е .  В соответствии с формулой получим:

                         Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

Сочетания.  Будем составлять группы из  m различных элементов, взятых из множества, состоящего из  n элементов, не принимая во внимание порядок расположения этих m элементов. Тогда мы получим сочетания из  n элементов по  m .

Их общее количество обозначается     и может быть вычислено по формуле:

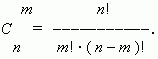
Из этой формулы ясно, что

 

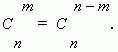
Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все  n элементов. Формула числа сочетаний даёт это значение, если только принять, что  0! = 1,  что является определением  0! .

В соответствии с этим определением получим:

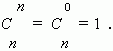
Общее число сочетаний можно вычислить, пользуясь и другим выражением:

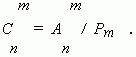
П р и м е р . Найти число сочетаний из пяти элементов:  a, b, c, d, e  по три.

Р е ш е н и е :

                             

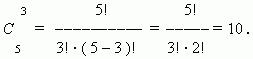
                        Эти сочетания:  abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Бином Ньютона. Это формула, представляющая выражение ( a + b ) ⁿ  при положительном целом  n  в виде многочлена:

            

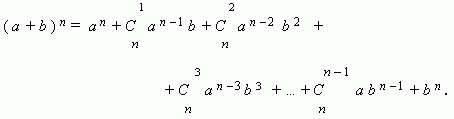
Заметим, что сумма показателей степеней для  a  и  b  постоянна и равна n.

П р и м е р  1 .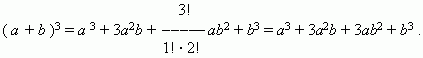 

                          ( См. формулу куба суммы двух чисел ).

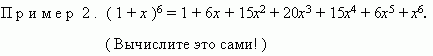
Числа      называются биномиальными коэффициентами.

Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

Первая строка в этой таблице содержит биномиальные коэффициенты для  n = 1;  вторая - для  n = 2;  третья - для   n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:

( a + b )⁷ , 

мы можем получить результат моментально, используя таблицу:

Свойства биномиальных коэффициентов.                                                                                                

 1.  Сумма коэффициентов разложения ( a + b ) ⁿ  равна  2 ⁿ .

Для доказательства достаточно положить  a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения:

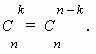
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна

Для доказательства воспользуемся биномом:   Здесь чётные члены имеют знак  « + » , а нечётные - «  ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов   равны между собой, поэтому каждая из них равна:    что и требовалось доказать.

Рациональные неравенства.

Пусть ((() ( числовая функция одного или нескольких переменных

(аргументов). Решить неравенство ((() < 0 (((() > 0) (1) ( это значит найти все значения аргумента (аргументов) функции (, при которых неравенство (1) справедливо. Множество всех значении аргумента

(аргументов) функции (, при которых неравенство (1) справедливо, называется множеством решении неравенства или просто решением неравенства. Множество решении нестрого неравенства ((() ( 0 (((() ( 0) (2)

представляет собой объединение множества решении неравенства (1) и множества решении уравнения ((() = 0.

Два неравенства считаются эквивалентными, если множества их решении совпадают.

Под множеством допустимых значении неизвестных, входящих в неравенство, понимают область определения функции (((). Неравенства вида (1) или (2), составленные для различных функций, могут быть сведены в систему неравенств. Решить систему неравенств (это значит найти множество всех значении аргументов функции (i((), при которых справедливы все неравенства системы одновременно.

Говорят, что системы неравенств эквивалентны, если множества их решении совпадают.

Свойства равносильных неравенств.

При решении неравенств используют свойства равносильности.

Неравенства с одной переменной называются равносильными, если множества их решении совпадают.

Например, неравенства 3х > 6 и х – 2 > 0 имеют одинаковые множества решении х([2; +(]. Эти неравенства – равносильные. Неравенства х > 0 и х2 > 0 – неравносильные, так как решение первого неравенства есть множество х([0; +(], а решение второго неравенства есть множество х([-(; 0]([0; +(]. Эти множества не совпадают.

При решении неравенств выполняются только такие преобразования, при которых получаются более простые равносильные неравенства. Эти преобразования возможны при выполнении следующих свойств равносильных

неравенств.

Свойство 1. Если к обеим частям неравенства прибавить одно и то же число или одно и то же выражение, которое имеет смысл при всех значениях переменной, то получим неравенство, равносильное данному.

Дано. Р(х) > Q(x) – неравенство, Т(х) – выражение, которое имеет

смысл при всех действительных значениях х, х(R.

Доказать. Неравенства Р(х) > Q(x) и Р(х) + Т(х) > Q(x) + T(x) –

равносильные.

Доказательство. а) Пусть при х = а неравенство Р(а) > Q(a) – верное

числовое равенство, т.е. х =а – одно из решении неравенства Р(х) > Q(x),

Т(а) – значение Т(х) при х =а.

По свойству числовых неравенств Р(а) + Т(а) > Q(a) + T(a) – верное

числовое неравенство.

Следовательно, х = а – одно из решений неравенства Р(х) + Т(х) > Q(x)

+ T(x). Поэтому, если х =а есть решение первого неравенства, то это

значение есть также решение второго неравенства.

б) Пусть х = b – одно из решений неравенства Р(х) + Т(х) > Q(x) +

T(x), т.е. P(b) + T(b) > Q(b) + T(b) –верное числовое неравенство. По

свойству числовых неравенств P(b) > Q(b) – тоже верное числовое

неравенство. Следовательно, х = b – решение неравенства P(x) > Q(x).

Так как множества решений неравенства P(x) > Q(x) и P(x) + T(x) >

> Q(x) + T(x) совпадают, то эти неравенства равносильные.

Свойство 2. Если в неравенстве любое слагаемое, которое имеет смысл при вех

х(R, перенести из одно части в другую с противоположным знаком, то получим

неравенство, равносильно данному.

Дано. P(x) + T(x) > Q(x) – неравенство, Т(х) – слагаемое, которое

имеет смысл при всех х(R.

Доказать. Неравенства P(x) + T(x) > Q(x) и P(x) > Q(x) – T(x) –

равносильные.

Доказательство. По свойству 1 можно к обеим частям неравенства

P(x) + T(x) > Q(x) прибавить слагаемое (-Т(х)), так как это слагаемое имеет

смысл при всех х(R; получим равносильное неравенство:

P(x) + T(x) – T(x) > Q(x) – T(x), отсюда P(x) > Q(x) – T(x).

Свойство 3. Если обе части неравенства умножить на одно и то же

положительное число или на одно и то же выражение, положительное при всех

значениях переменной, то получим неравенство, равносильное данному.

Дано. P(x) > Q(x) – неравенство (1),

T(x) > 0, x(R,

P(x)(T(x) > Q(x)(T(x) – неравенство (2).

Доказать. Неравенства (1) и (2) равносильные.

Доказательство. Пусть при х = а P(a) > Q(a) – верное числовое

неравенство, т.е. х = а – одно из решении первого неравенства. T(a) –

значение Т(х) при х = а Т(а) > 0. По свойству числовых неравенств P(a)(T(a) > Q(a)(T(a) – тоже верное

числовое неравенство, т.е. х = а –одно из решении первого неравенства.

Следовательно, если х= а – решение первого неравенства, то х = а – также решение второго неравенства.

Пусть при х = b неравенство P(b)(T(b) > Q(b)(T(b) – верное числовое неравенство, т.е. х = b – одно из решении второго неравенства. По свойству числовых неравенств P(b) > Q(b) – тоже верное числовое неравенство, так как T(b) > 0. Следовательно, х = b – одно из решении первого неравенства. Поскольку множества решении первого и второго неравенств совпадают, то они равносильные.

Свойство 4. Если обе части неравенства умножить на одно и то же

отрицательное число или на одно и то же выражение, отрицательное при всех

значениях переменной, и изменить знак неравенства на противоположный, то

получим неравенство, равносильное данному.Это свойство доказывается аналогично 3 свойству.

Алгебраические неравенства.

Линейными (строгими и нестрогими) называются неравенства вида

ax + b > 0, ax + b < 0, ax + b ( 0, ax + b ( 0, a ( 0,

решениями которых будут:

при a > 0

x((- ; ( ), x(( -(; - ), x([ - ; ( ), x(( -(; - ],

при а < 0

x(( -(; - ), x(( - ; ( ), x(( -(; - ], x([ - ; ( ).

Квадратными (строгими и нестрогими) называются неравенства вида

ax2 + bx + c > 0, ax2 + bx + c < 0,

ax2 + bx + c ( 0, ax2 + bx + c ( 0,

где a, b, c ( некоторые действительные числа и а ( 0.

Квадратное неравенство ax2 + bx + c > 0 в зависимости от значении

своих коэффициентов a, b и c имеет решения:

при а > 0 и D = b2 – 4ac ( 0

x(( -(; ;2a ) )((;2a) ; ();

при а > 0 и D < 0 x ( любое действительное число;

при а < 0 и D ( 0

x(( ;2a) ; ;2a ) );

при а < 0 и D < 0

x = ( (т. е. решении нет ).

Решение неравенства ax2 + bx + c < 0 сводится к решению

рассмотренного неравенства, если обе части неравенства умножить на (-1).

Метод интервалов.

Пусть Рn(x) ( многочлен n-й степени с действительными коэффициентами, а c1, c2, ( , ci ( все действительные корни многочлена с кратностями k1, k2, ( , ki соответственно, причем с1 > c2 > ( > ci. Многочлен Pn(x) можно

представить в виде Рn(x) = (x - c1) k1(x - c2) k2 ( (x – ci)ki Qm(x), (3) где многочлен Qm(x) действительных корней не имеет и либо положителен, либо отрицателен при всех х(R. Положим для определенности, что Qm(x) > 0. Тогда

при х > c1 все сомножители в разложении (3) положительны и Рn(х) > 0. Если с1 ( корень нечетной кратности (k1 ( нечетное), то при х((с2; с1) все сомножители в разложении (3), за исключением первого, положительны и

Рn(х)<0. В этом случае говорят, что многочлен Рn(х) меняет знак при переходе через корень с1. Если же с1 ( корень четной кратности (k1 (четное), то все сомножители (в том числе и первый) при х((с2; с1) положительны и, следовательно, Рn(х) > 0 при х((c2; с1). В этом случае говорят, что многочлен Рn(х) не меняет знак при переходе через корень с1. Аналогичным способом, используя разложение (3), нетрудно убедится, что при переходе через корень с2 многочлен Рn(х) меняет знак, если k2 ( нечетное, и не меняет знака, если k2 ( четное. Рассмотренное свойство многочленов используется для решения неравенств методом

интервалов. Для того чтобы найти все решения Рn(х) > 0, (4)

достаточно знать все действительные корни многочлена Рn(х) их кратности и знак многочлена Рn(х) в произвольно выбранной точке, не совпадающей с корнем многочлена.

Пример: Решить неравенство х4 + 3х3 – 4х > 0.

Решение. Разложим на множители многочлен Р4(х), стоящий в левой части

неравенства (*). Вынося множитель х за скобку, получаем

Р4(х) = х(х3 + 3х2 – 4).

Второй сомножитель, представляющий собой кубический многочлен, имеет

корень х = 1. Следовательно, он может быть представлен в виде

х3 + 3х2 – 4 = (х-1)(х2 + 4х + 4) = (х-1)(х + 2) 2.

Таким образом, Р4(х) = х(х - 1)(х + 2) 2 и неравенство (*) может быть

записано в виде

х(х –1)(х + 2)2 > 0. (**)

Решим неравенство (**) методом интервалов. При х > 1 все сомножители, стоящие в левой части неравенства, положительны. Будем двигаться по оси Ох справа налево. При переходе через точку х =1 многочлен Р4(х) меняет знак и принимает отрицательные значения, так как х= 1 ( простой корень (корень кратности 1); при переходе через точку х = 0 многочлен также меняет знак и принимает положительные значения, так как х =0 ( также простой корень; при переходе через точку х = -2 многочлен знака не меняет, так как х = -2 ( корень кратности 2. Промежутки знакопостоянства многочлена Р4 (х) схематически представлены на рис 1. Используя этот

рисунок, легко выписать множество решений исходного неравенства. Ответ. х ( (-(; -2) ( (-2; 0) ( (1; ().

Пример: Решить неравенство

(х2 – 3х – 2)(х2 – 3х + 1) < 10.

Решение: Пусть х2 – 3х – 2 = y. Тогда неравенство примет вид y(y +3) < 10,

или y2 + 3y – 10 < 0, откуда (y + 5)(y – 2) < 0. Решением этого неравенства

служит интервал –5 -5, x2 – 3x + 3 > 0,

откуда

(x – 4)(x + 1) < 0,

(x + )2 + > 0.

Поскольку второе неравенство выполняется при всех х, решение этой

системы есть интервал (-1; 4).

Ответ: (-1; 4).