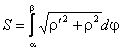12. Интеграл с переменным верхним пределом;производная по верхнему пределу

Если оставить постоянным нижний предел интегрирования a, а верхний х изменять так, чтобы x є [a; b], то величина интеграла будет изменяться. Интеграл вида:

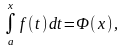x є [a; b],

называется определенным интегралом с переменным верхним пределом и является функцией верхнего предела х. Здесь для удобства переменная интегрирования обозначена буквой t, а верхний предел интегрирования – буквой х.

Теорема .Производная определенного интеграла от непрерывной функции f(x) по его переменному верхнему пределу существует и равна подынтегральной функции, в которой вместо переменной интегрирования подставлено значение верхнего предела:

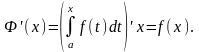
13.Формула Ньютона-Лейбница

Теорема. Если – какая–либо первообразная для непрерывной функции , то

Доказательство. Пусть –некоторая первообразная функции . Но – также первообразная для , а любые две первообразные данной функции отличаются на постоянную, то есть можно записать:

(4)

Это равенство справедливо для любых . Положим : Но , поэтому , . Полагая в (4) x=b и подставляя значение C, получим Переобозначив переменную интегрирования , получим формулу Ньютона – Лейбница:

При вычислении определенных интегралов записывать:

14.Замена переменной в определенном интеграле

Теорема. Пусть дан интеграл , где непрерывна на . Введем новую переменную , связанную с равенством . Если

2) и непрерывны на

3) при изменении z от α до β значения не выходят за пределы отрезка то

(5)

Доказательство. Пусть –первообразная для функции , то есть . Тогда по формуле Ньютона–Лейбница

(I)

покажем, что функция является первообразной для функции : : [по правилу дифференцирования сложной функции] = Тогда по формуле Ньютона–Лейбница

(II)

Сравнивая равенства (I) и (II), убеждаемся в справедливости формулы (5).

15.Интегрирование по частям в определенном интеграле

Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [ a , b ], то справедлива формула интегрирования по частям:

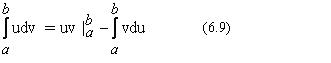
На отрезке [ a , b ] имеет место равенство (uv) /=u /v + v /u . Следовательно, функция uv есть первообразная для непрерывной функции u /v + v /u . Тогда по формуле Ньютона- Лейбница имеем

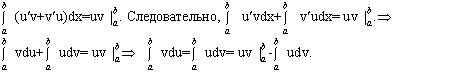
Выбор u и v осуществляется так же, как и в неопределенном интеграле.

16.Геометрические приложения определенного интеграла

Вычисление площадей плоских фигур.

  Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

 Для нахождения суммарной площади используется формула .

 Нахождение площади криволинейного сектора.

 

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид  = f(), где  - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а  - угол наклона этого радиус – вектора к полярной оси. Площадь криволинейного сектора может быть найдена по формуле

  

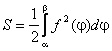
Вычисление длины дуги кривой.

 Длина ломаной линии, которая соответствует дуге, может быть найдена как .

Тогда длина дуги равна .

Из геометрических соображений:

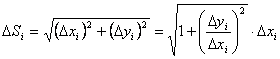
  Если задана пространственная кривая, и х = (t), у = (t) и z = Z(t), то

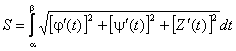
  Если кривая задана в полярных координатах, то